Расчет данных для уравнения линейной множественной регрессии

y	x	z	y2	x2	z2	xy	xz	yz
300	14,5	82	90000	210,25	6724	4350	1189	24600
350	15,0	95	122500	225,00	9025	5250	1425	33250
370	15,6	105	136900	243,36	11025	5772	1638	38850
420	17,2	120	176400	295,84	14400	7224	2064	50400
450	18,5	130	202500	342,25	16900	8325	2405	58500
500	19,3	140	250000	372,49	19600	9650	2702	70000
Σ 2390	100,1	672	978300	1689,19	77674	40571	11423	275600
My = 398,33	Mx = 16,68	Mz = 112

Вычисленные в табл. 6.5 показатели подставляем в систему уравнений (6.10):

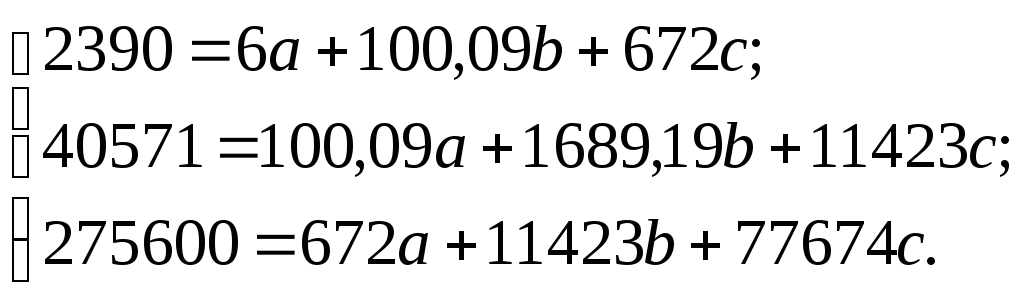
Решаем систему уравнений относительно а, b, с. Получаема = –3,26;b= 5,01;c = 2,84. Подставляем значенияа, b, с в общую формулу уравнения множественной регрессии (6.9):

y = –3,26 +5,01x + 2,84z (6.15)

Затем находим теоретические значения у'. Для этого подставляем в формулу (6.15) экспериментальные данные поxиzи заносим в табл. 6.6 для расчета критерия хи-квадрат. Поскольку χ²_ф= 0,602 < χ²_т = 11,1 приР= 0,95 для ν = 5, то можно сделать вывод, что расчет биомассы по данным температуры (х) и осадкам (z)достаточно точный.

Для определения ошибки уравнения линейной множественной регрессии показатели рассчитываем по формулам (6.12–6.14):

Σ= 978300 – 6 ∙ 398,33²= 29299,4;

Σa_ya_x =40571 – 6 ∙ 398,33 ∙ 16,68 = 706,14;

Σa_ya_z =275600 – 6 ∙ 398,33 ∙ 112 = 7922,3.

Затем подставляем полученные значения в формулу (6.11):

г/м².

Таким образом, прогнозируя урожай биомассы трав за период вегетации по температуре и осадкам, мы рискуем ошибиться в среднем на 9,35 г/м², т. е. на 2,3 %.

Таблица 6.6

Расчет данных для критерия хи-квадрат

y	у'	у – у'	(у – у')2
300	302,2	–2,26	5,11	0,017
350	341,7	8,31	69,06	0,202
370	373,1	–3,09	9,55	0,026
420	423,7	–3,71	13,76	0,032
450	458,6	–8,62	74,30	0,162
500	491	8,97	80,46	0,164
		Σ –0,4	252,241	χ2=0,603

Уравнения регрессии широко используются в научных исследованиях и в практических целях.

Глава 7 факторный анализ

7.1. Сущность и возможности применения

При изучении взаимного влияния многих процессов и явлений в последнее время все чаще обращаются к методам многомерного статистического анализа, в частности факторного анализа. Методы многомерного статистического анализа требуют применения сложной вычислительной техники.

Факторный анализ основывается на использовании статистических знаний (вычислении стандартных отклонений, знании корреляционного и регрессионного анализов). В большинстве случаев исследуется система корреляций, отраженных в корреляционной матрице. Факторный анализ представляет собой ветвь математической статистики, цель которого – разработка моделей, понятий и методов, позволяющих анализировать и интерпретировать массивы экспериментальных данных независимо от их физической природы. Анализ данных включает краткое описание распределения объектов, установление взаимоотношения процессов и явлений, отражающихся в виде параметров.

Используемый набор моделей и методов предназначен для «сжатия» информации, содержащейся в корреляционной матрице. В основе различных моделей факторного анализа лежит следующая гипотеза: параметры – это косвенные характеристики объекта или явления и представляют в совокупности тот или иной фактор. В связи с этим задача факторного анализа состоит в том, чтобы показать наблюдаемые параметры в виде линейных комбинаций факторов. Изменение фактора не всегда одинаково отражается на параметрах, поэтому среди последних могут быть выделены группы, реагирующие на каждый из факторов порознь. Параметры, входящие в одну и ту же группу, сильно коррелируют между собой; параметры, входящие в разные группы, слабо коррелируют между собой. Задача выявления факторов понимается как разбиение параметров на группы таким образом, чтобы можно было описать взаимоотношения между параметрами.

Разработано несколько вариантов факторного анализа с использованием коэффициентов только линейной корреляции (нелинейная корреляция вызывает затруднения при обработке материала). Наиболее употребительны при этом метод главных компонент, метод главных факторов и центроидный метод. Определение главных компонент и главных факторов производится с помощью ЭВМ.

Наиболее типичной формой представления данных является матрица. Это прямоугольная (или квадратная) таблица чисел, вертикальный ряд которой (столбец) обозначается индексом j, горизонтальный (строка) – индексом i. Любой элемент матрицы обозначается символом a с индексами, первый указывает номер строки, второй – номер столбца, которым соответствует данный элемент (в общем виде a_ij). Матрица обозначается прописной буквой (A, B и т. д.). О матрице, имеющей т строк и п столбцов, говорят, что ее порядок составляет т∙п. Квадратная матрица n∙п имеет порядок п. В общем виде матрица записывается следующим образом:

В факторном анализе с использованием правил матричной алгебры часто встречается операция умножения матриц. Для того чтобы умножить матрицу А на матрицу В, необходимо следующее условие: матрица A должна иметь столько столбцов, сколько строк в матрице В. Сам процесс умножения протекает по правилу «строка на столбец». Это правило означает, что каждый элемент матрицы произведения представляет собой сумму произведений элементов строки первой матрицы на соответствующие элементы столбца второй матрицы, например:

Матрица-произведение будет иметь всегда столько строк, сколько их было в первой матрице, и столько столбцов, сколько их было во второй матрице: (p ∙ q) ∙ (q ∙ r)= (p ∙ r).

Существует ряд математических методов, которые по информации, заложенной в матрице, позволяют провести классификацию объектов. Такие методы объединены в многомерный анализ, а при наличии одной строки в матрице – в одномерный анализ.

В факторном анализе используются следующие виды матриц: диагональная (в ней отличны от нуля только элементы, лежащие на главной диагонали), скалярная (все элементы диагональной матрицы равны между собой), единичная (все элементы главной диагонали равны единице), обратная (аналогична обратному числу в арифметике).

Элементами исходной матрицы в факторном анализе являются коэффициенты корреляции. В ходе анализа вычисляется также общая дисперсия σ², указывающая, в каких границах находятся значения параметров, которые характеризуют фактор. Кроме общей дисперсии в анализе учитывается факторная дисперсия (общность) и специфическая дисперсия, связанная с некоторой переменной и характеризующая только ее. Дисперсию, обусловленную ошибкой, стремятся свести к минимуму.

В итоге составляется факторная матрица. Элементы столбцов матрицы представляют собой факторные нагрузки, или коэффициенты факторного отображения, выраженные коэффициентами корреляции данной переменной с данным фактором. Таким образом, коэффициенты факторного отображения характеризуют фактор и его влияние на все параметры.

Результат факторного анализа можно также выразить в виде графика, который наглядно иллюстрирует полученные выводы. Каждую из двух связанных друг с другом переменных можно изобразить как вектор, т. е. отрезок прямой, имеющий определенную длину и направление. Величина корреляции между переменными равна произведению абсолютных величин обоих векторов на косинус угла между ними: r_1,2 = h₁h₂cos α_1,2, где r_1,2 – коэффициент корреляции; h₁– длина вектора, соответствующая первой переменной 1; h₂ – длина вектора, соответствующая переменной 2; cos α_1,2 – угол между векторами h₁ и h₂.