6.2. Гиперболическая зависимость

При проведении исследований может быть установлена нелинейная зависимость между аргументом и функцией, представляющая собой на графике кривую в виде гиперболы. Общее уравнение регрессии для гиперболической зависимости имеет вид

y = a/x + b (6.5)

где х – аргумент; у – функция; а и b – коэффициенты, величину которых следует установить.

Расчет сводится к следующему. Чтобы установить вид зависимости между функцией и аргументом, по исходным данным строится график. Затем при вычислении параметров а и b по способу координат точек подбираются две точки, расположенные на кривой или около нее по методу, описанному для линейной регрессии (см. п. 6.1). Для этих же параметров по способу наименьших квадратов используется система уравнений

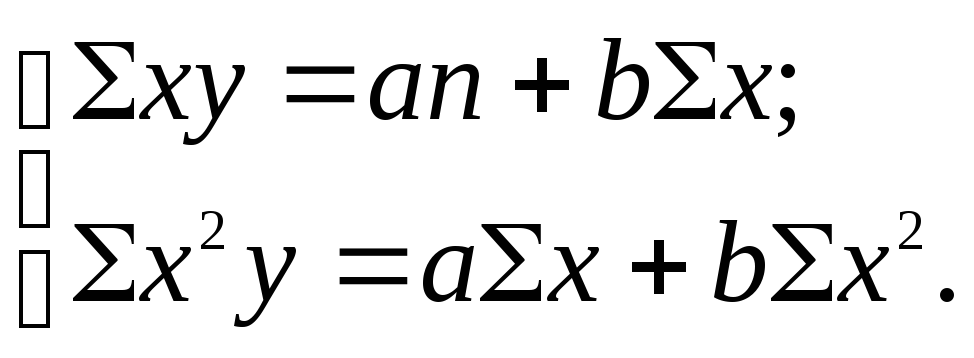(6.6)

Эта система получена в результате умножения на х и х² исходных уравнений по х и у:

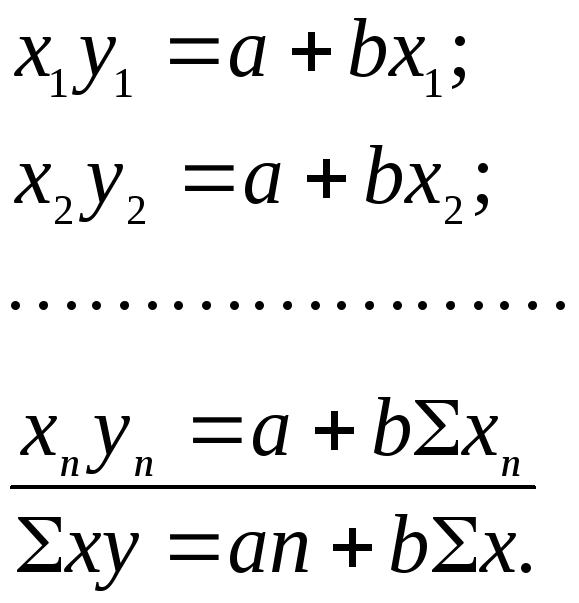
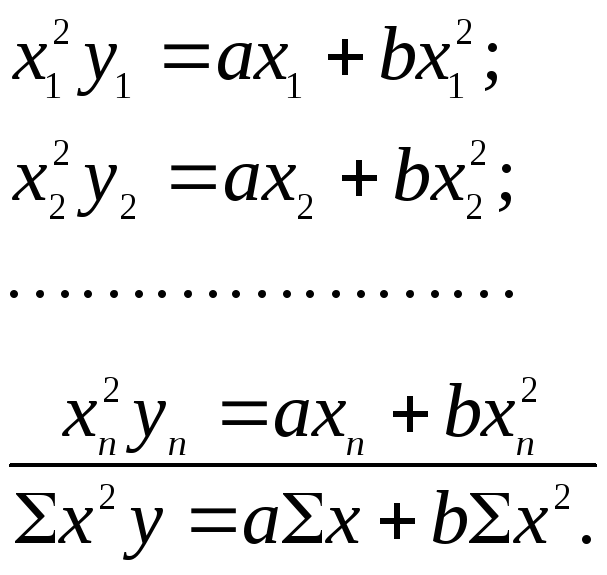
Пример.Установим зависимость между температурой воздуха в июле(х, °С) и относительной влажностью воздуха (y, %) по следующим исходным данным:

xi	14,7	14,9	15,3	15,6	16,0	16,7
yi	80	78	76	75	74	73,7

При построении графика видно, что зависимость между функцией и аргументом гиперболическая, поэтому используем общее уравнение гиперболы. Для расчета параметров а иb по способу координат точек используем данные первой и шестой пары наблюдений: х₁= 14,7,y₁= 80;x_в= 16,7,y_в= 73,7. Подставляем эти данные в общее уравнение (6.5), предварительно преобразовав его:ху = а + bх. Получим систему уравнений

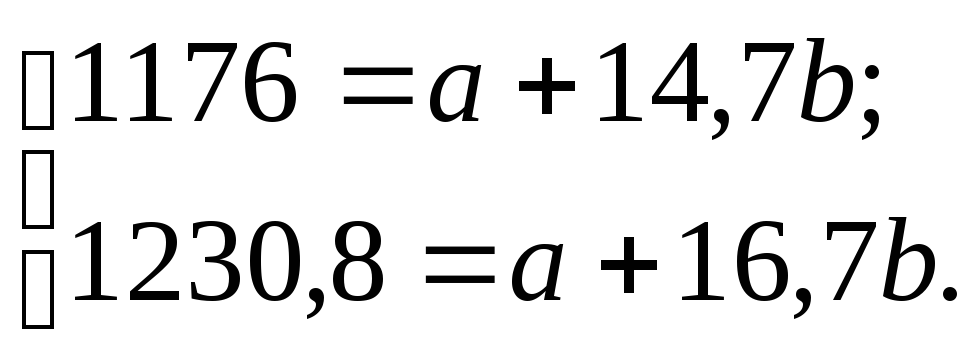
Решаем систему относительно а иb : a = 773,22;b= 27,4. В результате конкретное уравнение регрессии для гиперболической зависимости по способу координат точек будет иметь видy = 773,22/x + 27,4; η_0,99= 0,84.

Для установления параметров а и 6 по способу наименьших квадратов по уравнению (6.6) предварительно проводим соответствующие вычисления (табл. 6.3). Полученные данные подставляем в уравнение (6.6):

Делим первое уравнение на 6, второе уравнение – на 93,2 и освобождаемся от коэффициентов при неизвестном а. Затем вычитаем второе уравнение из первого и определяемb. Подставив значениеbв одно из уравнений, вычисляема. Искомое уравнение регрессии примет видy= 484597,4/x – 31280; η_0,95= 0,84.

Коэффициент точности выравнивания линии r₁ по формуле (6.4) рассчитываем таким же образом, как в п. 6.1.

Таблица 6.3

Расчет данных для уравнения линейной зависимости

x	y	xy	x2	x2y
14,7	80,0	1176,0	216,09	17287,2
14,9	78,0	1162,2	222,01	17316,78
15,3	76,0	1162,8	234,09	17790,84
15,6	75,0	1170,0	243,36	18252,00
16,0	74,0	1184,0	256,00	18994,00
16,7	73,7	1230,79	278,89	20554,19
Σ 93,2	456,7	7085,79	1450,44	110195

6.3. Параболическая зависимость

Общее уравнение параболы n-го порядка имеет вид

y = axⁿ + bx^n–1 + cx^n–2 + … + kx + l.

Если ограничиться второй ступенью независимой переменной величины х, будем иметь частный случай параболы второго порядка:

y = ax² + bx + c (6.7)

Пример. Для решения конкретной задачи используем данные примера из п. 5.2, где было рассчитано прямое корреляционное отношение (η = 0,78) и доказана его достоверность. На графике зависимость между температурой воздуха (х) и упругостью водяного пара (у) имеет вид параболы.

Для расчета коэффициентов а, b, с способом координат точек используем координаты 2-й, 4-й и 6-й точек:

x2 = 14,9;	x4 = 15,6;	x6 = 16,7;
y2 = 13,7;	y4 = 14,5;	y6 = 14,6.

Подставляя значения координат точек в общее уравнение параболы второго порядка (6.7), получаем систему уравнений, которую решаем относительно а, b, с:

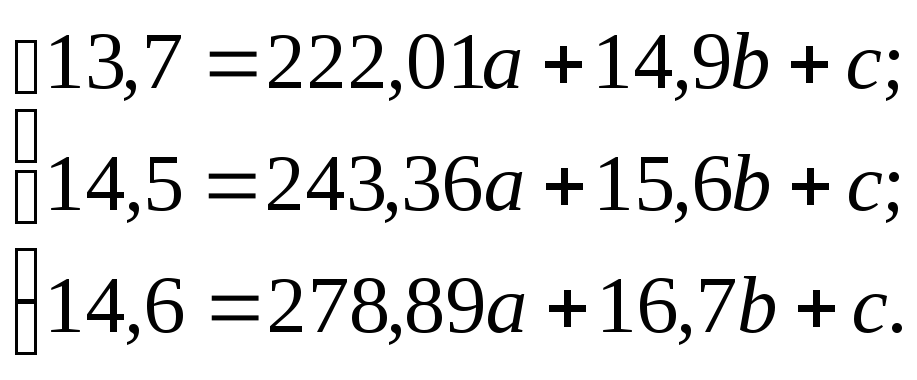
В результате a = 0,066;b = –0,19;с= 1,94. С помощью уравнения параболы (6.7) имеем следующую зависимость между переменными:y = 0,066x² – 0,19x + 1,94,η_0,95 =0,78.

Для вычисления коэффициентов а, b, с по способу наименьших квадратов используется общее уравнение параболы второго порядка. Подставив в формулу (6.7) все имеющиеся данные и просуммировав правые и левые части уравнений, получаем первое уравнение системы:

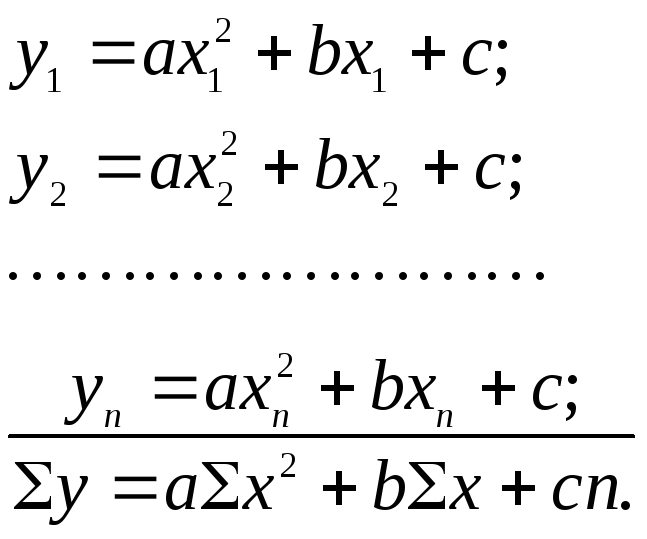
Второе и третье уравнения системы определяем путем умножения соответственно на х и х² исходного общего уравнения параболы второго порядка. В результате имеем систему трех уравнений:

(6.8)

Конкретные данные для уравнения (6.8) рассчитаны по табл. 6.4.

Пример. Решаем систему (6.8) относительно а, b, с:

84,8 = 1450,44a + 93,2b + 6c;

1319,18 = 22615,93a + 1450,44b + 93,2c;

20560,10 = 353321,18a + 22615,93b + 1450,44c;

Таблица 6.4