
- •brief contents
- •contents
- •preface
- •acknowledgments
- •about this book
- •What’s new in the second edition
- •Who should read this book
- •Roadmap
- •Advice for data miners
- •Code examples
- •Code conventions
- •Author Online
- •About the author
- •about the cover illustration
- •1 Introduction to R
- •1.2 Obtaining and installing R
- •1.3 Working with R
- •1.3.1 Getting started
- •1.3.2 Getting help
- •1.3.3 The workspace
- •1.3.4 Input and output
- •1.4 Packages
- •1.4.1 What are packages?
- •1.4.2 Installing a package
- •1.4.3 Loading a package
- •1.4.4 Learning about a package
- •1.5 Batch processing
- •1.6 Using output as input: reusing results
- •1.7 Working with large datasets
- •1.8 Working through an example
- •1.9 Summary
- •2 Creating a dataset
- •2.1 Understanding datasets
- •2.2 Data structures
- •2.2.1 Vectors
- •2.2.2 Matrices
- •2.2.3 Arrays
- •2.2.4 Data frames
- •2.2.5 Factors
- •2.2.6 Lists
- •2.3 Data input
- •2.3.1 Entering data from the keyboard
- •2.3.2 Importing data from a delimited text file
- •2.3.3 Importing data from Excel
- •2.3.4 Importing data from XML
- •2.3.5 Importing data from the web
- •2.3.6 Importing data from SPSS
- •2.3.7 Importing data from SAS
- •2.3.8 Importing data from Stata
- •2.3.9 Importing data from NetCDF
- •2.3.10 Importing data from HDF5
- •2.3.11 Accessing database management systems (DBMSs)
- •2.3.12 Importing data via Stat/Transfer
- •2.4 Annotating datasets
- •2.4.1 Variable labels
- •2.4.2 Value labels
- •2.5 Useful functions for working with data objects
- •2.6 Summary
- •3 Getting started with graphs
- •3.1 Working with graphs
- •3.2 A simple example
- •3.3 Graphical parameters
- •3.3.1 Symbols and lines
- •3.3.2 Colors
- •3.3.3 Text characteristics
- •3.3.4 Graph and margin dimensions
- •3.4 Adding text, customized axes, and legends
- •3.4.1 Titles
- •3.4.2 Axes
- •3.4.3 Reference lines
- •3.4.4 Legend
- •3.4.5 Text annotations
- •3.4.6 Math annotations
- •3.5 Combining graphs
- •3.5.1 Creating a figure arrangement with fine control
- •3.6 Summary
- •4 Basic data management
- •4.1 A working example
- •4.2 Creating new variables
- •4.3 Recoding variables
- •4.4 Renaming variables
- •4.5 Missing values
- •4.5.1 Recoding values to missing
- •4.5.2 Excluding missing values from analyses
- •4.6 Date values
- •4.6.1 Converting dates to character variables
- •4.6.2 Going further
- •4.7 Type conversions
- •4.8 Sorting data
- •4.9 Merging datasets
- •4.9.1 Adding columns to a data frame
- •4.9.2 Adding rows to a data frame
- •4.10 Subsetting datasets
- •4.10.1 Selecting (keeping) variables
- •4.10.2 Excluding (dropping) variables
- •4.10.3 Selecting observations
- •4.10.4 The subset() function
- •4.10.5 Random samples
- •4.11 Using SQL statements to manipulate data frames
- •4.12 Summary
- •5 Advanced data management
- •5.2 Numerical and character functions
- •5.2.1 Mathematical functions
- •5.2.2 Statistical functions
- •5.2.3 Probability functions
- •5.2.4 Character functions
- •5.2.5 Other useful functions
- •5.2.6 Applying functions to matrices and data frames
- •5.3 A solution for the data-management challenge
- •5.4 Control flow
- •5.4.1 Repetition and looping
- •5.4.2 Conditional execution
- •5.5 User-written functions
- •5.6 Aggregation and reshaping
- •5.6.1 Transpose
- •5.6.2 Aggregating data
- •5.6.3 The reshape2 package
- •5.7 Summary
- •6 Basic graphs
- •6.1 Bar plots
- •6.1.1 Simple bar plots
- •6.1.2 Stacked and grouped bar plots
- •6.1.3 Mean bar plots
- •6.1.4 Tweaking bar plots
- •6.1.5 Spinograms
- •6.2 Pie charts
- •6.3 Histograms
- •6.4 Kernel density plots
- •6.5 Box plots
- •6.5.1 Using parallel box plots to compare groups
- •6.5.2 Violin plots
- •6.6 Dot plots
- •6.7 Summary
- •7 Basic statistics
- •7.1 Descriptive statistics
- •7.1.1 A menagerie of methods
- •7.1.2 Even more methods
- •7.1.3 Descriptive statistics by group
- •7.1.4 Additional methods by group
- •7.1.5 Visualizing results
- •7.2 Frequency and contingency tables
- •7.2.1 Generating frequency tables
- •7.2.2 Tests of independence
- •7.2.3 Measures of association
- •7.2.4 Visualizing results
- •7.3 Correlations
- •7.3.1 Types of correlations
- •7.3.2 Testing correlations for significance
- •7.3.3 Visualizing correlations
- •7.4 T-tests
- •7.4.3 When there are more than two groups
- •7.5 Nonparametric tests of group differences
- •7.5.1 Comparing two groups
- •7.5.2 Comparing more than two groups
- •7.6 Visualizing group differences
- •7.7 Summary
- •8 Regression
- •8.1 The many faces of regression
- •8.1.1 Scenarios for using OLS regression
- •8.1.2 What you need to know
- •8.2 OLS regression
- •8.2.1 Fitting regression models with lm()
- •8.2.2 Simple linear regression
- •8.2.3 Polynomial regression
- •8.2.4 Multiple linear regression
- •8.2.5 Multiple linear regression with interactions
- •8.3 Regression diagnostics
- •8.3.1 A typical approach
- •8.3.2 An enhanced approach
- •8.3.3 Global validation of linear model assumption
- •8.3.4 Multicollinearity
- •8.4 Unusual observations
- •8.4.1 Outliers
- •8.4.3 Influential observations
- •8.5 Corrective measures
- •8.5.1 Deleting observations
- •8.5.2 Transforming variables
- •8.5.3 Adding or deleting variables
- •8.5.4 Trying a different approach
- •8.6 Selecting the “best” regression model
- •8.6.1 Comparing models
- •8.6.2 Variable selection
- •8.7 Taking the analysis further
- •8.7.1 Cross-validation
- •8.7.2 Relative importance
- •8.8 Summary
- •9 Analysis of variance
- •9.1 A crash course on terminology
- •9.2 Fitting ANOVA models
- •9.2.1 The aov() function
- •9.2.2 The order of formula terms
- •9.3.1 Multiple comparisons
- •9.3.2 Assessing test assumptions
- •9.4 One-way ANCOVA
- •9.4.1 Assessing test assumptions
- •9.4.2 Visualizing the results
- •9.6 Repeated measures ANOVA
- •9.7 Multivariate analysis of variance (MANOVA)
- •9.7.1 Assessing test assumptions
- •9.7.2 Robust MANOVA
- •9.8 ANOVA as regression
- •9.9 Summary
- •10 Power analysis
- •10.1 A quick review of hypothesis testing
- •10.2 Implementing power analysis with the pwr package
- •10.2.1 t-tests
- •10.2.2 ANOVA
- •10.2.3 Correlations
- •10.2.4 Linear models
- •10.2.5 Tests of proportions
- •10.2.7 Choosing an appropriate effect size in novel situations
- •10.3 Creating power analysis plots
- •10.4 Other packages
- •10.5 Summary
- •11 Intermediate graphs
- •11.1 Scatter plots
- •11.1.3 3D scatter plots
- •11.1.4 Spinning 3D scatter plots
- •11.1.5 Bubble plots
- •11.2 Line charts
- •11.3 Corrgrams
- •11.4 Mosaic plots
- •11.5 Summary
- •12 Resampling statistics and bootstrapping
- •12.1 Permutation tests
- •12.2 Permutation tests with the coin package
- •12.2.2 Independence in contingency tables
- •12.2.3 Independence between numeric variables
- •12.2.5 Going further
- •12.3 Permutation tests with the lmPerm package
- •12.3.1 Simple and polynomial regression
- •12.3.2 Multiple regression
- •12.4 Additional comments on permutation tests
- •12.5 Bootstrapping
- •12.6 Bootstrapping with the boot package
- •12.6.1 Bootstrapping a single statistic
- •12.6.2 Bootstrapping several statistics
- •12.7 Summary
- •13 Generalized linear models
- •13.1 Generalized linear models and the glm() function
- •13.1.1 The glm() function
- •13.1.2 Supporting functions
- •13.1.3 Model fit and regression diagnostics
- •13.2 Logistic regression
- •13.2.1 Interpreting the model parameters
- •13.2.2 Assessing the impact of predictors on the probability of an outcome
- •13.2.3 Overdispersion
- •13.2.4 Extensions
- •13.3 Poisson regression
- •13.3.1 Interpreting the model parameters
- •13.3.2 Overdispersion
- •13.3.3 Extensions
- •13.4 Summary
- •14 Principal components and factor analysis
- •14.1 Principal components and factor analysis in R
- •14.2 Principal components
- •14.2.1 Selecting the number of components to extract
- •14.2.2 Extracting principal components
- •14.2.3 Rotating principal components
- •14.2.4 Obtaining principal components scores
- •14.3 Exploratory factor analysis
- •14.3.1 Deciding how many common factors to extract
- •14.3.2 Extracting common factors
- •14.3.3 Rotating factors
- •14.3.4 Factor scores
- •14.4 Other latent variable models
- •14.5 Summary
- •15 Time series
- •15.1 Creating a time-series object in R
- •15.2 Smoothing and seasonal decomposition
- •15.2.1 Smoothing with simple moving averages
- •15.2.2 Seasonal decomposition
- •15.3 Exponential forecasting models
- •15.3.1 Simple exponential smoothing
- •15.3.3 The ets() function and automated forecasting
- •15.4 ARIMA forecasting models
- •15.4.1 Prerequisite concepts
- •15.4.2 ARMA and ARIMA models
- •15.4.3 Automated ARIMA forecasting
- •15.5 Going further
- •15.6 Summary
- •16 Cluster analysis
- •16.1 Common steps in cluster analysis
- •16.2 Calculating distances
- •16.3 Hierarchical cluster analysis
- •16.4 Partitioning cluster analysis
- •16.4.2 Partitioning around medoids
- •16.5 Avoiding nonexistent clusters
- •16.6 Summary
- •17 Classification
- •17.1 Preparing the data
- •17.2 Logistic regression
- •17.3 Decision trees
- •17.3.1 Classical decision trees
- •17.3.2 Conditional inference trees
- •17.4 Random forests
- •17.5 Support vector machines
- •17.5.1 Tuning an SVM
- •17.6 Choosing a best predictive solution
- •17.7 Using the rattle package for data mining
- •17.8 Summary
- •18 Advanced methods for missing data
- •18.1 Steps in dealing with missing data
- •18.2 Identifying missing values
- •18.3 Exploring missing-values patterns
- •18.3.1 Tabulating missing values
- •18.3.2 Exploring missing data visually
- •18.3.3 Using correlations to explore missing values
- •18.4 Understanding the sources and impact of missing data
- •18.5 Rational approaches for dealing with incomplete data
- •18.6 Complete-case analysis (listwise deletion)
- •18.7 Multiple imputation
- •18.8 Other approaches to missing data
- •18.8.1 Pairwise deletion
- •18.8.2 Simple (nonstochastic) imputation
- •18.9 Summary
- •19 Advanced graphics with ggplot2
- •19.1 The four graphics systems in R
- •19.2 An introduction to the ggplot2 package
- •19.3 Specifying the plot type with geoms
- •19.4 Grouping
- •19.5 Faceting
- •19.6 Adding smoothed lines
- •19.7 Modifying the appearance of ggplot2 graphs
- •19.7.1 Axes
- •19.7.2 Legends
- •19.7.3 Scales
- •19.7.4 Themes
- •19.7.5 Multiple graphs per page
- •19.8 Saving graphs
- •19.9 Summary
- •20 Advanced programming
- •20.1 A review of the language
- •20.1.1 Data types
- •20.1.2 Control structures
- •20.1.3 Creating functions
- •20.2 Working with environments
- •20.3 Object-oriented programming
- •20.3.1 Generic functions
- •20.3.2 Limitations of the S3 model
- •20.4 Writing efficient code
- •20.5 Debugging
- •20.5.1 Common sources of errors
- •20.5.2 Debugging tools
- •20.5.3 Session options that support debugging
- •20.6 Going further
- •20.7 Summary
- •21 Creating a package
- •21.1 Nonparametric analysis and the npar package
- •21.1.1 Comparing groups with the npar package
- •21.2 Developing the package
- •21.2.1 Computing the statistics
- •21.2.2 Printing the results
- •21.2.3 Summarizing the results
- •21.2.4 Plotting the results
- •21.2.5 Adding sample data to the package
- •21.3 Creating the package documentation
- •21.4 Building the package
- •21.5 Going further
- •21.6 Summary
- •22 Creating dynamic reports
- •22.1 A template approach to reports
- •22.2 Creating dynamic reports with R and Markdown
- •22.3 Creating dynamic reports with R and LaTeX
- •22.4 Creating dynamic reports with R and Open Document
- •22.5 Creating dynamic reports with R and Microsoft Word
- •22.6 Summary
- •afterword Into the rabbit hole
- •appendix A Graphical user interfaces
- •appendix B Customizing the startup environment
- •appendix C Exporting data from R
- •Delimited text file
- •Excel spreadsheet
- •Statistical applications
- •appendix D Matrix algebra in R
- •appendix E Packages used in this book
- •appendix F Working with large datasets
- •F.1 Efficient programming
- •F.2 Storing data outside of RAM
- •F.3 Analytic packages for out-of-memory data
- •F.4 Comprehensive solutions for working with enormous datasets
- •appendix G Updating an R installation
- •G.1 Automated installation (Windows only)
- •G.2 Manual installation (Windows and Mac OS X)
- •G.3 Updating an R installation (Linux)
- •references
- •index
- •Symbols
- •Numerics
- •23.1 The lattice package
- •23.2 Conditioning variables
- •23.3 Panel functions
- •23.4 Grouping variables
- •23.5 Graphic parameters
- •23.6 Customizing plot strips
- •23.7 Page arrangement
- •23.8 Going further

One-way ANCOVA |
223 |
Bartlett’s test indicates that the variances in the five groups don’t differ significantly (p = 0.97). Other possible tests include the Fligner–Killeen test (provided by the fligner.test() function) and the Brown–Forsythe test (provided by the hov() function in the HH package). Although not shown, the other two tests reach the same conclusion.
Finally, analysis of variance methodologies can be sensitive to the presence of outliers. You can test for outliers using the outlierTest() function in the car package:
>library(car)
>outlierTest(fit)
No |
Studentized residuals with Bonferonni p < 0.05 |
||
Largest |rstudent|: |
|
||
|
rstudent |
unadjusted p-value Bonferonni p |
|
19 |
2.251149 |
0.029422 |
NA |
From the output, you can see that there’s no indication of outliers in the cholesterol data (NA occurs when p > 1). Taking the Q-Q plot, Bartlett’s test, and outlier test together, the data appear to fit the ANOVA model quite well. This, in turn, adds to your confidence in the results.
9.4One-way ANCOVA
A one-way analysis of covariance (ANCOVA) extends the one-way ANOVA to include one or more quantitative covariates. This example comes from the litter dataset in the multcomp package (see Westfall et al., 1999). Pregnant mice were divided into four treatment groups; each group received a different dose of a drug (0, 5, 50, or 500). The mean post-birth weight for each litter was the dependent variable, and gestation time was included as a covariate. The analysis is given in the following listing.
Listing 9.3 One-way ANCOVA
>data(litter, package="multcomp")
>attach(litter)
>table(dose)
dose |
|
|
|
0 |
5 |
50 |
500 |
20 |
19 |
18 |
17 |
> aggregate(weight, by=list(dose), FUN=mean) Group.1 x
10 32.3
25 29.3
350 29.9
4500 29.6
>fit <- aov(weight ~ gesttime + dose)
>summary(fit)
|
Df |
Sum Sq Mean Sq F value |
Pr(>F) |
|
||
gesttime |
1 |
134.30 |
134.30 |
8.0493 |
0.005971 |
** |
dose |
3 |
137.12 |
45.71 |
2.7394 |
0.049883 |
* |
Residuals |
69 1151.27 |
16.69 |
|
|
|
|
--- |
|
|
|
|
|
|
Signif. codes: |
0 '***' |
0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 |
||||

224 |
CHAPTER 9 Analysis of variance |
From the table() function, you can see that there is an unequal number of litters at each dosage level, with 20 litters at zero dosage (no drug) and 17 litters at dosage 500. Based on the group means provided by the aggregate() function, the no-drug group had the highest mean litter weight (32.3). The ANCOVA F tests indicate that (a) gestation time was related to birth weight, and (b) drug dosage was related to birth weight after controlling for gestation time. The mean birth weight isn’t the same for each of the drug dosages, after controlling for gestation time.
Because you’re using a covariate, you may want to obtain adjusted group means— that is, the group means obtained after partialing out the effects of the covariate. You can use the effect() function in the effects library to calculate adjusted means:
>library(effects)
>effect("dose", fit)
dose effect dose
0 5 50 500
32.4 28.9 30.6 29.3
In this case, the adjusted means are similar to the unadjusted means produced by the aggregate() function, but this won’t always be the case. The effects package provides a powerful method of obtaining adjusted means for complex research designs and presenting them visually. See the package documentation on CRAN for more details.
As with the one-way ANOVA example in the last section, the F test for dose indicates that the treatments don’t have the same mean birth weight, but it doesn’t tell you which means differ from one another. Again you can use the multiple comparison procedures provided by the multcomp package to compute all pairwise mean comparisons. Additionally, the multcomp package can be used to test specific user-defined hypotheses about the means.
Suppose you’re interested in whether the no-drug condition differs from the threedrug condition. The code in the following listing can be used to test this hypothesis.
Listing 9.4 Multiple comparisons employing user-supplied contrasts
>library(multcomp)
>contrast <- rbind("no drug vs. drug" = c(3, -1, -1, -1))
>summary(glht(fit, linfct=mcp(dose=contrast)))
Multiple Comparisons of Means: User-defined Contrasts
Fit: aov(formula = weight ~ gesttime + dose)
Linear Hypotheses: |
|
|
|
|
|
|
|
Estimate Std. Error |
t |
value Pr(>|t|) |
|
||
no drug vs. drug == 0 |
8.284 |
3.209 |
|
2.581 |
0.0120 |
* |
--- |
|
|
|
|
|
|
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' |
0.05 '.' 0.1 ' ' 1 |
|||||

One-way ANCOVA |
225 |
The contrast c(3, -1, -1, -1) specifies a comparison of the first group with the average of the other three. The hypothesis is tested with a t statistic (2.581 in this case), which is significant at the p < .05 level. Therefore, you can conclude that the no-drug group has a higher birth weight than drug conditions. Other contrasts can be added to the rbind() function (see help(glht) for details).
9.4.1Assessing test assumptions
ANCOVA designs make the same normality and homogeneity of variance assumptions described for ANOVA designs, and you can test these assumptions using the same procedures described in section 9.3.2. In addition, standard ANCOVA designs assume homogeneity of regression slopes. In this case, it’s assumed that the regression slope for predicting birth weight from gestation time is the same in each of the four treatment groups. A test for the homogeneity of regression slopes can be obtained by including a gestation × dose interaction term in your ANCOVA model. A significant interaction would imply that the relationship between gestation and birth weight depends on the level of the dose variable. The code and results are provided in the following listing.
Listing 9.5 Testing for homogeneity of regression slopes
>library(multcomp)
>fit2 <- aov(weight ~ gesttime*dose, data=litter)
>summary(fit2)
|
Df Sum Sq |
Mean Sq F value |
Pr(>F) |
|
|
||
gesttime |
1 |
134 |
134 |
8.29 |
0.0054 |
** |
|
dose |
3 |
137 |
46 |
2.82 |
0.0456 |
* |
|
gesttime:dose |
3 |
82 |
27 |
1.68 |
0.1789 |
|
|
Residuals |
66 |
1069 |
16 |
|
|
|
|
--- |
|
|
|
|
|
|
|
Signif. codes: |
|
0 '***' |
0.001 '**' 0.01 |
'*' 0.05 |
'.' 0.1 ' ' 1 |
||
The interaction is nonsignificant, supporting the assumption of equality of slopes. If the assumption is untenable, you could try transforming the covariate or dependent variable, using a model that accounts for separate slopes, or employing a nonparametric ANCOVA method that doesn’t require homogeneity of regression slopes. See the sm.ancova() function in the sm package for an example of the latter.
9.4.2Visualizing the results
The ancova() function in the HH package provides a plot of the relationship between the dependent variable, the covariate, and the factor. For example,
>library(HH)
>ancova(weight ~ gesttime + dose, data=litter)
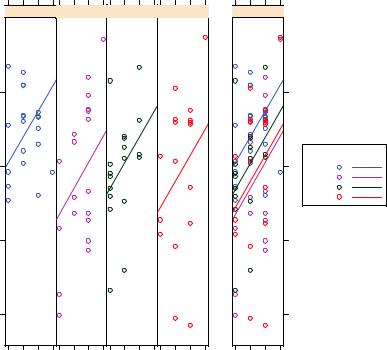
produces the plot shown in figure 9.5. (The figure has been modified to display better in black and white and will look slightly different when you run the code yourself.)
226 |
CHAPTER 9 Analysis of variance |
|
|
weight ~ gesttime + dose |
|
|||
|
21.5 |
22.5 |
21.5 |
22.5 |
|
|
|
0 |
5 |
50 |
500 |
superpose |
|
35 |
|
|
|
|
|
|
30 |
|
|
|
|
|
|
weight |
|
|
|
|
|
|
25 |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
21.5 |
22.5 |
21.5 |
22.5 |
|
21.5 |
22.5 |
|
|
|
gesttime |
|
|
|
dose
0
5
50
500
Figure 9.5 Plot of the relationship between gestation time and birth weight for each of four drug treatment groups
Here you can see that the regression lines for predicting birth weight from gestation time are parallel in each group but have different intercepts. As gestation time increases, birth weight increases. Additionally, you can see that the zero-dose group has the largest intercept and the five-dose group has the lowest intercept. The lines are parallel because they’ve been specified to be. If you used the statement ancova(weight ~ gesttime*dose) instead, you’d generate a plot that allows both the slopes and intercepts to vary by group. This approach is useful for visualizing the case where the homogeneity of regression slopes doesn’t hold.
9.5Two-way factorial ANOVA
In a two-way factorial ANOVA, subjects are assigned to groups that are formed from the cross-classification of two factors. This example uses the ToothGrowth dataset in the base installation to demonstrate a two-way between-groups ANOVA. Sixty guinea pigs are randomly assigned to receive one of three levels of ascorbic acid (0.5, 1, or 2 mg) and one of two delivery methods (orange juice or Vitamin C), under the restriction that each treatment combination has 10 guinea pigs. The dependent variable is tooth length. The following listing shows the code for the analysis.

Two-way factorial ANOVA |
227 |
Listing 9.6 Two-way ANOVA
>attach(ToothGrowth)
>table(supp, dose)
dose
supp 0.5 1 2 OJ 10 10 10 VC 10 10 10
> aggregate(len, by=list(supp, dose), FUN=mean)
|
Group.1 Group.2 |
x |
|
1 |
OJ |
0.5 |
13.23 |
2 |
VC |
0.5 |
7.98 |
3 |
OJ |
1.0 |
22.70 |
4 |
VC |
1.0 |
16.77 |
5 |
OJ |
2.0 |
26.06 |
6 |
VC |
2.0 |
26.14 |
> aggregate(len, by=list(supp, dose), FUN=sd)
|
Group.1 Group.2 |
x |
|
1 |
OJ |
0.5 |
4.46 |
2 |
VC |
0.5 |
2.75 |
3 |
OJ |
1.0 |
3.91 |
4 |
VC |
1.0 |
2.52 |
5 |
OJ |
2.0 |
2.66 |
6 |
VC |
2.0 |
4.80 |
>dose <- factor(dose)
>fit <- aov(len ~ supp*dose)
>summary(fit)
|
Df Sum Sq Mean Sq |
F value |
|
Pr(>F) |
|
||
supp |
1 |
205 |
205 |
15.57 |
0.00023 |
*** |
|
dose |
2 |
2426 |
1213 |
92.00 |
< |
2e-16 |
*** |
supp:dose |
2 |
108 |
54 |
4.11 |
0.02186 |
* |
|
Residuals |
54 |
712 |
13 |
|
|
|
|
--- |
|
|
|
|
|
|
|
Signif. codes: |
0 ‘***’ 0.001 |
‘**’ 0.01 |
‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 |
||||
> detach(ToothGrowth)
The table statement indicates that you have a balanced design (equal sample sizes in each cell of the design), and the aggregate statements provide the cell means and standard deviations. The dose variable is converted to a factor so that the aov() function will treat it as a grouping variable, rather than a numeric covariate. The ANOVA table provided by the summary() function indicates that both main effects (supp and dose) and the interaction between these factors are significant.
You can visualize the results in several ways. You can use the interaction.plot() function to display the interaction in a two-way ANOVA. The code is
interaction.plot(dose, supp, len, type="b", col=c("red","blue"), pch=c(16, 18),
main = "Interaction between Dose and Supplement Type")

228 |
CHAPTER 9 Analysis of variance |
and the resulting plot is presented in figure 9.6. The plot provides the mean tooth length for each supplement at each dosage.
Figure 9.6 Interaction between dose and delivery mechanism on tooth growth. The plot of means was created using the interaction.plot() function.
Interaction between Dose and Supplement Type
|
25 |
|
supp |
|
|
|
|
|
|
|
VC |
|
|
|
OJ |
len |
20 |
|
|
|
|
|
|
mean of |
15 |
|
|
|
10 |
|
|
|
0.5 |
1 |
2 |
|
|
|
dose |
With a little finesse, you can get an interaction plot out of the plotmeans() function in the gplots package. The following code produces the graph in figure 9.7:
library(gplots)
plotmeans(len ~ interaction(supp, dose, sep=" "), connect=list(c(1,3,5),c(2,4,6)), col=c("red", "darkgreen"),
main = "Interaction Plot with 95% CIs", xlab="Treatment and Dose Combination")
The graph includes the means, as well as error bars (95% confidence intervals) and sample sizes.
Figure 9.7 Interaction between dose and delivery mechanism on tooth growth. The mean plot with 95% confidence intervals was created by the plotmeans() function.
Interaction Plot with 95% CIs
30 |
|
|
|
|
|
25 |
|
|
|
|
|
20 |
|
|
|
|
|
len |
|
|
|
|
|
15 |
|
|
|
|
|
10 |
|
|
|
|
|
n=10 |
n=10 |
n=10 |
n=10 |
n=10 |
n=10 |
OJ 0.5 |
VC 0.5 |
OJ 1 |
VC 1 |
OJ 2 |
VC 2 |
Treatment and Dose Combination
