
- •brief contents
- •contents
- •preface
- •acknowledgments
- •about this book
- •What’s new in the second edition
- •Who should read this book
- •Roadmap
- •Advice for data miners
- •Code examples
- •Code conventions
- •Author Online
- •About the author
- •about the cover illustration
- •1 Introduction to R
- •1.2 Obtaining and installing R
- •1.3 Working with R
- •1.3.1 Getting started
- •1.3.2 Getting help
- •1.3.3 The workspace
- •1.3.4 Input and output
- •1.4 Packages
- •1.4.1 What are packages?
- •1.4.2 Installing a package
- •1.4.3 Loading a package
- •1.4.4 Learning about a package
- •1.5 Batch processing
- •1.6 Using output as input: reusing results
- •1.7 Working with large datasets
- •1.8 Working through an example
- •1.9 Summary
- •2 Creating a dataset
- •2.1 Understanding datasets
- •2.2 Data structures
- •2.2.1 Vectors
- •2.2.2 Matrices
- •2.2.3 Arrays
- •2.2.4 Data frames
- •2.2.5 Factors
- •2.2.6 Lists
- •2.3 Data input
- •2.3.1 Entering data from the keyboard
- •2.3.2 Importing data from a delimited text file
- •2.3.3 Importing data from Excel
- •2.3.4 Importing data from XML
- •2.3.5 Importing data from the web
- •2.3.6 Importing data from SPSS
- •2.3.7 Importing data from SAS
- •2.3.8 Importing data from Stata
- •2.3.9 Importing data from NetCDF
- •2.3.10 Importing data from HDF5
- •2.3.11 Accessing database management systems (DBMSs)
- •2.3.12 Importing data via Stat/Transfer
- •2.4 Annotating datasets
- •2.4.1 Variable labels
- •2.4.2 Value labels
- •2.5 Useful functions for working with data objects
- •2.6 Summary
- •3 Getting started with graphs
- •3.1 Working with graphs
- •3.2 A simple example
- •3.3 Graphical parameters
- •3.3.1 Symbols and lines
- •3.3.2 Colors
- •3.3.3 Text characteristics
- •3.3.4 Graph and margin dimensions
- •3.4 Adding text, customized axes, and legends
- •3.4.1 Titles
- •3.4.2 Axes
- •3.4.3 Reference lines
- •3.4.4 Legend
- •3.4.5 Text annotations
- •3.4.6 Math annotations
- •3.5 Combining graphs
- •3.5.1 Creating a figure arrangement with fine control
- •3.6 Summary
- •4 Basic data management
- •4.1 A working example
- •4.2 Creating new variables
- •4.3 Recoding variables
- •4.4 Renaming variables
- •4.5 Missing values
- •4.5.1 Recoding values to missing
- •4.5.2 Excluding missing values from analyses
- •4.6 Date values
- •4.6.1 Converting dates to character variables
- •4.6.2 Going further
- •4.7 Type conversions
- •4.8 Sorting data
- •4.9 Merging datasets
- •4.9.1 Adding columns to a data frame
- •4.9.2 Adding rows to a data frame
- •4.10 Subsetting datasets
- •4.10.1 Selecting (keeping) variables
- •4.10.2 Excluding (dropping) variables
- •4.10.3 Selecting observations
- •4.10.4 The subset() function
- •4.10.5 Random samples
- •4.11 Using SQL statements to manipulate data frames
- •4.12 Summary
- •5 Advanced data management
- •5.2 Numerical and character functions
- •5.2.1 Mathematical functions
- •5.2.2 Statistical functions
- •5.2.3 Probability functions
- •5.2.4 Character functions
- •5.2.5 Other useful functions
- •5.2.6 Applying functions to matrices and data frames
- •5.3 A solution for the data-management challenge
- •5.4 Control flow
- •5.4.1 Repetition and looping
- •5.4.2 Conditional execution
- •5.5 User-written functions
- •5.6 Aggregation and reshaping
- •5.6.1 Transpose
- •5.6.2 Aggregating data
- •5.6.3 The reshape2 package
- •5.7 Summary
- •6 Basic graphs
- •6.1 Bar plots
- •6.1.1 Simple bar plots
- •6.1.2 Stacked and grouped bar plots
- •6.1.3 Mean bar plots
- •6.1.4 Tweaking bar plots
- •6.1.5 Spinograms
- •6.2 Pie charts
- •6.3 Histograms
- •6.4 Kernel density plots
- •6.5 Box plots
- •6.5.1 Using parallel box plots to compare groups
- •6.5.2 Violin plots
- •6.6 Dot plots
- •6.7 Summary
- •7 Basic statistics
- •7.1 Descriptive statistics
- •7.1.1 A menagerie of methods
- •7.1.2 Even more methods
- •7.1.3 Descriptive statistics by group
- •7.1.4 Additional methods by group
- •7.1.5 Visualizing results
- •7.2 Frequency and contingency tables
- •7.2.1 Generating frequency tables
- •7.2.2 Tests of independence
- •7.2.3 Measures of association
- •7.2.4 Visualizing results
- •7.3 Correlations
- •7.3.1 Types of correlations
- •7.3.2 Testing correlations for significance
- •7.3.3 Visualizing correlations
- •7.4 T-tests
- •7.4.3 When there are more than two groups
- •7.5 Nonparametric tests of group differences
- •7.5.1 Comparing two groups
- •7.5.2 Comparing more than two groups
- •7.6 Visualizing group differences
- •7.7 Summary
- •8 Regression
- •8.1 The many faces of regression
- •8.1.1 Scenarios for using OLS regression
- •8.1.2 What you need to know
- •8.2 OLS regression
- •8.2.1 Fitting regression models with lm()
- •8.2.2 Simple linear regression
- •8.2.3 Polynomial regression
- •8.2.4 Multiple linear regression
- •8.2.5 Multiple linear regression with interactions
- •8.3 Regression diagnostics
- •8.3.1 A typical approach
- •8.3.2 An enhanced approach
- •8.3.3 Global validation of linear model assumption
- •8.3.4 Multicollinearity
- •8.4 Unusual observations
- •8.4.1 Outliers
- •8.4.3 Influential observations
- •8.5 Corrective measures
- •8.5.1 Deleting observations
- •8.5.2 Transforming variables
- •8.5.3 Adding or deleting variables
- •8.5.4 Trying a different approach
- •8.6 Selecting the “best” regression model
- •8.6.1 Comparing models
- •8.6.2 Variable selection
- •8.7 Taking the analysis further
- •8.7.1 Cross-validation
- •8.7.2 Relative importance
- •8.8 Summary
- •9 Analysis of variance
- •9.1 A crash course on terminology
- •9.2 Fitting ANOVA models
- •9.2.1 The aov() function
- •9.2.2 The order of formula terms
- •9.3.1 Multiple comparisons
- •9.3.2 Assessing test assumptions
- •9.4 One-way ANCOVA
- •9.4.1 Assessing test assumptions
- •9.4.2 Visualizing the results
- •9.6 Repeated measures ANOVA
- •9.7 Multivariate analysis of variance (MANOVA)
- •9.7.1 Assessing test assumptions
- •9.7.2 Robust MANOVA
- •9.8 ANOVA as regression
- •9.9 Summary
- •10 Power analysis
- •10.1 A quick review of hypothesis testing
- •10.2 Implementing power analysis with the pwr package
- •10.2.1 t-tests
- •10.2.2 ANOVA
- •10.2.3 Correlations
- •10.2.4 Linear models
- •10.2.5 Tests of proportions
- •10.2.7 Choosing an appropriate effect size in novel situations
- •10.3 Creating power analysis plots
- •10.4 Other packages
- •10.5 Summary
- •11 Intermediate graphs
- •11.1 Scatter plots
- •11.1.3 3D scatter plots
- •11.1.4 Spinning 3D scatter plots
- •11.1.5 Bubble plots
- •11.2 Line charts
- •11.3 Corrgrams
- •11.4 Mosaic plots
- •11.5 Summary
- •12 Resampling statistics and bootstrapping
- •12.1 Permutation tests
- •12.2 Permutation tests with the coin package
- •12.2.2 Independence in contingency tables
- •12.2.3 Independence between numeric variables
- •12.2.5 Going further
- •12.3 Permutation tests with the lmPerm package
- •12.3.1 Simple and polynomial regression
- •12.3.2 Multiple regression
- •12.4 Additional comments on permutation tests
- •12.5 Bootstrapping
- •12.6 Bootstrapping with the boot package
- •12.6.1 Bootstrapping a single statistic
- •12.6.2 Bootstrapping several statistics
- •12.7 Summary
- •13 Generalized linear models
- •13.1 Generalized linear models and the glm() function
- •13.1.1 The glm() function
- •13.1.2 Supporting functions
- •13.1.3 Model fit and regression diagnostics
- •13.2 Logistic regression
- •13.2.1 Interpreting the model parameters
- •13.2.2 Assessing the impact of predictors on the probability of an outcome
- •13.2.3 Overdispersion
- •13.2.4 Extensions
- •13.3 Poisson regression
- •13.3.1 Interpreting the model parameters
- •13.3.2 Overdispersion
- •13.3.3 Extensions
- •13.4 Summary
- •14 Principal components and factor analysis
- •14.1 Principal components and factor analysis in R
- •14.2 Principal components
- •14.2.1 Selecting the number of components to extract
- •14.2.2 Extracting principal components
- •14.2.3 Rotating principal components
- •14.2.4 Obtaining principal components scores
- •14.3 Exploratory factor analysis
- •14.3.1 Deciding how many common factors to extract
- •14.3.2 Extracting common factors
- •14.3.3 Rotating factors
- •14.3.4 Factor scores
- •14.4 Other latent variable models
- •14.5 Summary
- •15 Time series
- •15.1 Creating a time-series object in R
- •15.2 Smoothing and seasonal decomposition
- •15.2.1 Smoothing with simple moving averages
- •15.2.2 Seasonal decomposition
- •15.3 Exponential forecasting models
- •15.3.1 Simple exponential smoothing
- •15.3.3 The ets() function and automated forecasting
- •15.4 ARIMA forecasting models
- •15.4.1 Prerequisite concepts
- •15.4.2 ARMA and ARIMA models
- •15.4.3 Automated ARIMA forecasting
- •15.5 Going further
- •15.6 Summary
- •16 Cluster analysis
- •16.1 Common steps in cluster analysis
- •16.2 Calculating distances
- •16.3 Hierarchical cluster analysis
- •16.4 Partitioning cluster analysis
- •16.4.2 Partitioning around medoids
- •16.5 Avoiding nonexistent clusters
- •16.6 Summary
- •17 Classification
- •17.1 Preparing the data
- •17.2 Logistic regression
- •17.3 Decision trees
- •17.3.1 Classical decision trees
- •17.3.2 Conditional inference trees
- •17.4 Random forests
- •17.5 Support vector machines
- •17.5.1 Tuning an SVM
- •17.6 Choosing a best predictive solution
- •17.7 Using the rattle package for data mining
- •17.8 Summary
- •18 Advanced methods for missing data
- •18.1 Steps in dealing with missing data
- •18.2 Identifying missing values
- •18.3 Exploring missing-values patterns
- •18.3.1 Tabulating missing values
- •18.3.2 Exploring missing data visually
- •18.3.3 Using correlations to explore missing values
- •18.4 Understanding the sources and impact of missing data
- •18.5 Rational approaches for dealing with incomplete data
- •18.6 Complete-case analysis (listwise deletion)
- •18.7 Multiple imputation
- •18.8 Other approaches to missing data
- •18.8.1 Pairwise deletion
- •18.8.2 Simple (nonstochastic) imputation
- •18.9 Summary
- •19 Advanced graphics with ggplot2
- •19.1 The four graphics systems in R
- •19.2 An introduction to the ggplot2 package
- •19.3 Specifying the plot type with geoms
- •19.4 Grouping
- •19.5 Faceting
- •19.6 Adding smoothed lines
- •19.7 Modifying the appearance of ggplot2 graphs
- •19.7.1 Axes
- •19.7.2 Legends
- •19.7.3 Scales
- •19.7.4 Themes
- •19.7.5 Multiple graphs per page
- •19.8 Saving graphs
- •19.9 Summary
- •20 Advanced programming
- •20.1 A review of the language
- •20.1.1 Data types
- •20.1.2 Control structures
- •20.1.3 Creating functions
- •20.2 Working with environments
- •20.3 Object-oriented programming
- •20.3.1 Generic functions
- •20.3.2 Limitations of the S3 model
- •20.4 Writing efficient code
- •20.5 Debugging
- •20.5.1 Common sources of errors
- •20.5.2 Debugging tools
- •20.5.3 Session options that support debugging
- •20.6 Going further
- •20.7 Summary
- •21 Creating a package
- •21.1 Nonparametric analysis and the npar package
- •21.1.1 Comparing groups with the npar package
- •21.2 Developing the package
- •21.2.1 Computing the statistics
- •21.2.2 Printing the results
- •21.2.3 Summarizing the results
- •21.2.4 Plotting the results
- •21.2.5 Adding sample data to the package
- •21.3 Creating the package documentation
- •21.4 Building the package
- •21.5 Going further
- •21.6 Summary
- •22 Creating dynamic reports
- •22.1 A template approach to reports
- •22.2 Creating dynamic reports with R and Markdown
- •22.3 Creating dynamic reports with R and LaTeX
- •22.4 Creating dynamic reports with R and Open Document
- •22.5 Creating dynamic reports with R and Microsoft Word
- •22.6 Summary
- •afterword Into the rabbit hole
- •appendix A Graphical user interfaces
- •appendix B Customizing the startup environment
- •appendix C Exporting data from R
- •Delimited text file
- •Excel spreadsheet
- •Statistical applications
- •appendix D Matrix algebra in R
- •appendix E Packages used in this book
- •appendix F Working with large datasets
- •F.1 Efficient programming
- •F.2 Storing data outside of RAM
- •F.3 Analytic packages for out-of-memory data
- •F.4 Comprehensive solutions for working with enormous datasets
- •appendix G Updating an R installation
- •G.1 Automated installation (Windows only)
- •G.2 Manual installation (Windows and Mac OS X)
- •G.3 Updating an R installation (Linux)
- •references
- •index
- •Symbols
- •Numerics
- •23.1 The lattice package
- •23.2 Conditioning variables
- •23.3 Panel functions
- •23.4 Grouping variables
- •23.5 Graphic parameters
- •23.6 Customizing plot strips
- •23.7 Page arrangement
- •23.8 Going further
Advanced graphics with ggplot2
This chapter covers
■An introduction to the ggplot2 package
■Using shape, color, and size to visualize multivariate data
■Comparing groups with faceted graphs
■Customizing ggplot2 plots
In previous chapters, you created a wide variety of general and specialized graphs (and had lots of fun in the process). Most were produced using R’s base graphics system. Given the diversity of methods available in R, it may not surprise you to learn that four separate and complete graphics systems are currently available.
In addition to base graphics, graphics systems are provided by the grid, lattice, and ggplot2 packages. Each is designed to expand on the capabilities of, and correct for deficiencies in, R’s base graphics system.
The grid graphics system provides low-level access to graphic primitives, giving programmers a great deal of flexibility in the creation of graphic output. The lattice package provides an intuitive approach for examining multivariate
437
438 |
CHAPTER 19 Advanced graphics with ggplot2 |
relationships through conditional one-, two-, or three-dimensional graphs called trellis graphs. The ggplot2 package provides a method of creating innovative graphs based on a comprehensive graphical “grammar.”
In this chapter, we’ll start with a brief overview of the four graphic systems. Then we’ll focus on graphs that can be generated with the ggplot2 package. ggplot2 greatly expands the range and quality of the graphs you can produce in R. It allows you to visualize datasets with many variables using a comprehensive and consistent syntax, and easily generate graphs that would be difficult to create using base R graphics.
19.1 The four graphics systems in R
As stated earlier, there are currently four graphical systems available in R. The base graphics system, written by Ross Ihaka, is included in every R installation. Most of the graphs produced in previous chapters rely on base graphics functions.
The grid graphics system, written by Paul Murrell (2011), is implemented through the grid package. grid graphics offer a lower-level alternative to the standard graphics system. The user can create arbitrary rectangular regions on graphics devices, define coordinate systems for each region, and use a rich set of drawing primitives to control the arrangement and appearance of graphic elements.
This flexibility makes grid graphics a valuable tool for software developers. But the grid package doesn’t provide functions for producing statistical graphics or complete plots. Because of this, the package is rarely used directly by data analysts and won’t be discussed further. If you’re interested in learning more about grid, visit Dr. Murrell’s Grid website (http://mng.bz/C86p) for details.
The lattice package, written by Deepayan Sarkar (2008), implements trellis graphs, as outlined by Cleveland (1985, 1993). Basically, trellis graphs display the distribution of a variable or the relationship between variables, separately for each level of one or more other variables. Built using the grid package, the lattice package has grown beyond Cleveland’s original approach to visualizing multivariate data and now provides a comprehensive alternative system for creating statistical graphics in R. A number of packages described in this book (effects, flexclust, Hmisc, mice, and odfWeave) use functions in the lattice package to produce graphs.
Finally, the ggplot2 package, written by Hadley Wickham (2009a), provides a system for creating graphs based on the grammar of graphics described by Wilkinson (2005) and expanded by Wickham (2009b). The intention of the ggplot2 package is to provide a comprehensive, grammar-based system for generating graphs in a unified and coherent manner, allowing users to create new and innovative data visualizations. The power of this approach has led ggplot2 to become an important tool for visualizing data using R.
Access to the four systems differs, as outlined in table 19.1. Base graphic functions are automatically available. To access grid and lattice functions, you must load the appropriate package explicitly (for example, library(lattice)). To access ggplot2 functions, you have to download and install the package (install.packages ("ggplot2")) before first use and then load it (library(ggplot2)).
|
An introduction to the ggplot2 package |
439 |
|
Table 19.1 Access to graphic systems |
|
|
|
|
|
|
|
System |
Included in base installation? |
Must be explicitly loaded? |
|
|
|
|
|
base |
Yes |
No |
|
grid |
Yes |
Yes |
|
lattice |
Yes |
Yes |
|
ggplot2 |
No |
Yes |
|
|
|
|
|
The lattice and ggplot2 packages overlap in functionality but approach the creation of graphs differently. Analysts tend to rely on one package or the other when plotting multivariate data. Given its power and popularity, the remainder of this chapter will focus on ggplot2. If you would like to learn more about the lattice package, I’ve created a supplementary chapter that you can download (www.statmethods
.net/RiA/lattice.pdf) or from the publisher’s website at www.manning.com/ RinActionSecondEdition.
This chapter uses three datasets to illustrate the use of ggplot2. The first is a data frame called singer that comes from the lattice package; it contains the heights and voice parts of singers in the New York Choral Society. The second is the mtcars data frame that you’ve used throughout this book; it contains automotive details on 32 automobiles. The final data frame is called Salaries and is included with the car package described in chapter 8. Salaries contains salary information for university professors and was collected to explore gender discrepancies in income. Together, these datasets offer a variety of visualization challenges.
Before continuing, be sure the ggplot2 and car packages are installed. You’ll also want to install the gridExtra package. It allows you to place multiple ggplot2 graphs into a single plot (see section 19.7.4).
19.2 An introduction to the ggplot2 package
The ggplot2 package implements a system for creating graphics in R based on a comprehensive and coherent grammar. This provides a consistency to graph creation that’s often lacking in R and allows you to create graph types that are innovative and novel. In this section, we’ll start with an overview of ggplot2 grammar; subsequent sections dive into the details.
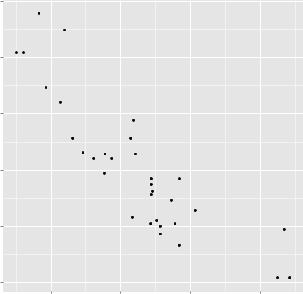
In ggplot2, plots are created by chaining together functions using the plus (+) sign. Each function modifies the plot created up to that point. It’s easiest to see with an example (the graph is given in figure 19.1):
library(ggplot2)
ggplot(data=mtcars, aes(x=wt, y=mpg)) + geom_point() +
labs(title="Automobile Data", x="Weight", y="Miles Per Gallon")
440 |
CHAPTER 19 Advanced graphics with ggplot2 |
Miles Per Gallon
Automobile Data
35
30
25
20
15
Figure 19.1 Scatterplot of
10
automobile weight by mileage
2 |
3 |
4 |
5 |
Weight
Let’s break down how the plot was produced. The ggplot() function initializes the plot and specifies the data source (mtcars) and variables (wt, mpg) to be used. The options in the aes() function specify what role each variable will play. (aes stands for aesthetics, or how information is represented visually.) Here, the wt values are mapped to distances along the x-axis, and mpg values are mapped to distances along the y-axis.
The ggplot() function sets up the graph but produces no visual output on its own. Geometric objects (called geoms for short), which include points, lines, bars, box plots, and shaded regions, are added to the graph using one or more geom functions. In this example, the geom_point() function draws points on the graph, creating a scatterplot. The labs() function is optional and adds annotations (axis labels and a title).
There are many functions in ggplot2, and most can include optional parameters. Expanding on the previous example, the code
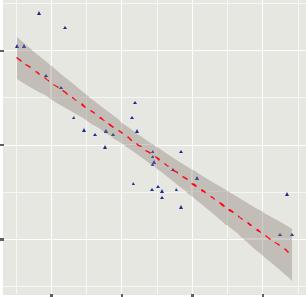
library(ggplot2)
ggplot(data=mtcars, aes(x=wt, y=mpg)) + geom_point(pch=17, color="blue", size=2) + geom_smooth(method="lm", color="red", linetype=2) +
labs(title="Automobile Data", x="Weight", y="Miles Per Gallon")
produces the graph in figure 19.2.
Options to geom_point() set the point shape to triangles (pch=17), double the points’ size (size=2), and render them in blue (color="blue"). The geom_smooth() function adds a “smoothed” line. Here a linear fit is requested (method="lm") and a red
An introduction to the ggplot2 package |
441 |
Automobile Data
|
30 |
|
|
|
Gallon |
|
|
|
|
Miles Per |
20 |
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
2 |
3 |
4 |
5 |
|
|
|
Weight |
|
Figure 19.2 Scatterplot of automobile weight by gas mileage, with a superimposed line of best fit and 95% confidence region
(color="red") dashed (linetype=2) line of size 1 (size=1) is produced. By default, the line includes 95% confidence intervals (the darker band). We’ll go into more detail about modeling relationships with linear and nonlinear fits in section 19.6.
The ggplot2 package provides methods for grouping and faceting. Grouping displays two or more groups of observations in a single plot. Groups are usually differentiated by color, shape, or shading. Faceting displays groups of observations in separate, side-by-side plots. The ggplot2 package uses factors when defining groups or facets.
You can see both grouping and faceting with the mtcars data frame. First, transform the am, vs, and cyl variables into factors:
mtcars$am <- factor(mtcars$am, levels=c(0,1), labels=c("Automatic", "Manual"))
mtcars$vs <- factor(mtcars$vs, levels=c(0,1), labels=c("V-Engine", "Straight Engine"))
mtcars$cyl <- factor(mtcars$cyl)
Next, generate a plot using the following code:
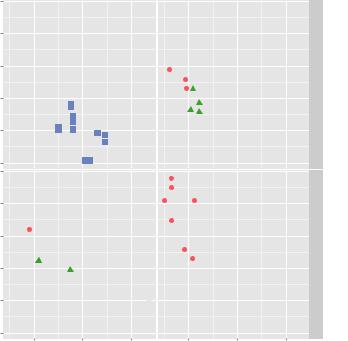
library(ggplot2) ggplot(data=mtcars, aes(x=hp, y=mpg,
shape=cyl, color=cyl)) + geom_point(size=3) + facet_grid(am~vs) +
labs(title="Automobile Data by Engine Type", x="Horsepower", y="Miles Per Gallon")
442 |
CHAPTER 19 Advanced graphics with ggplot2 |
Miles Per Gallon
35
30
25
20
15
10
35
30
25
20
15
10
Automobile Data by Engine Type
V−Engine |
|
Straight Engine |
Automatic
cyl
 4
4
 6
6
 8
8
Manual
|
|
|
|
|
|
|
|
100 |
200 |
300 |
100 |
200 |
300 |
||
Horsepower
Figure 19.3 A scatterplot showing the relationship between horsepower and gas mileage separately for transmission and engine type. The number of cylinders in each automobile engine is represented by both shape and color.
The resulting graph (see figure 19.3) contains separate scatterplots for each combination of transmission type (automatic vs. manual) and engine arrangement (V-engine vs. straight engine). The color and shape of each point indicates the number of engine cylinders in that car. In this case, am and vs are the faceting variables, and cyl is the grouping variable.
The ggplot2 package is powerful and can be used to create a wide array of informative graphs. It’s popular among seasoned R analysts and programmers; and, based on postings in R blogs and discussion groups, that popularity is growing.
Unfortunately, with power comes complexity. Unlike other R packages, ggplot2 can be thought of as a comprehensive graphical programming language in its own right. It has its own learning curve, and at times that curve can be steep. Hang in there—the effort is worth it. Luckily, there are function defaults and language simplifications designed to make your introduction to this package easier. With practice,
