7.11 Аналогочислові перетворення безперервного сигналу на базі теореми Котельникова в.А.

Теорема Котельникова во временном представлении.

Если функция не содержит составляющих с частотой выше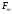Гц, то она полностью определяется последовательностью ее значений в точках, которые отстоятся на расстояние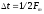сек. одна от другой. Сигнал заданный во временной области может быть однозначно отображен в частотной области и наоборот.

Пусть является спектром функциииограничена частотойF_м. Тогда

; .

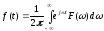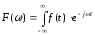Ввиду того, вне полосы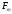, это выражение примет вид

.

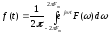Рассмотрим значения , которые удовлетворяют условию

,

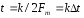где 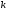- положительные или отрицательные числа. Для этих моментов времени выражение принимает вид

.

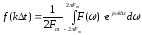Совокупность значений при всех положительных и отрицательных значениях определяет все коэффициенты ряда Фурье для.

Следовательно, этими значениями определяется и сама функция. Периодический сигнал может быть отображен рядом Фурье.

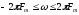Т.е. функция , задана на отрезкев ряде Фурье

,

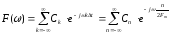Где коэффициент ряда Фурье

.

Следовательно,

.

Из приведенных уравнений видно, что

.

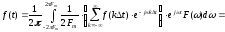
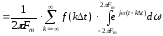В результате интегрирования получим

.

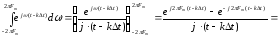
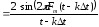Следовательно, будет справедливо выражение

;

.

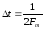С помощью полученного равенства может быть определена всюду по ее значениям в точках отсчета.

Это выражение может быть записано в следующем виде

,

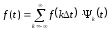где - функция отсчета.

Функция отсчета обладает рядом простых и важных свойств. Она равняется единице в одной точке отсчета и нулю во всех других точках. Спектр этой функции равномерный.

Элементарная функция Котельникова имеет в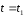значение, равное значению первого отсчетав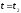равна значению второго отсчета и так далее. В остальные отсчетные моменты времени эти функции равны нулю. Сумма элементарных функций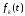дает исходную непрерывную функцию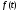

Теорема Котельникова используется и в частотном представлении. Эта теорема формулируется следующим образом.

Если функция 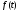тождественно равна нулю вне интервала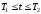, то ее спектр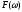однозначно определяется последовательностью его составляющих точек, отстоящих друг от друга на.

Докажем это.

Спектральное представление функции 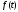имеет вид

.

Разложим функцию в ряд Фурье в интервале от до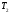

,

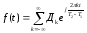где ,

где .

Следовательно, .

Подставим это выражение в формулу для

.

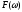
После интегрирования получим

,

где .

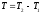Это выражение запишем в виде

.

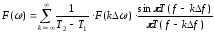Теорема доказана.

Теорема Котельникова применяется при квантовании по времени непрерывного сигнала если его спектр располагается в области и ширина спектра. Для узкополосных сигналов характерно неравенство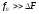, где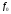- несущая частота. Поскольку при этом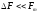, непосредственно применять теорему Котельникова нецелесообразно. В этом случае перед квантованием сигнала по времени осуществляют преобразование спектра этого сигнала с целью переноса его в область низких частот.

7.12 Пропускна спроможність двійкового каналу зв’язку з перешкодами та без перешкод.

Пропускная способность канала святи без помех

Будем рассматривать канал передачи двоичных сигналов, когда любое сообщение является кодовой комбинацией из символов «0» и «1». Длительность сигналов «0» и «1» одинакова и равна Тс=1/В, где В – скорость модуляции.

Основные определения:

1. Средняя скорость передачи сообщений V (сообщ/сек) – среднее число символов, что передаются по каналу за одну секунду.

2. Скорость передачи информации С1 (бит/сек) – количество информации, что передается за одну секунду.

3. Пропускная способность канала С (бит/сек) – максимальное количество информации, что передается по данному каналу за секунду, т.е. С=С1макс.

При анализе дискретного канала без помех единственным показателем является наиболее эффективное использование пропускной способности канала.

Величина С1 характеризует среднее количество информации, что передается за секунду и определяется равенством: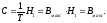

Тут Н(х) и Iх соответственно означают среднюю неопределенность и среднее количество информации при приёме сообщений длительностью Т. Если Т стремится к бесконечности то для определения средней скорости необходимо учитывать всю совокупность возможных сообщений. Будем считать что скорость передачи информации постоянна, и т.о. справедливо равенство: С₁=Н(х)/Т, при любом конечном Т.

Максимальное количество двоичных символов В_макс, что могут быть отправлены по каналу за 1 сек., зависит от электрических характеристик канала. Пропускная способность канала будет полностью использована, если среднее количество информации на один двоичный символ будет максимально. В этом случае для передачи сообщений будет нужно минимальное количество двоичных символов, и средняя длинна сообщения будет минимальна. Этого можно достигнуть , если символы «0» и «1» будут равномерными и независимыми друг от друга. В таком случае энтропия источника сообщений на один символ равна:

Н₁=log₂2=1 бит/сек. Это максимальное количество информации, что может нести один двоичный символ. Тогда пропускная способность канала для передачи двоичных символов без помех равно количеству элементарных посылок «0» и «1», что могут быть отправлены по каналу за 1 сек.

Пропускная способность канала святи с помехами

Существует два варианта определения пропускной способности канала с помехами:

1. Максимальное количество информации передаваемой по каналу с вероятностью ошибки не более некой допустимой величины.

2. Максимальное количество информации передаваемой по каналу передается абсолютно верно

При наличии помех среднее количество информации, что содержится в одном принятом элементарном сообщении равно:

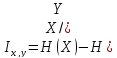
В таком случае скорость передачи информации по дискретному каналу без помех:

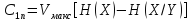
где 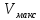– максимальное количество независимых сообщений, что может быть в среднем передано по каналу за 1 секунду.

Если свойства канала определяются как 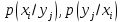то максимальную скорость передачи можно обеспечить путем выбора определенных ограничений, а именно оптимальное распределение вероятности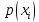, то есть путем выбора оптимального ансамбля сигналов. Относительно этого пропускная способность дискретного канала с помехами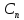как максимальную скорость передачи информации, что может быть достигнута при заданих свойствах канала, то есть:

Где максимум берется по всем допустимым распределениям вероятности .

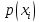Выражение пропускной способности 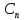может быть написано в нескольких формах. Можно записать: