7.3. Алгоритми оптимальної обробки при розрізненні двійкових сигналів.

Алгоритмы оптимальной обработки при различении двоичных сигналов. Критерии оценки помехоустойчивости.

В реальных системах связи прием осуществляется в условиях влияния помех. Это приводит к искажению сигнала, которое имеет случайный характер и усложняет процесс различения этих сигналов.

При оценке помехоустойчивости систем передачи информации анализ проводят с точки зрения обеспечения верности передачи сообщений по каналу связи, которая нужна, при заданных уровнях и характере сигнала и помех.

Количественная оценка помехоустойчивости системы передачи информации может быть проведена по степени соответствия принимаемых сообщений переданным в заданных условиях приема.

Оптимальным является приемное устройство, которое обеспечивает при заданном критерии оптимальности максимальную степень соответствия принимаемых сообщений переданным, т.е. высочайшую помехоустойчивость. Эту предельно достижимую в заданных условиях приема помехоустойчивость называют потенциальной помехоустойчивостью.

Прием двоичных сигналов представляет собой в общем случае статистическую задачу различения двух сигналов хотя бы по одному из его параметров (амплитуде, частоте, фазе и т.д.) при наличии помех.

Пусть на вход приемного устройства поступает смесь напряжений сигнала 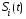и флуктуационной помехи:

,

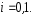
Чем больше априорная информация о параметрах сигналов, тем больше вероятность их правильного различения. В данном случае рассматривается ситуация, при которой все параметры сигналов (в том числе и их фазы) точно известны. По результатам наблюдения за реализацией принятого колебания необходимо с учетом критерия оптимальности определить, который из двух возможных символов 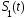или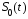фактически передавался.

Совокупность возможных реализаций принятых колебаний 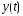образует пространство принимаемых сигналов.

Сигналы 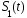иизображены в этом пространстве соответствующими точками.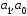

Каждой из возможных реализаций принятого сигнала отвечает определенная точка в пространстве сигналов, которая в общем случае не совпадает с 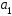или.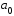

Разобьем пространство сигналов на две области, которые не перекрещиваются, каждая из которых соответствует принятию определенной гипотезы о том, что сигнал (или соответствующий ему символ 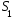или) был передан.

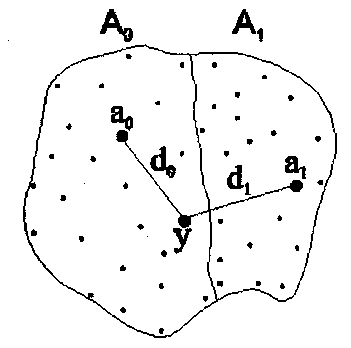(рис 1)

Под влиянием помех принятый сигнал может оказаться в другом подмножестве, что приведет к возникновению ошибки. По принятой реализации можно лишь судить о величине вероятности, какой был передан символ:или.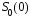

Поэтому максимум, что можно потребовать от приемника - это определить условные вероятности и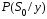, если будет известный принятый сигнал

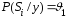Критерий Котельникова требует, чтобы всякий раз при приеме колебания выносилось решение, что передавался сигнал, для которого апостериорная вероятностьимеет максимальное значение. Функциональная схема обработки сигналов в соответствии с этим критерием содержит устройства вычисленияи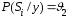, а также устройство сравнения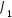и. Для двоичных сигналов правило решения сводится к проверке неравенства

. (1)

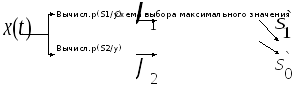
Схема отработки сигналов (рис 2)

При выполнении неравенства (1) регистрируется символ "1" (верна гипотез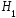а ), в противном случае "0" (гипотеза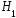- ошибочна).

Вычисление 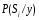выполняется на основе известной формулы Байеса

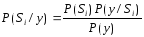, (2)

где - вероятность приема реализации

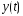
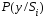- вероятность приема 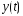при условии, что передан полезный сигнал,

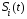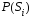- априорная вероятность передачи символа

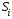
Так как приемник должен производить сравнение при данном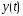и различных, то постоянный при этом сравнении множитель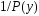в правой части уравнения (2) значения не имеет и вместо значенийможно сравнивать величины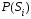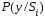, то есть:

Тогда:

.

Левая часть этого выражения называется отношением правдоподобия, его обозначают . В случае, если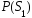=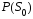, приведенное правило упрощается:

.

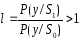Поскольку в принятой реализации может содержаться только или, то.

Если 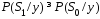, то за переданный принимается, тогда вероятность ошибки

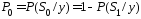
т.е. вероятность ошибки минимальна, если максимальна апостериорная вероятность 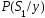. Это означает, что критерий эквивалентен критерию минимума вероятности ошибки:

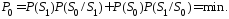
При передаче данных справедливо равенство 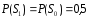. В этом случае получим

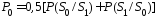. (3)

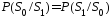
При 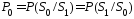. Каналы, в которых соблюдается данное равенство, называются симметричными.

Критерий минимума вероятности ошибки часто называют критерием идеального наблюдателя Котельникова.

Рассмотренные критерии оценки помехоустойчивости по максимуму апостериорной вероятности и минимуму вероятности ошибки используются при передаче дискретных сообщений в системах связи, когда любые ошибочные переходы одинаково нежелательны.

Вместе с тем, имеются системы, в которых ошибочные переходы являются неравнозначными. Это различие учитывается критерием Неймана- Пирсона, на основе которого можно, задав некоторую допустимую величину вероятности 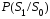, обеспечить минимальную вероятность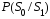. В тех случаях, когда априорные вероятности появления сигналов неизвестны, задачу оптимизации решают на основеминимаксного критерия, доставляющего минимальное значение максимального риска. В технических приложениях встречаются и другие критерии, учитывающие последствия правильного и ошибочного принятия статистических гипотез 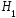и.

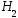Принимая во внимание, что при заданном детерминированном сигнале значение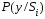можно заменить плотностью вероятности, отношение правдоподобия можно записать в виде

.

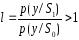Геометрический смысл критерия отношения правдоподобия при приеме двоичных полностью известных сигналов заключается в том, что переданным должен считаться тот символ, точка отображающая (,) находится ближе к точке у, которая отображает реализацию принятого колебания(рис 1).

Итак, решающее правило для оптимального приемника можно записать в виде:

В соответствии с этим правилом приемное устройство должно поделить все пространство сигналов на два непересекающихся подпространства сигналов А₁ и А₀; определить, в какой области находится точка у. Если она находится в подпространстве А₁, то принимается решение, что передавалась 1, в противном случае – 0.

Указанное правило принятия решения можно записать следующим образом: .рис 3

Это неравенство определяет алгоритм оптимального приемника Котельникова, обеспечивающего минимум средней вероятности ошибки (рис. 3). Если энергия сигналов 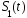и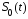одинаковы, неравенство, приведенное выше, можно представить в виде корреляционных интегралов

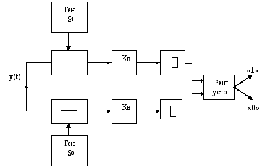
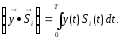
Структурная схема корреляционного приемника Котельникова представлена на рис. 4. По существу корреляционный приемник является активным фильтром и выполняет операцию скалярного произведения рис 4