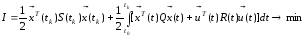- •1.1. Поняття операційної системи.
- •1.5. Поняття асемблера, компілятора, транслятора, інтерпретатора.
- •1.6. Завантажувачі. Завдання завантажувачів. Принципи побудови завантажувачів.
- •1.7. Принципи об’єктно-орієнтованого програмування (парадигми програмування, поняття класу).
- •1.8. Наслідування (Просте наслідування. Множинне наслідування).
- •1.9. Інкапсуляція. Поняття, сфери застосування.
- •1.10. Поліморфізм. Поняття, сфери застосування.
- •1.11. Принципи розробки розподілених клієнт-серверних програм. Особливості розробки мережевих програм з використанням сокетів.
- •2.1 Багаторівнева комп’ютерна організація – структура й призначення рівнів.
- •2.2 Схема комп’ютера з єдиною шиною. Основні характеристики та принципи роботи шини комп’ютера.
- •2.3 Структура процесора, внутрішні блоки, види регістрів.
- •2.4 Команди процесора, структура команд. Цикл Фон-Неймана.
- •2.5 Структуру пам’яті комп’ютера. Елементи статичної та динамічної пам’яті.
- •2.6 Переривання, типи, алгоритм обробки переривання процесором.
- •2.7 Організація оперативної пам’яті, адресний простір, сегменти пам’яті, дескриптори сегментів.
- •3.1 Загальні відомості з теорії систем. Класифікація систем.
- •3.2 Поняття вимірювальної шкали. Види шкал.
- •3.3 Показники якості та ефективності та крітерії їх оцінювання.
- •3.4 Вирішення багатокрітеріальних задач.
- •3.5 Вирішення задачі вибору.
- •3.6 Декомпозиція. Компроміси між повнотою та простотою.
- •3.7 Агрегування. Види агрегування.
- •3.8 Поняття експертних методів. Експертні системи.
- •4.1. Методи розрахунку часових параметрів і критичних шляхів мережевої моделі проекту. Табличний метод.
- •4.2. Методи розрахунку часових параметрів і критичних шляхів мережевої моделі проекту. Матричний метод визначення часових параметрів.
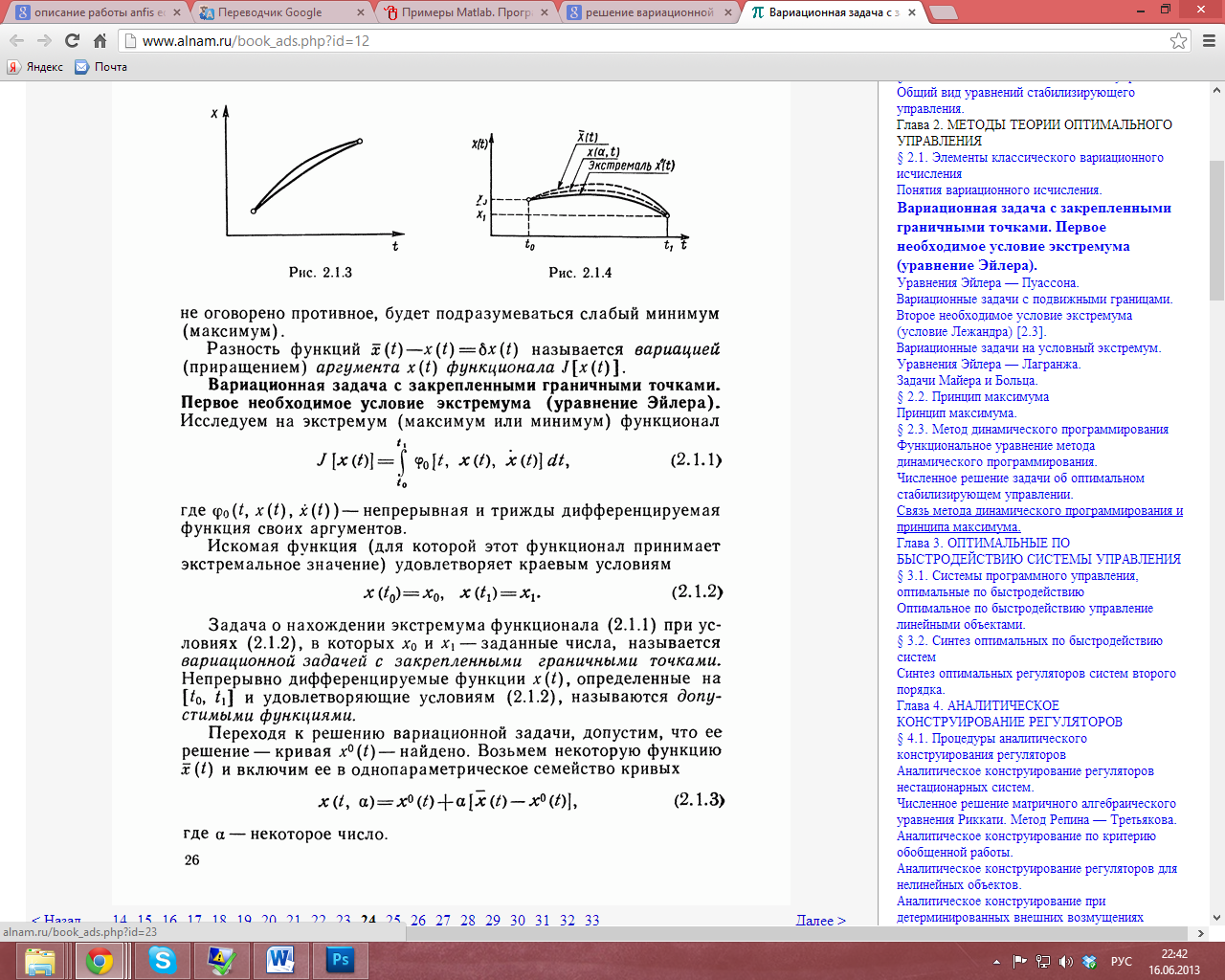
- •4.3. Метод класичного варіаційного числення. Рішення варіаційної задачі із закріпленими граничними крапками.
- •4.4. Метод класичного варіаційного числення. Рівняння Ейлера-Лагранжа.
- •4.5. Постановка задачі оптимального управління. Класифікація задач оптимального управління.
- •4.6. Характеристика керованості і спостережності. Постановка завдання. Критерії керованості і спостережності.
- •6.1 Основні теоретико-множинні (об’єднання, пересічення, віднімання, декартовий добуток) операції реляційної алгебри. Коротка характеристика та приклади.
- •6.2. Основні нормальні форми. Характеристика і приклади відносин, що знаходяться в 1нф, 2нф, 3нф.
- •Id, category, product1, product2, product3
- •6.3. Основні оператори мови маніпулювання даними. Оператор вибірки даних (одно- і багатотабличні запити оператора select).
- •7.2) Модели детерминированных цифровых сигналов
- •7.3. Алгоритми оптимальної обробки при розрізненні двійкових сигналів.
- •7.4. Потенціальна завадостійкість при прийомі ам, чм та фм сигналів.
- •7.5. Багатократні та комбіновані методи модуляції.
- •7.6. Методи боротьби з помилками, що виникають в каналах зв’язку. Завадостійке кодування.
- •7.7 Основні параметри завадостійких кодів. Принципи виявлення та виправлення помилок.
- •7.8 Циклічні коди. Згортальні коди.
- •7.9 Статичні методи стиснення інформації Алгоритм арифметичного стиснення.
- •7.10 Оптимальне кодування інформації. Алгоритми формування коду Хофмана та Шенона-Фано.
- •7.11 Аналогочислові перетворення безперервного сигналу на базі теореми Котельникова в.А.
- •7.12 Пропускна спроможність двійкового каналу зв’язку з перешкодами та без перешкод.
- •8.1. Протоколи фізичного рівня.
- •8.2. Характеристика лінійних сигналів, що використовуються в комп’ютерних мережах.
- •8.4. Загальні характеристики канального рівня.
- •8.5. Протокол hdlc.
- •8.6. Методи доступу в мережу.
- •8.7. Протокол ip. Адресація в ip-мережах.
- •8.8. Протокол tcp.
- •9.1 Алгоритм принятия решения по управлению кс
- •9.2. Архітектура систем управління комп’ютерними мережами.
- •9.3. Управління потоком інформації шляхом раціонального вибору параметрів протоколу.
- •9.4. Управління обслуговуванням різнорідного трафіку: дисципліни обслуговування, їх переваги та недоліки.
- •9.5. Управління якістю обслуговування. Забезпечення якості обслуговування шляхом управління мережевими ресурсами.
- •9.6. Основні стандарти управління комп’ютерними мережами. Мережеве управління за стандартом tmn: визначення, функціональні області, інтерфейси.
- •9.7. Модель управління протоколів snmp та cmip: структура, стандартизовані елементи, переваги та недоліки.
- •10.1. Основні концепції побудови обчислювальних систем, що самоорганізуються.
- •10.2. Класифікація процесорів по архітектурі системи команд (cisc, risc).
- •10.3. Показники ефективності паралельних часових моделей алгоритмів.
- •10.4. Основні ознаки класифікації Флинна. Фрагмент класифікації Флинна.
- •10.5. Відмінності командної чарунки в vliw-процесорі від командної чарунки процесора з послідовною обробкою даних.
- •11.1Стадії та етапи створення асу тп.
- •11.2 Склад і коротка характеристика розділів технічного проекта.
- •11.3 Склад і зміст проектних рішень з технічного забезпечення.
- •11.4Склад і задачі організацій, що беруть участь у роботах зі створення асу тп.
- •11.5Перелік видів випробувань асу тп та їх короткий зміст.
- •11.6 Розрахунок вартості проектних робіт ресурсним методом.
- •11.7 Застосування елементних кошторисних норм для розрахунку вартості пусконалагоджувальних робіт.
4.3. Метод класичного варіаційного числення. Рішення варіаційної задачі із закріпленими граничними крапками.


4.4. Метод класичного варіаційного числення. Рівняння Ейлера-Лагранжа.
Уравнения Эйлера — Лагранжа являются основными формулами вариационного исчисления, c помощью которых ищутся стационарные точки и экстремумы функционалов. В частности, эти уравнения широко используются в задачах оптимизации, и, совместно с принципом стационарности действия, используются для вычисления траекторий в механике. В теоретической физике вообще это (классические) уравнения движения в контексте получения их из написанного явно выражения для действия (лагранжиана).
Использование уравнений Эйлера — Лагранжа для нахождения экстремума функционала в некотором смысле аналогично использованию теоремы дифференциального исчисления, утверждающей, что лишь в точке, где первая производная функции обращается в нуль, гладкая функция может иметь экстремум.
Пусть задан функционал
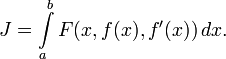
с
подынтегральной функцией ![]() ,
обладающей непрерывными первымичастными
производнымии называемойфункцией
Лагранжа, где черезf' обозначена
первая производная f по x.
Если этот функционал достигает экстремума
на некоторой функции
,
обладающей непрерывными первымичастными
производнымии называемойфункцией
Лагранжа, где черезf' обозначена
первая производная f по x.
Если этот функционал достигает экстремума
на некоторой функции ![]() ,
то для неё должно выполнятьсяобыкновенное
дифференциальное уравнение
,
то для неё должно выполнятьсяобыкновенное
дифференциальное уравнение
![]()
которое называется уравнением Эйлера — Лагранжа.
Существует также множество многомерных вариантов уравнений Эйлера — Лагранжа.
Если
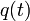 —
путь в
—
путь в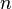 -мерном
пространстве, то он доставляет экстремум
функционалу
-мерном
пространстве, то он доставляет экстремум
функционалу
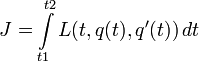
только если удовлетворяет условию
![]()
![]()
В
физических приложениях
когда ![]() являетсялагранжианом(имеется
в виду лагранжиан некоторой физической
системы; то есть еслиJ — действиедля
этой системы), эти уравнения — суть
(классические) уравнения движения такой
системы. Это утверждение может быть
прямо обобщено и на случай бесконечно
мерногоq.
являетсялагранжианом(имеется
в виду лагранжиан некоторой физической
системы; то есть еслиJ — действиедля
этой системы), эти уравнения — суть
(классические) уравнения движения такой
системы. Это утверждение может быть
прямо обобщено и на случай бесконечно
мерногоq.
Другое многомерное обобщение получается при рассмотрении функции
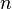 переменных.
Если
переменных.
Если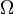 —
какая-либо, в данном случаеn-мерная,
поверхность, то
—
какая-либо, в данном случаеn-мерная,
поверхность, то
![]()
где ![]() —
независимые координаты,
—
независимые координаты,![]() ,
,![]() ,
,
доставляет
экстремум если только ![]() удовлетворяетуравнению
в частных производных
удовлетворяетуравнению
в частных производных
![]()
Если ![]() и
и![]() —
функционал энергии, то эта задача
называется «минимизацией поверхности
мыльной плёнки».
—
функционал энергии, то эта задача
называется «минимизацией поверхности
мыльной плёнки».
Очевидная комбинация двух описанных выше случаев используется для получения уравнений движения распределенных систем, таких как физические поля, колеблющиеся струны или мембраны и т.п.
4.5. Постановка задачі оптимального управління. Класифікація задач оптимального управління.
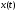 -
значение к-го в каждый момент времени
описания некоторой физ. системы.
-
значение к-го в каждый момент времени
описания некоторой физ. системы.

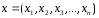
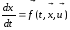 ,
,
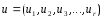 (1) - вектор управления
(1) - вектор управления
Вектор фазовой траектории.
Могут быть наложены ограничения в виде равенств и неравенств.
 (2)
(2)
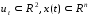
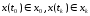 (3)
(3)
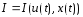 (4)
(4)
При
заданных уравнениях объекта управления
(1), ограничениях(2) и краевых условий(3)
требуется найти такие управления
 и
фазовую траекторию х*(t), при которых
показатель качества I принимал бы min или
max значения.
и
фазовую траекторию х*(t), при которых
показатель качества I принимал бы min или
max значения.
Требования к показателю качества управления:
- должен иметь прямое отношение к существу задачи;
- должен быть критичным по отношению к тем параметрам, значения которых следует определить;
- должен быть наиболее простым из всех обладающих должной критичностью.

Задача Больца:
 (5)
(5)
Задача Лагранжа:
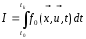 (6)
(6)
Задача Майера:
 (7)
(7)
Общий
вид:
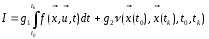
Если
записать ЗМ
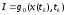 ,
то ее называют задачей терминального
управления.
,
то ее называют задачей терминального
управления.
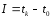 -
задача максимального быстродействия
-
задача максимального быстродействия
Для следящих систем ЗЛ:
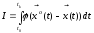

Q – зад., неотр. опред. сим. (часто диагональная) матрица весовых коэф.(матрица штрафов за ошибки)
XT – 1*n
X – n*1
(1*n)(n*n)(n*1)=число
(1*n)(m*n), если m=n
(n*1)(1*n)=n*n
Задача на min энергии:
Ф-л зависит только от управления, в этом случае:

Оптимальный линейный регулятор