2.3. Решение систем линейных уравнений методом обратной матрицы
Метод обратной матрицы – это метод решения квадратных систем линейных уравнений, в которых определитель системы не равен нулю.
Рассмотрим систему:
Обозначим
через
матрицу коэффициентов при неизвестных,
через
и
– матрицы-столбцы переменных и правой
части.
;
;
;
.
Систему уравнений можно представить в матричной форме, она примет такой вид:
.
Умножим это равенство на обратную матрицу
,
,
Мы
получили матричную запись решения
системы линейных уравнений, из которой
можно заключить следующее: чтобы
квадратную систему линейных уравнений
решить методом обратной матрицы,
необходимо найти обратную матрицу и
умножить ее “слева” на матрицу-столбец
.
Пример 9. Решить систему методом обратной матрицы
.
Ранее
мы нашли обратную для матрицы
– в примере 8.
,
,
.
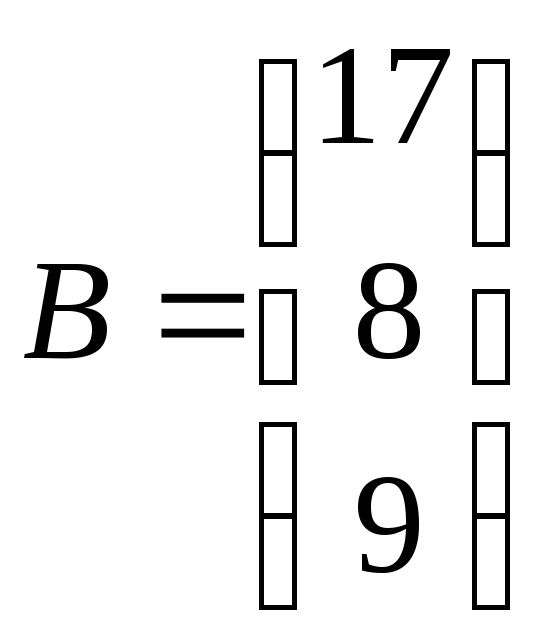
Проверка показывает, что система решена верно.
2.4. Метод Гаусса для решения систем линейных уравнений
Метод Гаусса является универсальным методом решения систем линейных уравнений. Он заключается в приведении системы к треугольному виду путем последовательного исключения неизвестных и реализуется в несколько этапов:
I
этап– выбирается первое ведущее
уравнение, содержащее
,
и с его помощью из всех остальных
уравнений исключается
.
II
этап– первое ведущее уравнение
остается неизменным; выбирается второе
ведущее уравнение из всех оставшихся
и с его помощью исключается неизвестная
;
III
этап– первое и второе ведущие
уравнения остаются неизменными.
Выбирается третье ведущее и с его помощью
исключается
и т.д.
Когда система приведена к треугольному виду, то, двигаясь в обратном порядке, находят значения неизвестных величин.
Пример 10. Решить систему методом Гаусса.
В качестве первого ведущего выбираем второе уравнение, т.к. у него первый коэффициент равен единице.
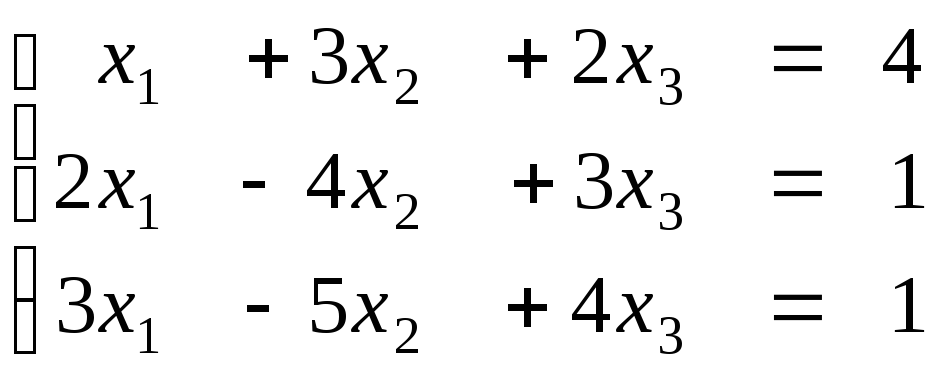
І
этап
ІI
этап
Из
третьего уравнения определяем:
;
из второго:
,
,
;
из первого:
.
Таким образом,
.
Замечание. Очень удобной модификацией метода Гаусса является правило прямоугольника, которое тоже реализуется поэтапно.
Пример 11. Рассмотрим систему и решим ее модифицированным методом Гаусса.
Идея
подхода прежняя – расширенная матрица
приводится к треугольному виду. Она
составляется с участием правой части
системы
и контрольного столбца
:
Элементы контрольного столбца равны сумме всех элементов соответствующих строк.
I этап.Считаем первый диагональный элемент не равным нулю (в противном случае поменяет местами строки). Этот элемент назовемпервым генеральным элементом. В данном случае – это число 2. Далее первую строку переписываем без изменения, а первый столбец дополняем нулями. Остальные элементы определяем по правилу прямоугольника. Чтобы построить прямоугольник, каждый элемент соединяют с первой строкой и первым столбцом, а затем – с генеральным элементом. Вычисления проводят так: из произведения элементов диагонали, содержащей генеральный элемент, вычитают произведение элементов второй диагонали. В результате указанных преобразований получим:
Контрольный столбец, вычисленный по правилу прямоугольника, по-прежнему должен равняться сумме элементов строки.
II этап.Вторым генеральным элементом будет второй диагональный элемент. Далее первую и вторую строки переписываем без изменения, а первый и второй столбец дополняем нулями. Остальные элементы находим по правилу прямоугольника.
Сократим третью строку на 2, а четвертую – на (– 2).
III этап.Выбираем третий генеральный элемент – он третий по диагонали. Три строки оставляем без изменения, три столбца дополняем нулями, остальные элементы – по правилу прямоугольника.
Матрица приведена к треугольному виду. Контрольный момент проверен. Начиная с последней строки, определим неизвестные.
,
,
,
,
,
,
,
,
.
Проверка:
