лінійної регресії, коли вибіркове рівняння регресії Y на X має такий вигляд:

yx = a × x + b.

У цьому випадку для точкових оцінокa і b можна побудувати довірчі інтервали і оцінити їх значущість.

Основним методом отримання точкових оцінок для параметрів a

і b рівняння регресії є метод найменших квадратів.

3.9.4. МЕТОД НАЙМЕНШИХ КВАДРАТІВ

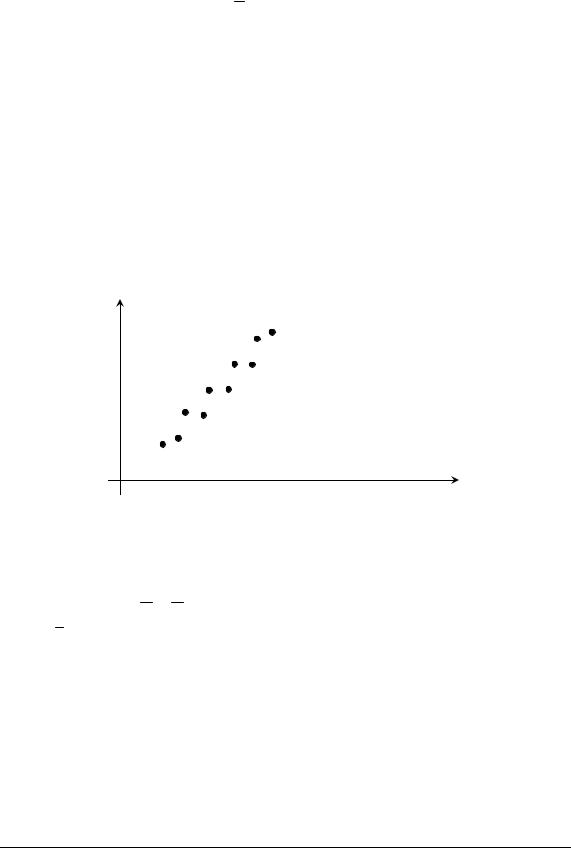
Припустимо, що вибірка (x1, y1 ), (x2 , y2 ), ... , (xn , yn ) обсягу n – не згрупована. Оскільки ми припустили існування лінійного зв’язку між результативною та факторною ознаками, то діаграма розсіювання точок (xi , yi ) має вигляд:

y

Рис. 3.3. Діаграма розсіювання точок

Основна ідея методу найменших квадратів полягає в тому, що точ-

ковими оцінками a і b параметрів a і b вибирають такі числа, для яких пряма yx =a x + b є “найближчою” до точок (x1, y1), (x2 , y2 ), K, (xn , yn ).

Мірою відхилення шуканої прямої від точок(xi , yi ) вибирають величину:

n

S (a, b ) = å[ yi - (a xi + bi )] 2 ,

i =1

тобто суму квадратів різниць між ординатами прямої та ординатами точок (xi , yi ) для одних і тих самих значень x = xi .

ДВНЗ “Українська академія банківської справи НБУ”

129

Якщо числа a і b – такі, що функція S (a, b ) має найменше значення, то пряма y x = a x + b найменше відхиляється від точок (xi , yi ).

Методом найменших квадратів називається метод знаходження статистичних оцінок a і b параметрів a і b за допомогою функції S (a, b ), виходячи з рівності:

S(a, b) = min S(a, b).

Для знаходження мінімуму функції S (a, b ) маємо розв’язати систему рівнянь:

яку елементарними перетвореннями зводимо до такого вигляду:

У випадку згрупованої вибірки для визначення невідомих параметрів a і b маємо систему двох рівнянь:

x1, x2 , ..., xn обов’язково є різні числа, робимо висновок про визначник системи:

130

Звідси випливає, що досліджувана система рівнянь має єдиний розв’язок:

Таким чином, шукане рівняння регресії набуває такого вигляду:

yx = a x + b.

Коефіцієнт a називають коефіцієнтом регресії, який характеризує відношення величини приросту результативної ознакиD y x до

величини приросту факторної ознаки Dx.

Лінійне рівняння регресії можна подати в іншому вигляді через статистичну оцінку коефіцієнта кореляції:

y- y = r* s y (x - x).

xxy s x

Необхідно зауважити, що в разі порушення припущення про лінійність зв’язку між результативною та факторною ознаками, про це можна зробити висновок із діаграми розсіювання вибірки, використовують нелінійні регресійні моделі. У нелінійних регресійних моделях зв’язок може виражатися, наприклад, такими рівняннями:

y x = ax2 + bx + c або y x = ax3 + bx2 + cx + d або y x = a / x + b. Статис-

тичні оцінки параметрів у цих нелінійних моделях також можна знайти за допомогою методу найменших квадратів.

Приклад 3.12. Знайти рівняння регресії Y на X на підставі вибірки:

DB ( X ) = 0,1 (1,22 +1,52 +K + 6,32 ) - 3,172 = 2,7921; s X = 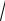2,7921 =1, 671.

DB (Y ) = 0,1 (5,62 + 6,82 +K+18,52 ) -11,272 =15,146; sY = 15,146 = 3,892.

ДВНЗ “Українська академія банківської справи НБУ”

131

Для обчислення вибіркового коефіцієнта кореляції обчислимо по-

10

передньо: åxi yi = 1,2 × 5,6 +1,5 × 6,8 + ... + 6,3 ×18,5 = 420,38.

Питання для самоконтролю

1.Яке рівняння називається вибірковим рівнянням регресіїY на X ?

2.Який метод є основним методом отримання точкових оцінок для параметрів рівняння регресії, у чому він полягає?

3.Що називають коефіцієнтом регресії?

4.Якими рівняннями може виражатися зв’язок між випадковими -ве личинами в нелінійних регресійних моделях?

5.За допомогою якого методу можна дістати статистичні оцінки -па раметрів нелінійних регресійних моделей?

Вправи

1.Знайти вибіркове рівняння регресіїY на X за даними вправи1 з пункту 3.9.2.

2.Знайти вибіркові рівняння регресіїY на X та X на Y за даними вправи 2 з пункту 3.9.2.

3.На хімічному виробництві отримані такі дані про залежність виходу готового хімічного продукту Y (кг/год.) від температури реакції X (°С):

місце лінійна модель.

4.За допомогою методу найменших квадратів скласти емпіричне рівняння прямої регресії залежності випадкової величини Y від випадкової величини X на підставі вибірки вправи 3 з пункту 3.9.2.

ДВНЗ “Українська академія банківської справи НБУ”

132