Базовий мінор матриці. Ранг матриці.

Як було сказано вище, мінором матриці порядкуsназивається матриця, утворена з елементів вихідної матриці, що перебувають на перетині яких-небудь обранихsрядків іsстовпців.

Визначення.У матриці порядкуmnмінор порядкуrназиваєтьсябазовим, якщо його визначник не дорівнює нулю, а всі мінори порядкуr+1 і вище дорівнюють нулю, або не існують зовсім, тобтоrзбігається з меншим із чиселmабоn.

Стовпці й рядки матриці, на яких стоїть базовий мінор, також називаються базовими.

У матриці може бути кілька різних базових мінорів, що мають однаковий порядок.

Визначення.Порядок базового мінору матриці називаєтьсярангом матриці й позначається RankА.

Дуже важливою властивістю елементарних перетвореньматриць є те, що вони не змінюють ранг матриці.

Визначення. Матриці, отримані в результаті елементарного перетворення, називаються еквівалентними.

Треба відзначити, що рівні матриці й еквівалентні матриці – поняття зовсім різні.

Теорема.Найбільше число лінійно незалежних стовпців у матриці дорівнює числу лінійно незалежних рядків.

Оскільки елементарні перетворення не змінюють ранг матриці, то можна істотно спростити процес знаходження рангу матриці.

Приклад.Визначити ранг матриці.

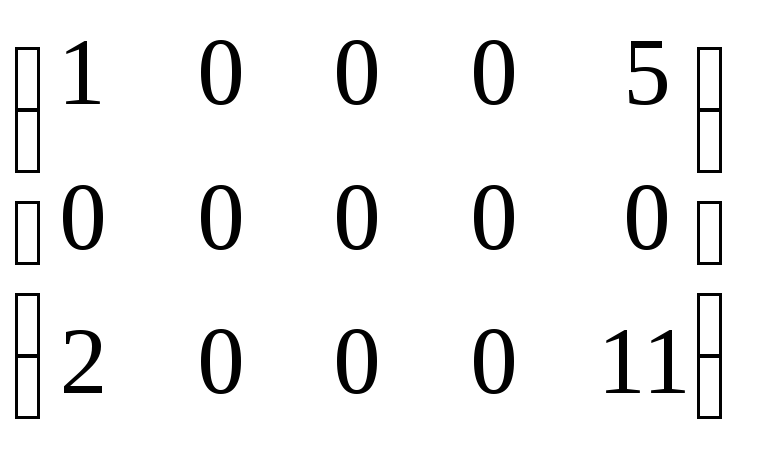
,RankA= 2.

Приклад:Визначити ранг матриці.

,RankA= 2.

Приклад.Визначити ранг матриці.

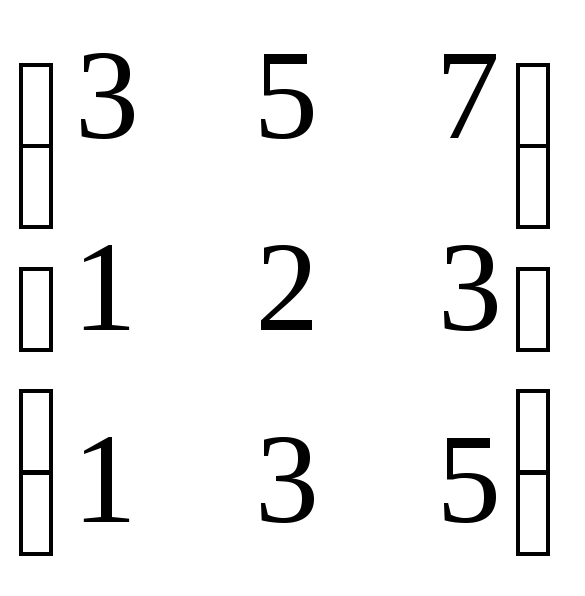
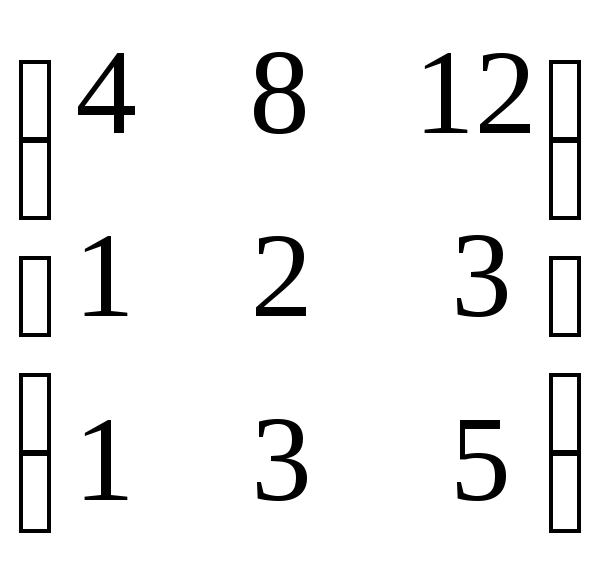
,RankA= 2.

Якщо за допомогою елементарних перетворень не вдається знайти матрицю, еквівалентну вихідній, але меншого розміру, то знаходження рангу матриці варто починати з обчислення мінорів найвищого можливого порядку. У вищенаведеному прикладі – це мінори порядку 3. Якщо хоча б один з них не дорівнює нулю, то ранг матриці дорівнює порядку цього мінору.

Теорема про базовий мінор.

Теорема. У довільній матриці А кожний стовпець (рядок) є лінійною комбінацією стовпців (рядків), у яких розташований базовий мінор.

Таким чином, ранг довільної матриці А дорівнює максимальному числу лінійно незалежних рядків (стовпців) у матриці.

Якщо А– квадратна матриця й detА= 0, то принаймні один зі стовпців – лінійна комбінація інших стовпців. Те ж саме справедливе й для рядків. Дане твердження слід із властивості лінійної залежності при визначнику рівному нулю.

Матричний метод розв’язання систем лінійних рівнянь.

Матричний метод застосуємо до розв’язання систем рівнянь, де число рівнянь дорівнює числу невідомих.

Метод зручний для розв’язання систем невисокого порядку.

Метод заснований на застосуванні властивостей множення матриць.

Нехай дана система рівнянь:

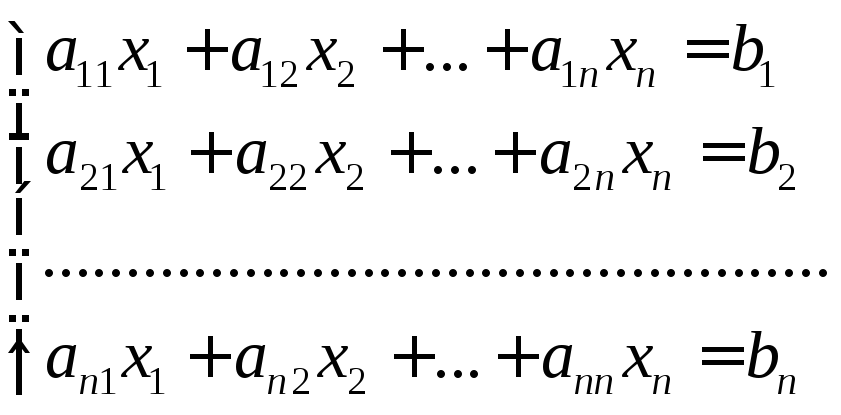
Складемо матриці: A=;B=;х=.

Систему рівнянь можна записати:

Aх=B.

Зробимо наступне перетворення: A^–1Aх=A^–1B,

оскільки А^–1А=Е, тоЕх=А^–1В

х = А^–1В

Для застосування даного методу необхідно знаходити обернену матрицю, що може бути пов'язане з обчислювальними труднощами при розв’язанні систем високого порядку.

Приклад.Розв’язати систему рівнянь:

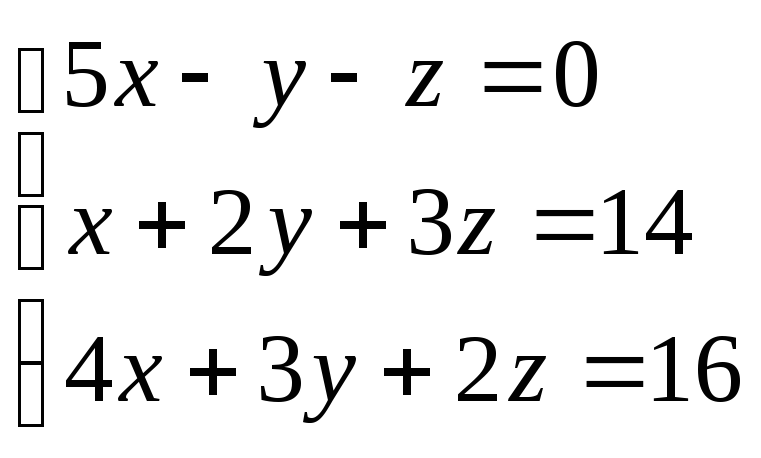
х=,B=,A=

Знайдемо обернену матрицю А^–1.

 = det A=5(4–9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = – 30.

А₁₁== – 5;А₂₁= –= – 1;А₃₁== –1;

А₁₂= –А₂₂=А₃₂= –

А₁₃=А₂₃= –А₃₃=

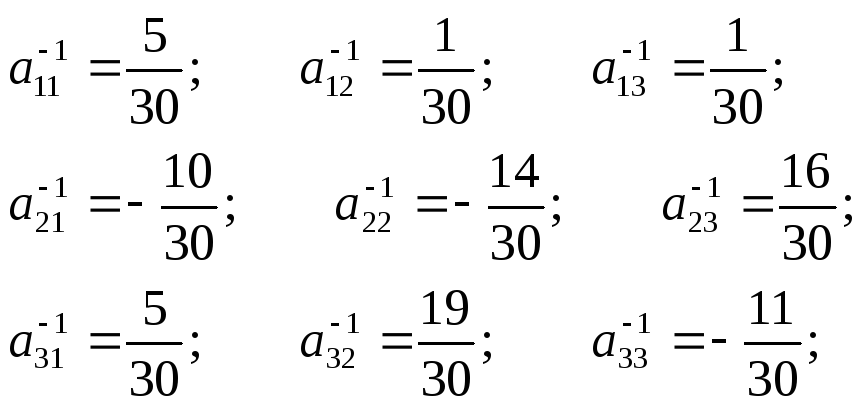A^–1=;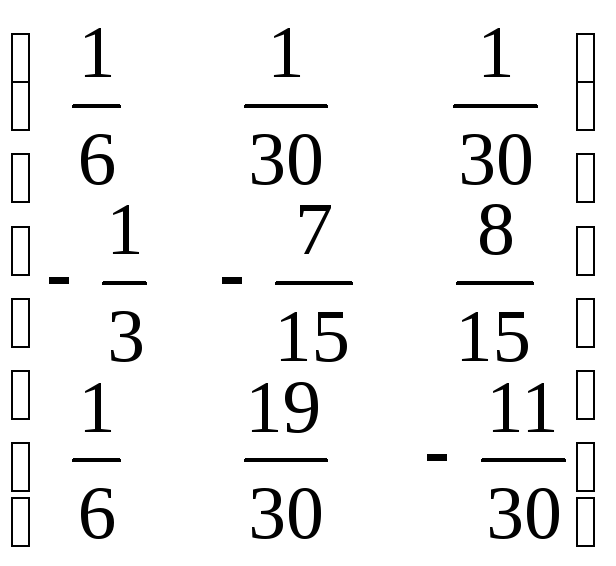

Зробимо перевірку:

AA^–1=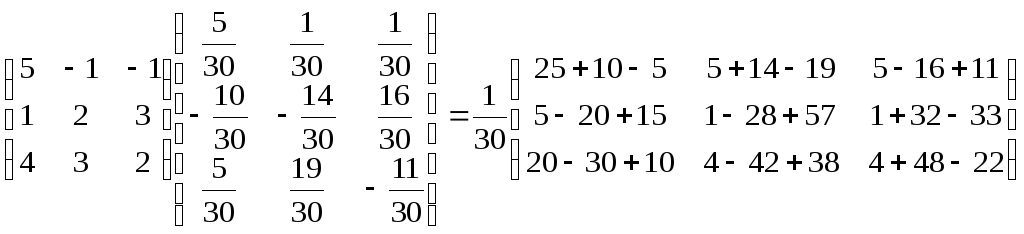=E.

Знаходимо матрицю х.

х==А^–1В= =.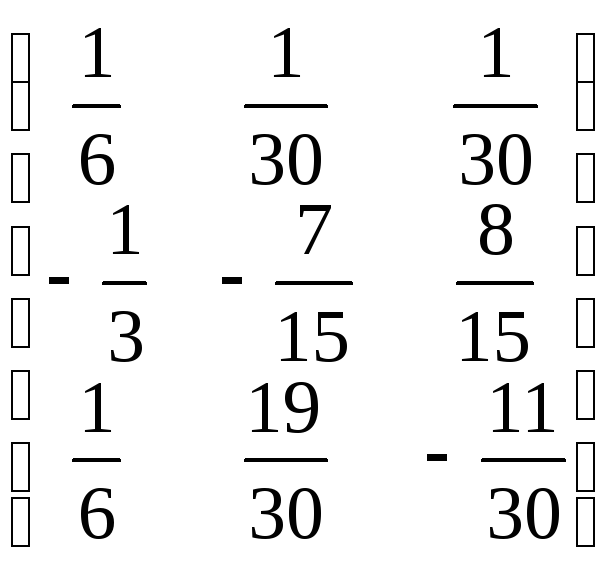

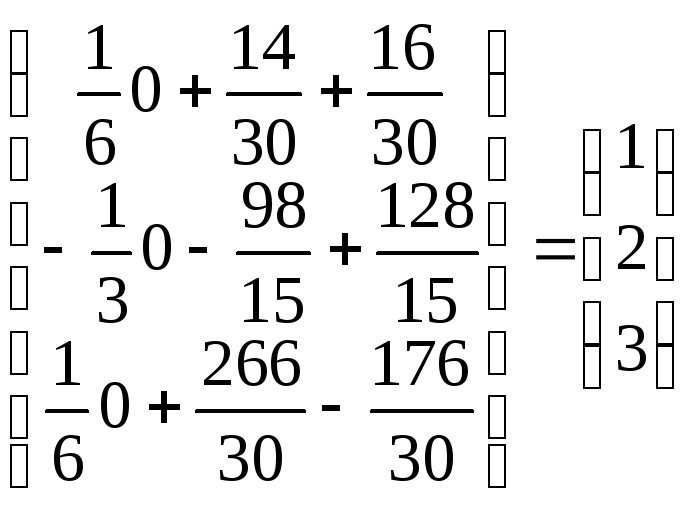Отже розв’язок системи: x=1;y= 2;z= 3.

Незважаючи на обмеження можливості застосування даного методу й складність обчислень при більших значеннях коефіцієнтів, а також систем високого порядку, метод може бути легко реалізований на ЕОМ.