Число е.

Розглянемо послідовність {x_n} =.

Якщо послідовність {x_n} монотонна й обмежена, то вона має скінченну границю.

За формулою бінома Ньютона:

або, що те ж саме

Покажемо, що послідовність {x_n} – зростаюча. Дійсно, запишемо виразx_n+1і прирівняємо його з виразомx_n:

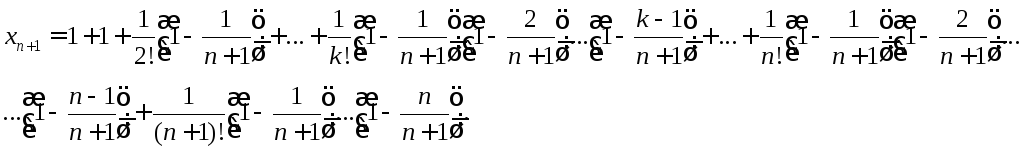
Кожний доданок у виразі x_n+1більше відповідного значенняx_n, і, крім того, вx_n+1додається ще один позитивний доданок. Таким чином, послідовність {x_n} зростаюча.

Доведемо тепер, що при будь-якому n її члени не перевершують трьох: x_n< 3.

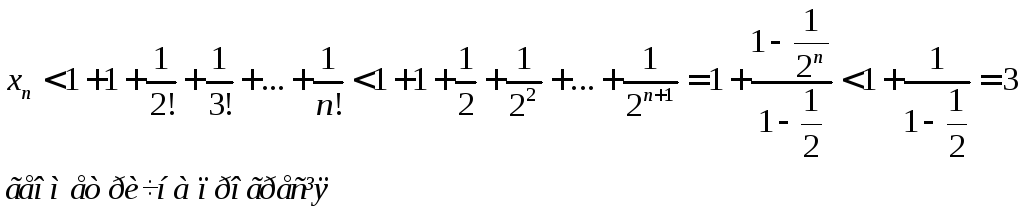
Отже, послідовність 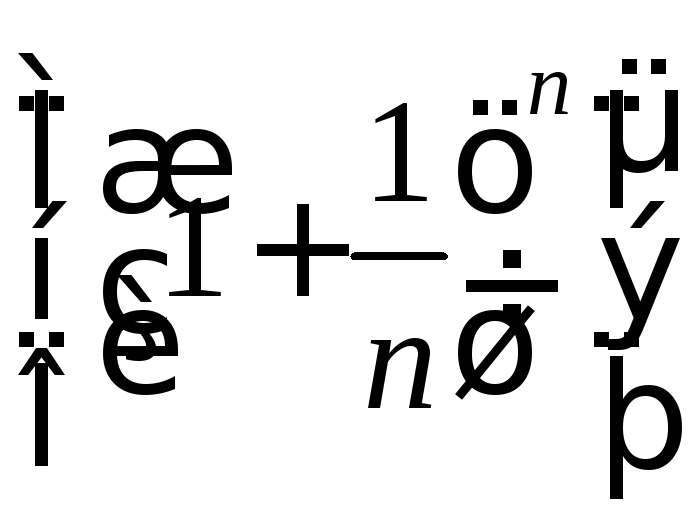– монотонно зростаюча і обмежена зверху, тобто має скінченну границю. Цю границю прийнято позначати буквоюе.

З нерівності треба, щоб. Відкидаючи в рівності для {x_n} всі члени, починаючи із четвертого, маємо:

переходячи до границі, одержуємо

Таким чином, число е розміщене між числами 2,5 і 3. Якщо взяти більшу кількість членів послідовності, то можна одержати більш точну оцінку значення числа е.

Можна показати, що число еірраціональне і його значення дорівнює 2,71828...

Аналогічно можна показати, що , розширивши вимоги дохдо будь-якого дійсного числа:

Припустимо:

Знайдемо

Число еє основою натурального логарифма.

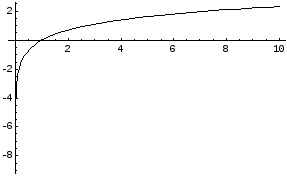
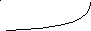
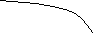
Вище представлений графік функції y= lnx.

Зв'язок натурального й десяткового логарифмів.

Нехай х= 10^у, тоді ln x= ln10^y, отже ln x=yln10.

, де М = 1/ln100,43429… – модуль переходу.

Границя функції в точці.

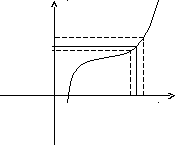yf(x)

A+

A

A–

0 a–aa+x

Нехай функція f(x) визначена в деякому околі точких=а(тобто в самій точціх=афункція може бути й невизначена).

Визначення.ЧислоАназиваєтьсяграницеюфункціїf(x) приха, якщо для кожного>0 існує таке число>0, що для всіххтаких, що

вірна нерівність .

Те ж визначення може бути записане в іншому вигляді:

Якщо а–<x<a+,xa, то вірна нерівністьА–<f(x) <A+.

Запис границі функції в точці:

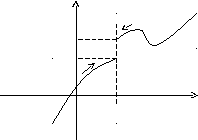
Визначення.Якщоf(x)A₁прихатільки приx<a, то- називаєтьсяграницеюфункціїf(x) в точціх=аліворуч, а якщоf(x)A₂прихатільки приx>a, тоназиваєтьсяграницеюфункціїf(x) в точціх=аправоруч.

у

f(x)

А₂

А₁

0 ax

Наведене вище визначення відповідає випадку, коли функція f(x) не визначена в самій точціх=а, але визначена в деякій як завгодно малому околі цієї точки.

Межі А₁іА₂називаються такожоднобічними границямифункціїf(x) у точціх=а. Також кажуть, щоА–скінченна границяфункціїf(x).

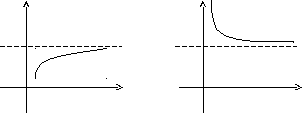
Границя функції при прямуванні аргументу до нескінченності.

Визначення.ЧислоАназиваєтьсяграницеюфункціїf(x) прих, якщо для будь-якого числа>0 існує таке числоМ>0, що для всіхх,х>Mвиконується нерівність

При цьому вважається, що функція f(x) визначена в околиці нескінченності.

Записують:

Графічно можна представити:

yy

AA

0 0

xx

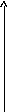
yy

AA

0 0

xx

Аналогічно можна визначити границі для будь-якогох>Mі

для будь-якогох<M.

Основні теореми про границі.

Теорема 1., деС= const.

Наступні теореми справедливі в припущенні, що функції f(x) іg(x) мають скінченні границі при .

Теорема 2.

Доведення цієї теореми буде наведено нижче.

Теорема 3.

Наслідок.

Теорема 4.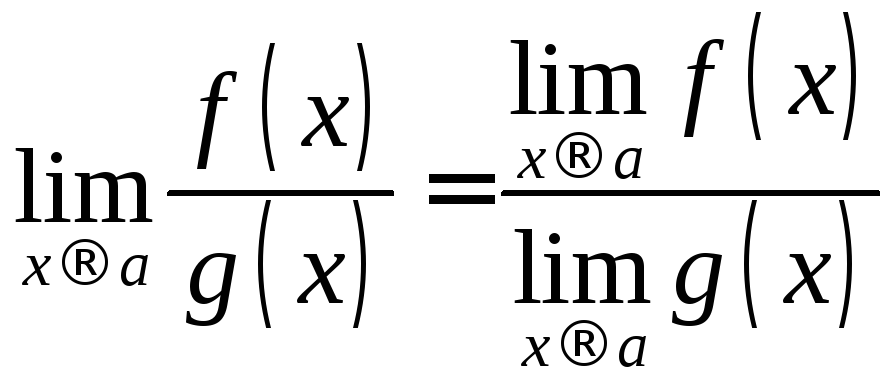за умови

Теорема 5.Якщо f(x)>0 поблизу точки х = а й , то А>0.

Аналогічно визначається знак границі при

Теорема 6.Якщо поблизу точки х = а й, то й.

Визначення.Функціяf(x) називаєтьсяобмеженою поблизу точких=а, якщо існує таке числоМ>0, щоf(x)<Mпоблизу точких=а.

Теорема 7.Якщо функція f(x) має скінченну границю при , то вона обмежена поблизу точки х = а.

Доведення.Нехай, тобто, тоді

або

, тобто

деМ=+А

Теорему доведено.