Елементарні перетворення матриці.
Визначення.Елементарними перетвореннямиматриці назвемо наступні перетворення:
1) множення рядка на число, відмінне від нуля;
2) додавання до елементів одного рядка елементів іншого рядка;
3) перестановка рядків;
4) викреслювання (видалення) одного з однакових рядків (стовпців);
5) транспонування;
Ті ж операції, застосовані до стовпців, також називаються елементарними перетвореннями.
За допомогою елементарних перетворень можна до якого-небудь рядка або стовпця додати лінійну комбінацію інших рядків ( стовпців ).
Мінори.
Вище було використане поняття додаткового мінораматриці. Дамо визначення мінора матриці.
Визначення.Якщо в матриціАвидалити кілька довільних рядків і стільки ж довільних стовпців, то матриця, складена з елементів, розташованих на перетині цих рядків і стовпців називаєтьсямінором матриціА. Якщо виділеноsрядків і стовпців, то отриманий мінор називається мінором порядкуs.
Відмітимо, що вищесказане застосовне не тільки до квадратних матриць, але й до прямокутних.
Якщо викреслити з вихідної квадратноїматриціАвиділені рядки й стовпці, то отримана матриця буде додатковим мінором.
Алгебраїчні доповнення.
Визначення.Алгебраїчним доповненняммінора матриці називається визначник йогододаткового мінора, помножений на (–1) у степені, рівному сумі номера рядка і номера стовпця мінора матриці.
В окремому випадку, алгебраїчним доповненням елемента матриці називається його додатковий мінор, узятий зі своїм знаком, якщо сума номерів стовпця й рядка, на яких стоїть елемент, є число парне і з протилежним знаком, якщо непарне.
Теорема Лапласа.Якщо обрано s рядків матриці з номерами i1, … ,is, то визначник цієї матриці дорівнює сумі добутків всіх елементів, розташованих в обраних рядках на їхні алгебраїчні доповнення.
Обернена матриця.
Визначимо операцію ділення матриць як операцію, обернену множенню.
Визначення. Якщо існують квадратні матриціХиАодного порядку, що задовольняють умові:
XA = AX = E,
де Е- одинична матриця того ж самого порядку, що й матрицяА, те матрицяХназиваєтьсяоберненою до матриціАи позначаєтьсяА–1.
Кожна квадратна матриця з визначником, не рівним нулю має обернену матрицю й притім тільки одну.
Розглянемо загальний підхід до знаходження оберненої матриці. Виходячи з визначення добутку матриць, можна записати:
AX = E
,i=( 1,n ),j=( 1,n),
eij = 0,ij,
eij = 1,i=j.
Таким чином, одержуємо систему рівнянь:
,
Вирішивши цю систему, знаходимо елементи матриці Х.
Приклад.Дано матрицюА=
,
знайтиА–1.
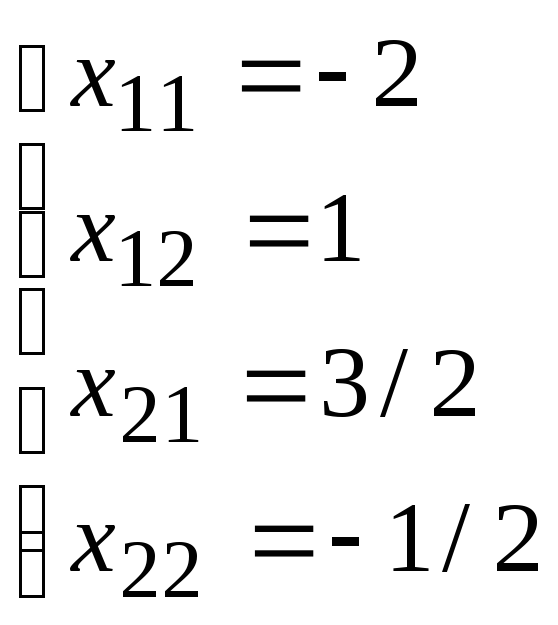
Таким чином,
А–1=
.
Однак, такий спосіб незручний при знаходженні обернених матриць більших порядків, тому звичайно застосовують наступну формулу:
,
де Aji– алгебраїчне доповнення елементааjiматриці А.
Приклад.Дано матрицюА=
,
знайтиА–1.
det A= 4 – 6 = – 2.
M11=4;M12= 3; M21= 2;M22=1
x11= – 2;x12= 1;x21= 3/2;x22= – 1/2
Таким чином,
А–1=
.
Властивості обернених матриць.
Вкажемо наступні властивості обернених матриць:
1) (A–1)–1=A;
2) (AB)–1=B–1A–1
3) (AT)–1= (A–1)T.
Приклад.Дано матрицюА=
,
знайтиА3.
А2=АА=
=
;A3=
=
.
Відзначимо, що матриці
і
є комутуючими.
Приклад.Обчислити визначник
.
= – 1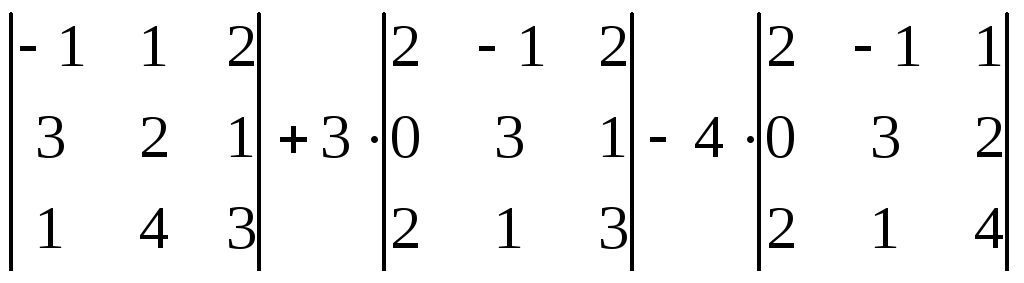
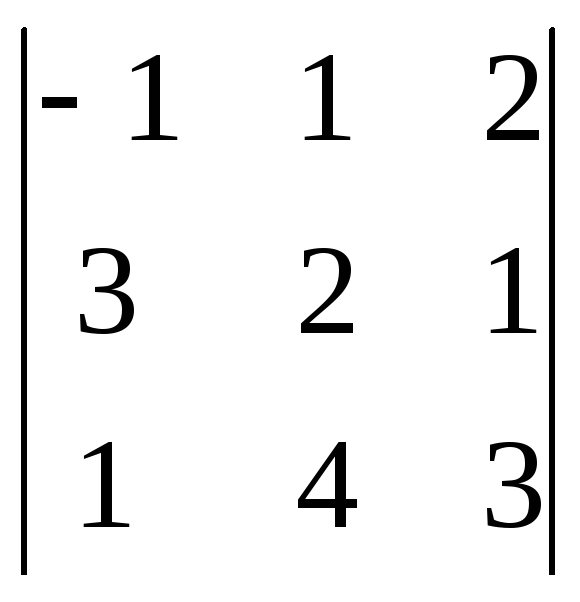= – 1(6 – 4) – 1(9 – 1) + 2(12 – 2) = – 2 – 8 + 20 =
10.
=
=
2(0 – 2) – 1(0 – 6) = 2.
=
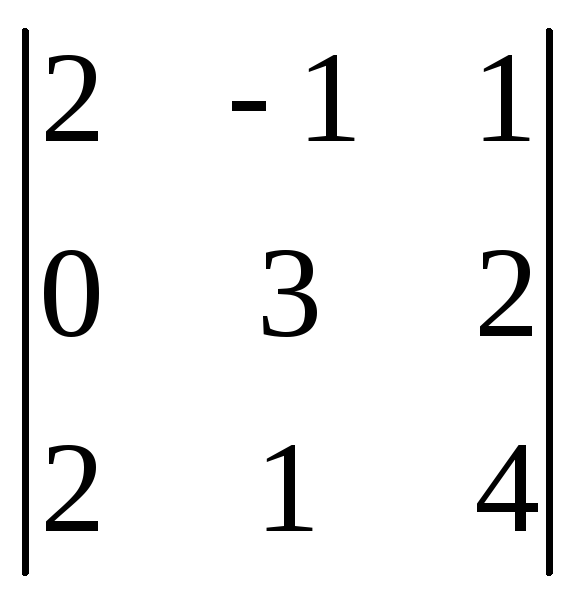= 2(–4) – 3(–6) = –8 + 18 = 10.
Значення визначника: – 10 + 6 – 40 = – 44.