Лекція №3.

Тема: Теорія деформацій.

1. Складові переміщення, деформацій. Геометричні співвідношення Коші.

2. Рівняння неперервності деформацій.

3. Узагальнений закон Гука.

3.1. Складові переміщення, деформацій. Геометричні співвідношення Коші.

Дослідимо деформацію пружного тіла. Для її визначення порівняємо положення точок тіла до та після прикладання навантаження. На рис. 10 показано тіло та точка А з координатами x, y, z. Під дією навантаження точка А переміститься в нове положення А' з координатами x', y', z'. Вектор АА' носить назву – вектор переміщення точки А.

Розрізняють два види переміщень: переміщення всього тіла як єдиного цілого без його деформації та переміщення, пов’язане з деформуванням тіла. Переміщення першого виду вивчають в теоретичній механіці як переміщення абсолютно твердого тіла. В теорії пружності розглядають тільки переміщення, пов’язані з деформуванням тіла.

Будемо вважати, що розглядуване тіло закріплено таким чином, що воно не може переміщуватися, як абсолютно тверде тіло. Позначимо проекції вектора переміщення точки А на координатні осі через u, w, z. Вони дорівнюють різниці відповідних координат точок А та А':

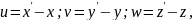
та є функціями координат:

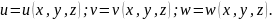
Різниця в переміщеннях окремих точок тіла викликає його деформування. Розглянемо нескінченно малий паралелепіпед з ребрами dx, dy, dz, який вирізали з пружного тіла навколо довільної точки А. Внаслідок різних переміщень його точок паралелепіпед деформується таким чином, що змінюється довжина його ребер та видозмінюються попередньо прямі кути між гранями.

Н а рис. 3.2 зображено два ребра цього паралелепіпеду: ребро АВ, паралельне осі х, та ребро АС, паралельне осі y. Довжина ребра АВ дорівнює dx, ребра АС – dz. Після деформації точки А, В, С займуть нові положення: А', В', С'. При цьому точка А отримає переміщення, складові якого в площині креслення дорівнюють u та v. Точка В, яка знаходиться на нескінченно малій відстані dx від точки А, отримає переміщення, складові якого будуть відрізнятися від складових переміщення точки А на нескінченно малу величину за рахунок зміни координати х:

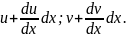
Складові переміщення точки С будуть відрізнятися від складових переміщення точки А на нескінченно малу величину за рахунок зміни координати y:

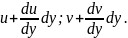
Довжина проекції ребра АВ на вісь х після деформації:

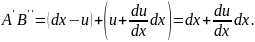(3.1)

Проекція абсолютної деформації ребра АВ на вісь х:

(3.2)

Відносна деформація вздовж осі х:

. (3.3)

Вираз (3.3) називають лінійною деформацією за напрямком осі х.

Аналогічно можна отримати лінійну деформацію за напрямком координатних осей y та z:

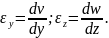(3.4)

Отже, лінійна деформація в будь-якому напрямку дорівнює частній похідній складової переміщення в цьому напрямку за змінною в цьому ж напрямку.

Розглянемо зміни кутів між ребрами паралелепіпеду (рис. 3.2). Тангенс кута повороту ребра АВ в площині xOy:

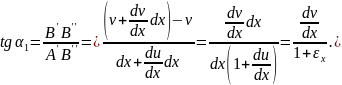(3.5)

Обмежуючись розглядом тільки малих деформацій, можна прийняти tgα₁ ≈ α₁ та нехтуючи лінійною деформацією ε_х, як нескінченно малою у порівнянні з одиницею, отримаємо:

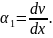(3.6)

Аналогічно можна визначити кут повороту ребра АС в цій же площині:

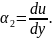(3.7)

Кут зсуву в площині xOy, тобто зміну попередньо прямого кута ВАС, називають кутовою деформацією та визначають як суму кутів повороту ребер АВ та АС:

(3.8)

Аналогічно знаходять кутові деформації в двох інших координатних площинах:

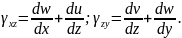(3.9)

Кутова деформація в будь-якій площині дорівнює сумі частних похідних складових переміщення в цій площині по переміщенню в перпендикулярних напрямках.

Формули (3.3), (3.4), (3.8), (3.9) дають шість основних залежностей складових лінійних та кутових деформацій від складових переміщення:

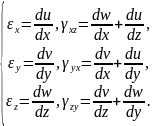(3.10)

Останні залежності називають геометричними співвідношеннями Коші.

Переходячи до межі, коли ребра паралелепіпеду прямують до нуля, формули (3.10) визначають лінійні та кутові деформації біля точки А.

Правило знаків для складових деформації:

• додатнім лінійним деформаціям відповідає подовження за відповідними напрямками, а від’ємним – скорочення;

• додатнім кутовим деформаціям відповідає зменшення кутів між додатнім напрямком координатних осей, а від’ємним – збільшення цих же кутів.

У випадку, коли потрібно знайти об’ємну деформацію, розглядають нескінченно малий паралелепіпед об’ємом dV = dxdydz. Вважають, що зміна цього об’єму пов’язана тільки зі зміно довжини ребер, а кутовими деформаціями нехтують, як більшого порядку малості.

Довжина ребра АВ, яка попередньо дорівнювала dx, після деформування відповідно до (3.1) дорівнює:

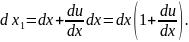
Скориставшись першим рівнянням (3.10), отримаємо:

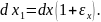(3.11)

Аналогічно отримують довжини інших ребер після деформації:

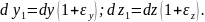(3.12)

Об’єм паралелепіпеду після деформації дорівнює:

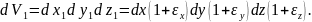
Розкривши дужки, отримаємо:

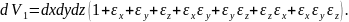
Нехтуючи в дужках величинами другого та третього порядків малості та враховуючи, що dxdydz = dV, знайдемо:

Позначимо відносну зміну об’єму 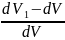через θ та отримаємо:

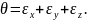(3.13)

Таким чином, об’ємна деформація дорівнює сумі лінійних деформацій за трьома перпендикулярними напрямками.

Використовуючи рівняння (3.10) об’ємну деформацію можна виразити через складові переміщення:

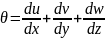. (3.14)