“Курс вищої математики. Частина 1.”

Зміст КВМ Частина 1.

КУРС

ВИЩОЇ

МАТЕМАТИКИ

Короткий конспект лекцій

Частина 1

2005

Комплексні числа.

Визначення.Комплексним числом z називається вираз, деa іb– дійсні числа,i– уявна одиниця, що визначається співвідношенням:

При цьому число aназиваєтьсядійсною частиноючислаz(a = Re z), аb-уявною частиною(b = Im z).

Якщо a =Re z =0, то числоzбуде чисто уявним, якщоb = Im z = 0, то числоzбуде дійсним.

Визначення.Числайназиваютьсякомплексно спряженими.

Визначення.Два комплексних числайназиваються рівними, якщо відповідно рівні їх дійсні й уявні частини:

Визначення.Комплексне число дорівнює нулю, якщо відповідно дорівнюють нулю дійсна й уявна частини.

Поняття комплексного числа має геометричне тлумачення. Множина комплексних чисел є розширенням множини дійсних чисел за рахунок включення множини уявних чисел. Комплексні числа містять у собі всі множини чисел, які вивчалися раніше. Так натуральні, цілі, раціональні, ірраціональні, дійсні числа є, загалом кажучи, окремими випадками комплексних чисел.

Якщо будь-яке дійсне число може бути геометрично представлене у вигляді точки на числовій прямій, то комплексне число представляється точкою на площині, координатами якої будуть відповідно дійсна й уявна частини комплексного числа. При цьому горизонтальна вісь буде дійсною числовою віссю, а вертикальна – уявною віссю.

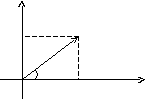
у

A(a,b)

rb



Оax

Таким чином, на осі Охрозташовуються дійсні числа, а на осіОу– чисто уявні.

За допомогою подібного геометричного подання можна представляти числа в так званій тригонометричній формі.

Тригонометрична форма комплексного числа.

З геометричних міркувань видно, що . Тоді комплексне число можна представити у вигляді:

Така форма запису називається тригонометричною формою запису комплексного числа.

При цьому величина rназиваєтьсямодулем комплексного числа, а кут нахилу– аргументом комплексного числа.

.

З геометричних міркувань видно:

Очевидно, що комплексно спряжені числа мають однакові модулі й протилежні аргументи.

Дії з комплексними числами.

Основні дії з комплексними числами випливають із дій з багаточленами.

1) Додавання й віднімання.

2) Множення.

У тригонометричній формі:

,

З випадку комплексно - сполучених чисел:

3) Ділення.

Утригонометричній формі:

4) Піднесення до степеня.

З операції множення комплексних чисел треба, що

У загальному випадку одержимо:

,

де n –ціле додатне число.

Цей вираз називаєтьсяформулою Муавра. (Абрахам де Муавр (1667–1754) – англійський математик)

Формулу Муавра можна використати для знаходження тригонометричних функцій подвійного, потрійного й т.д. кутів.

Приклад.Знайти формулиі.

Розглянемо деяке комплексне число

Тоді з однієї сторони .

По формулі Муавра:

Дорівнюючи, одержимо

Оскільки два комплексних числа рівні, якщо рівні їх дійсні й уявні частини, то

Одержали відомі формули подвійного кута.

5) Добування кореня з комплексного числа.

Підносячи до степеня, одержимо:

Звідси:

Таким чином, корінь n-го степеня з комплексного числа маєnрізних значень.

Показникова форма комплексного числа.

Розглянемо показову функцію

Можна показати, що функція wможе бути записана у вигляді:

Дана рівність називаєтьсярівнянням Ейлера. Висновок цього рівняння буде розглянутий пізніше.

Для комплексних чисел будуть справедливі наступні властивості:

1)

2)

3) деm– ціле число.

Якщо в рівнянні Ейлера показник степеня прийняти за чисто уявне число (х=0), то одержуємо:

Для комплексно спряженого числа одержуємо:

З цих двох рівнянь одержуємо:

Цими формулами користуються для знаходження значень ступенів тригонометричних функцій через функції кратних кутів.

Якщо представити комплексне число в тригонометричній формі:

і скористаємося формулою Ейлера:

Отримана рівність і є показниковою формою комплексного числа.