Розклад багаточлена на множники.

Визначення.Функція виглядуf(x)називаєтьсяцілою раціональноюфункцією відх.

Теорема Безу.(Етьєн Безу (1730–1783) – французький математик)

При діленні багаточлена f(x) на різницю x – a виходить остача, рівна f(a).

Доведення.При діленні багаточленаf(x) на різницюx – a часткою буде багаточленf₁(x) степеня на одиницю меншого, ніжf(x), а остачею – стале числоR.

Переходячи до границі при х  a, одержуємоf(a) = R.

Наслідок.Якщо, а – корінь багаточлена, тобто f(a) = 0, то багаточлен f(x) ділиться на (х – а) без остачі.

Визначення.Якщо рівняння має виглядР(х) = 0, деР(х) – багаточлен степеняn, то це рівняння називаєтьсяалгебраїчнимрівнянням ступеняn.

Теорема.(Основна теорема алгебри)Усяка ціла раціональна функція f(x) має, принаймні, один корінь, дійсний або комплексний.

Теорема.Усякий багаточлен n-го степеня розкладається на n лінійних множників вигляду (x – a) і множник, що дорівнює коефіцієнту при xⁿ.

Теорема.Якщо два багаточлени тотожно рівні один одному, то коефіцієнти одного багаточлена дорівнюють відповідним коефіцієнтам іншого.

Якщо серед коренів багаточлена зустрічаються кратні коріння, то розклад на множники має вигляд:

k_i– кратність відповідного кореня.

Звідси випливає, що будь-який багаточлен n-го степеня має рівно n коренів (дійсних або комплексних).

Ця властивість має велике значення для розв’язання алгебраїчних рівнянь, диференціальних рівнянь і відіграє важливу роль в аналізі функцій.

Розгляньмо кілька прикладів дій з комплексними числами.

Приклад.Дано два комплексних числа. Потрібно а) знайти значення виразув алгебраїчній формі, б) для числазнайти тригонометричну форму, знайтиz²⁰, знайти корінь рівняння

1. Очевидно, справедливе наступне перетворення:

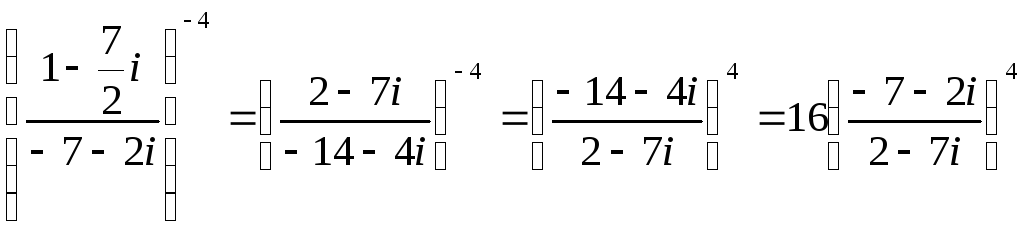
Далі виконуємо ділення двох комплексних чисел:

Одержуємо значення заданого виразу: 16(–i)⁴ = 16i⁴=16.

б) Число представимо у вигляді, де

Тоді .

Для знаходження скористаємося формулою Муавра.

Якщо , то

Лінійна алгебра. Основні визначення.

Визначення.Матрицеюрозміруmn, деm– число рядків,n– число стовпців, називається таблиця чисел, розташованих у певному порядку. Ці числа називаються елементами матриці. Місце кожного елемента однозначно визначається номером рядка й стовпця, на перетині яких він перебуває. Елементи матриці позначаютьсяa_ij, деi –номер рядка, аj– номер стовпця.

А=

Основні дії над матрицями.

Матриця може складатися як з одного рядка, так і з одного стовпця. Загалом кажучи, матриця може складатися навіть із одного елемента.

Визначення.Якщо число стовпців матриці дорівнює числу рядків (m=n), то матриця називаєтьсяквадратною.

Визначення.Матриця вигляду:

=E,

називаєтьсяодиничною матрицею.

Визначення.Якщоa_mn = a_nm , то матриця називаєтьсясиметричною.

Приклад.– симетрична матриця

Визначення. Квадратна матриця видуназиваєтьсядіагональною матрицею.

Додавання й відніманняматриць зводиться до відповідних операцій над їхніми елементами. Найголовнішою властивістю цих операцій є те, що вонивизначені тільки для матриць однакового розміру. Таким чином, можливо визначити операції додавання й віднімання матриць:

Визначення. Сумою (різницею) матриць є матриця, елементами якої є відповідно сума (різниця) елементів вихідних матриць.

c_ij = a_ij  b_ij

C = А + В = В + А.

Операція множення (ділення)матриці будь-якого розміру на довільне число зводиться до множення (ділення) кожного елемента матриці на це число.

 (А В) =А В

А() =АА

Приклад.Дано матриціА=;B=, знайти 2А+В.

2А=, 2А+В=.