Теорема Кронекера-Капеллі.

(умова сумісності системи)

(Леопольд Кронекер (1823-1891) німецький математик)

Теорема: Система сумісна (має хоча б один розв’язок) тоді й тільки тоді, коли ранг матриці системи дорівнює рангу розширеної матриці.

Rank А= RankА^*.

Очевидно, що система (1) може бути записана у вигляді:

x₁+x₂+ … +x_n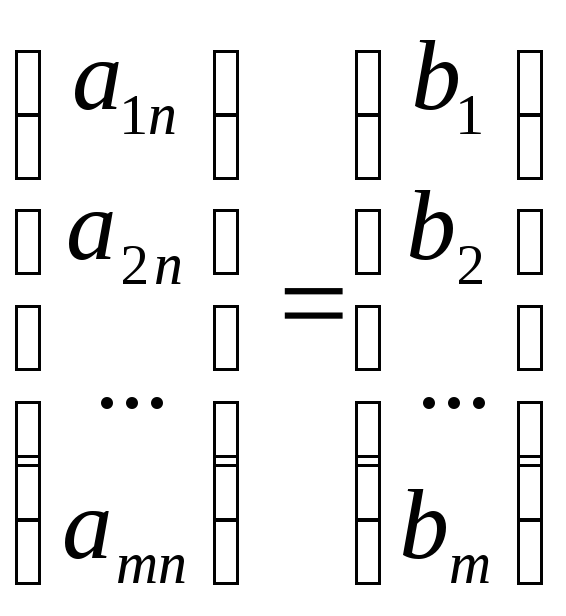

Доведення.

1) Якщо розв’язок існує, то стовпець вільних членів є лінійною комбінацією стовпців матриці А, а значить додавання цього стовпця в матрицю, тобто перехідАА^*не змінює рангу.

2) Якщо Rank А= RankА^*, те це означає, що вони мають той самийбазовий мінор. Стовпець вільних членів – лінійна комбінація стовпців базового мінору, тоді вірний запис, наведений вище.

Приклад.Перевіритисумісністьлінійних рівнянь:

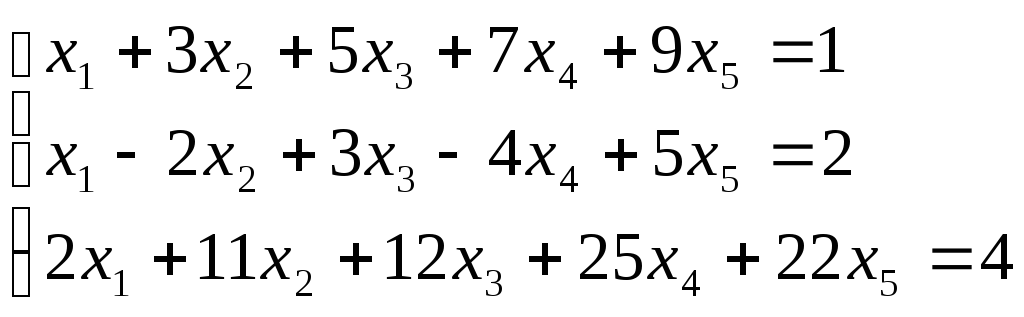
A=

~ .RankA= 2.

A* =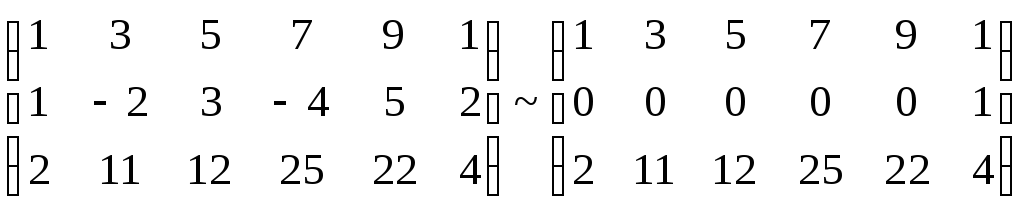RankA* = 3.

Система несумісна.

Приклад.Перевіритисумісністьлінійних рівнянь.

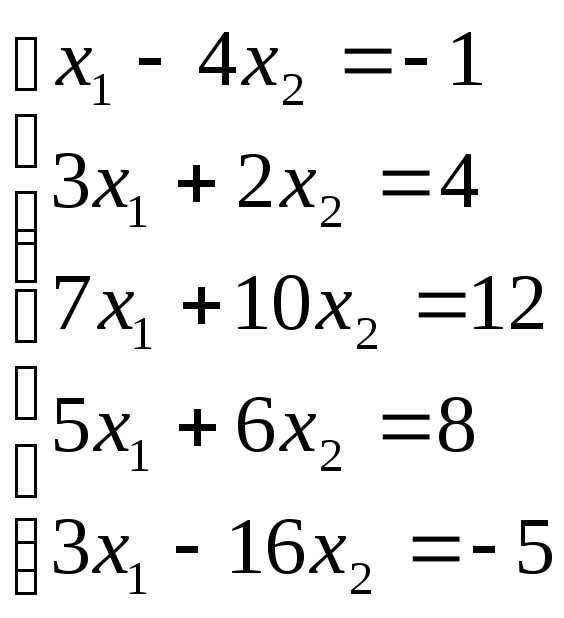А=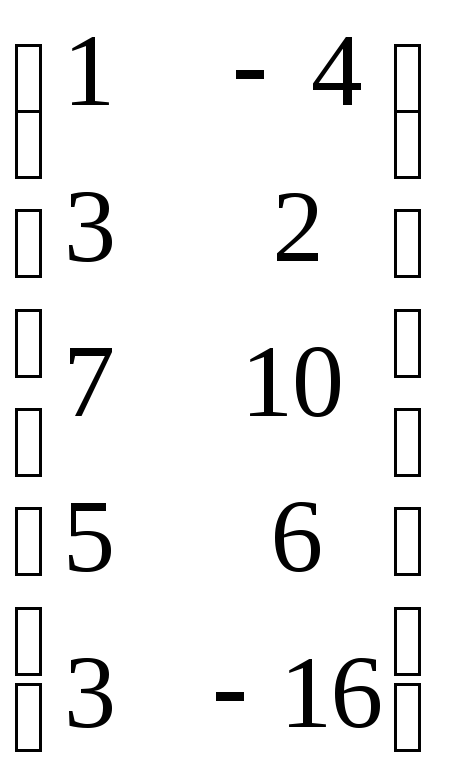;= 2 + 12 = 140; RankА= 2;

A* =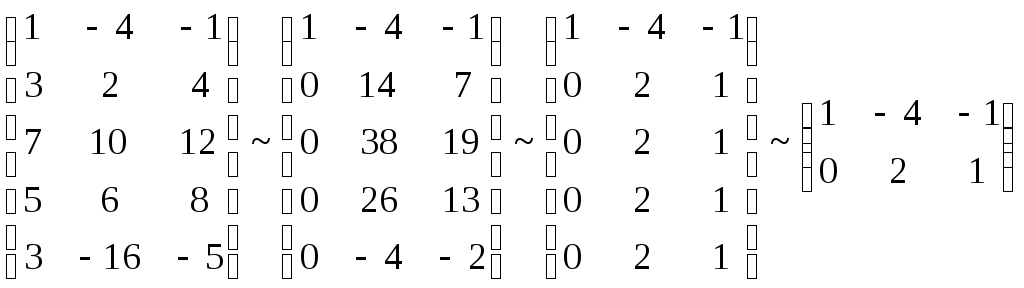

RankA* = 2.

Система сумісна. Розв’язок: x₁= 1;x₂=1/2.

Метод Гауса.

(Карл Фрідріх Гаус (1777-1855) німецький математик)

На відміну від матричного методуіметода Крамера, метод Гауса може бути застосований до систем лінійних рівнянь із довільним числом рівнянь і невідомих. Суть методу полягає в послідовному виключенні невідомих.

Розглянемо систему лінійних рівнянь:

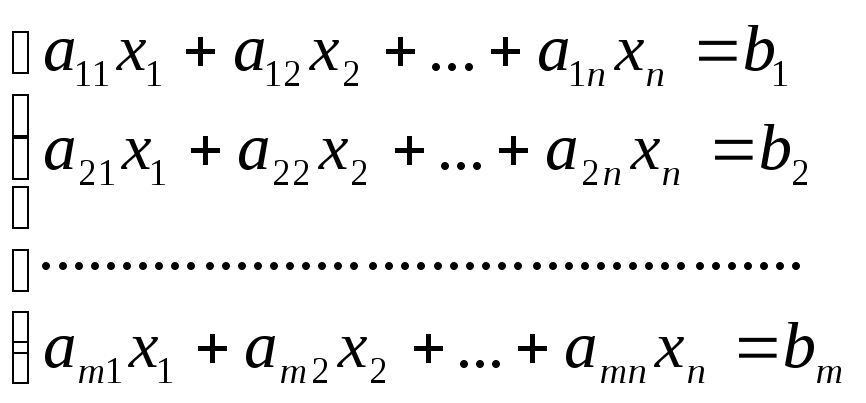
Розділимо обидві частини 1-го рівняння на a₁₁0, потім:

1) помножимо на а₂₁і віднімемо із другого рівняння

2) помножимо на а₃₁і віднімемо із третього рівняння

і т.д.

Одержимо:

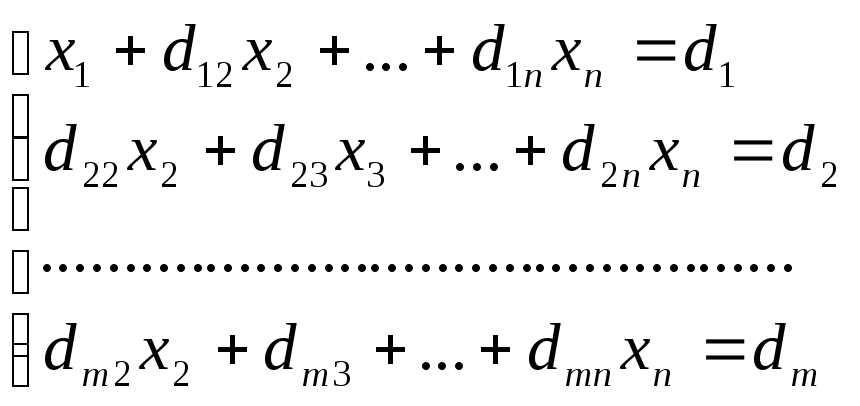, деd_1j = a_1j/a₁₁, j = 2, 3, …, n+1...

d_ij = a_ij – a_i1d_1j i = 2, 3, … , n; j = 2, 3, … , n+1...

Далі повторюємо цієї ж дії для другого рівняння системи, потім - для третього й т.д.

Приклад.Вирішити систему лінійних рівнянь методом Гауса.

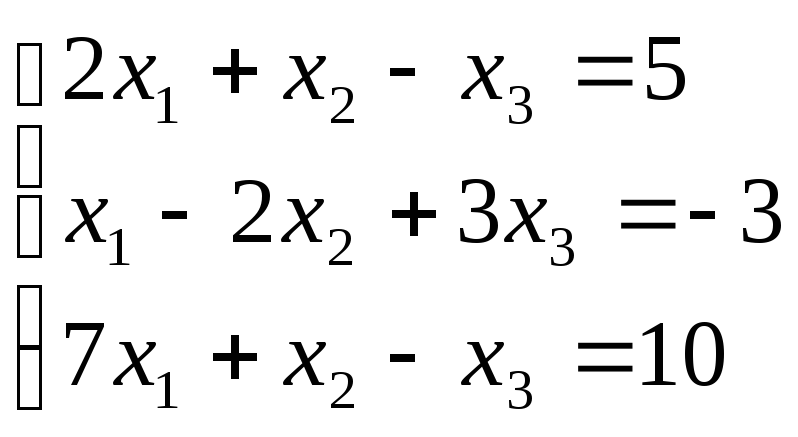
Складемо розширену матрицю системи.

А* =

Таким чином, вихідна система може бути представлена у вигляді:

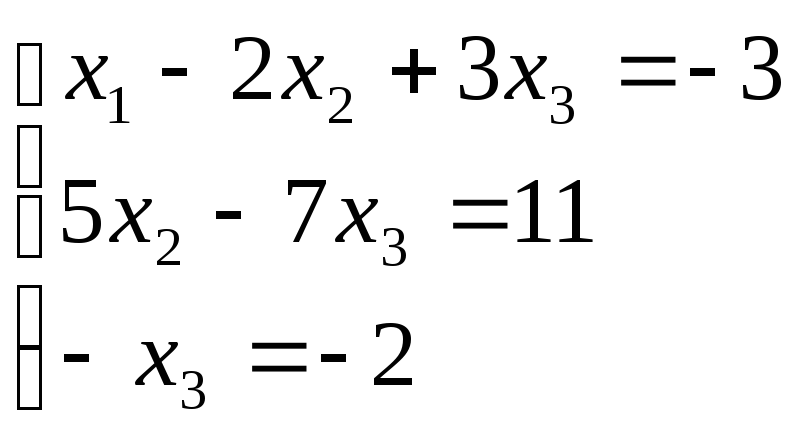, звідки одержуємо:x₃= 2;x₂= 5;x₁= 1.

Приклад.Вирішити систему методом Гауса.

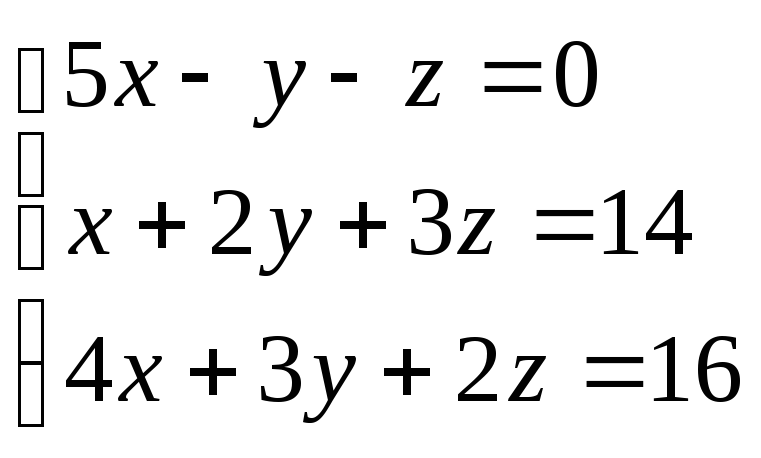
Складемо розширену матрицю системи.

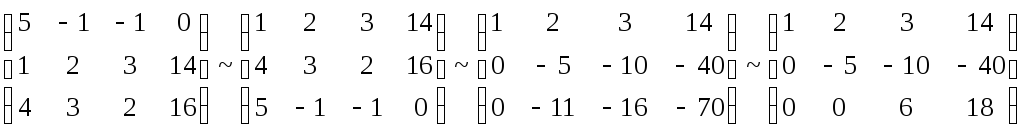
Таким чином, вихідна система може бути представлена у вигляді:

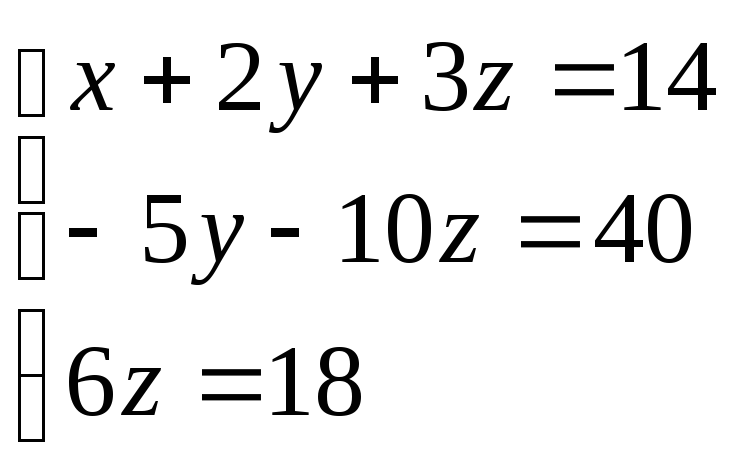, звідки одержуємо:z= 3;y= 2;x= 1.

Отримана відповідь збігається з відповіддю, отриманою для даної системи методом Крамера й матричним методом.

Для самостійного розв’язання:

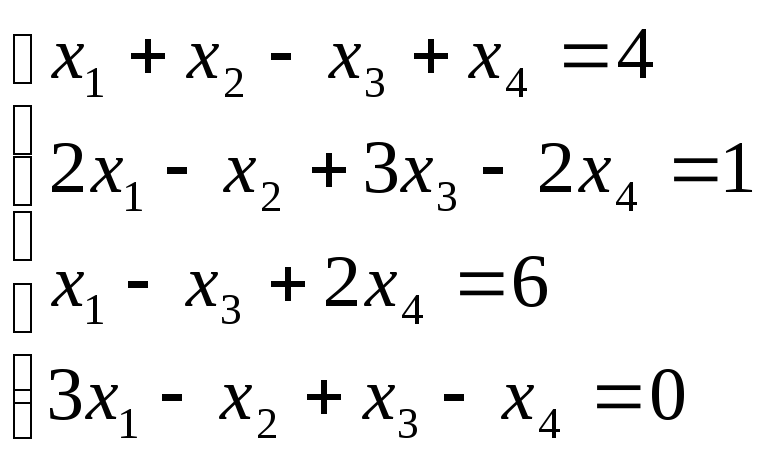Відповідь: {1, 2, 3, 4}.

Елементи векторної алгебри.

Визначення.Векторомназивається прямолінійний відрізок (упорядкована пара точок). До векторів належить також інульовийвектор, початок і кінець якого збігаються.

Визначення.Довжиною (модулем)вектора називається відстань між початком і кінцем вектора.

Визначення.Вектори називаються колінеарними, якщо вони розташовані на одній або паралельних прямих. Нульовий вектор колінеарний до будь-якого вектора.

Визначення.Вектори називаютьсякомпланарними, якщо існує площина, який вони паралельні.

Колінеарні вектори завжди компланарні, але не всі компланарні вектори колінеарні.

Визначення.Вектори називаютьсярівними, якщо вони колінеарні, однаково спрямовані й мають однакові модулі.

Усякі вектори можна привести до спільного початку, тобто побудувати вектори, відповідно рівні даним, що мають загальний початок. З визначення рівності векторів треба, що будь-який вектор має нескінченно багато векторів, рівних йому.

Визначення.Лінійними операціяминад векторами називається додавання й множення на число.

Сумою векторів є вектор –

Добуток – , при цьомуколінеарний до.

Вектор співнаправлений з вектором(), якщо> 0.

Вектор протилежно спрямований до вектора(  ), якщо< 0.