Квадратичні форми.

Визначення:Однорідний багаточлен другого ступеня щодо зміннихх₁ іх₂

Ф(х₁, х₂) = а₁₁

не утримуючого вільного члена й невідомих у першому ступені називається квадратичною формоюзміннихх₁іх₂.

Визначення:Однорідний багаточлен другого ступеня щодо зміннихх₁,х₂іх₃

не утримуючого вільного члена й невідомих у першому ступені називається квадратичною формоюзміннихх₁,х₂іх₃.

Розглянемо квадратичну форму двох змінних. Квадратична форма має симетричну матрицюА=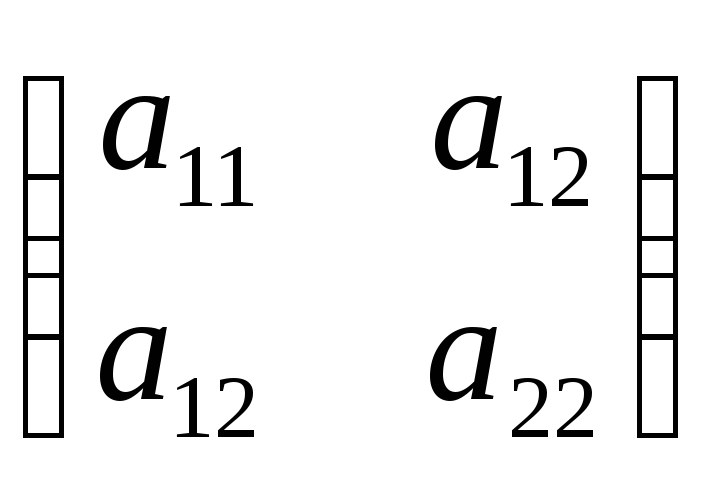. Визначник цієї матриці називаєтьсявизначником квадратичної форми.

Нехай на площині заданий ортогональний базис . Кожна точка площини має в цьому базисі координатих₁,х₂.

Якщо задано квадратичну форму Ф(х₁, х₂) = а₁₁, то її можна розглядати як функцію від зміннихх₁іх₂.

Приведення квадратичних форм до канонічного вигляду.

Розглянемо деяке лінійне перетворення Ас матрицею.

Це симетричне перетворення можна записати у вигляді:

y₁=a₁₁x₁+a₁₂x₂

y₂=a₁₂x₁+a₂₂x₂

де у₁іу₂– координати векторав базисі.

Очевидно, що квадратична форма може бути записана у вигляді

Ф(х₁,х₂) =х₁у₁+х₂у₂.

Як видно, геометричний зміст числового значення квадратичної форми Фу точці з координатамих₁іх₂– скалярний добуток.

Якщо взяти інший ортонормований базис на площині, то в ньому квадратична форма Фбуде виглядати інакше, хоча її числове значення в кожній геометричній точці й не зміниться. Якщо знайти такий базис, у якому квадратична форма не буде містити координат у першому ступені, а тільки координати у квадраті, то квадратичну форму можна буде привести до канонічного виду.

Якщо як базис взяти сукупність власних векторів лінійного перетворення, то в цьому базисі матриця лінійного перетворення має вигляд:

.

При переході до нового базису від змінних х₁іх₂ми переходимо до зміннихй. Тоді:

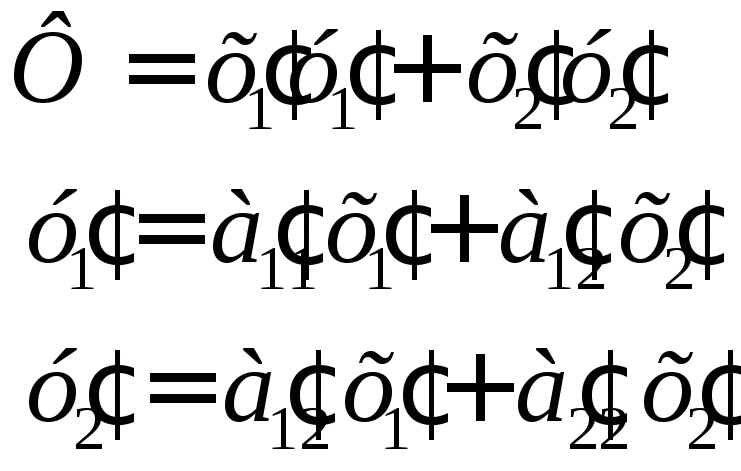
Тоді .

Вираз називаєтьсяканонічним виглядомквадратичної форми. Аналогічно можна привести до канонічного виду квадратичну форму з більшим числом змінних.

Теорія квадратичних форм використається для приведення до канонічного вигляду рівнянь кривих і поверхонь другого порядку.

Приклад.Привести до канонічного вигляду квадратичну форму

.

Коефіцієнти: а₁₁= 27,а₁₂= 5,а₂₂= 3.

Складемо характеристичне рівняння: ;

₁= 2;₂= 28;

Приклад.Привести до канонічного вигляду рівняння другого порядку:

17x²+ 12xy+ 8y²– 20 = 0.

Коефіцієнти а₁₁= 17,а₁₂= 6,а₂₂= 8.А=

Складемо характеристичне рівняння:

(17 – )(8 –) – 36 = 0

136 – 8– 17+²– 36 = 0

²– 25+ 100 = 0

₁= 5,₂= 20.

Отже: – канонічне рівняння еліпса.

Приклад. Використовуючи теорію квадратичних форм, привести до канонічного вигляду рівняння лінії другого порядку. Схематично зобразити графік.

Розв’язання:Складемо характеристичне рівняння квадратичної форми: при

Вирішивши це рівняння, одержимо ₁ = 2,₂ = 6.

Знайдемо координати власних векторів:

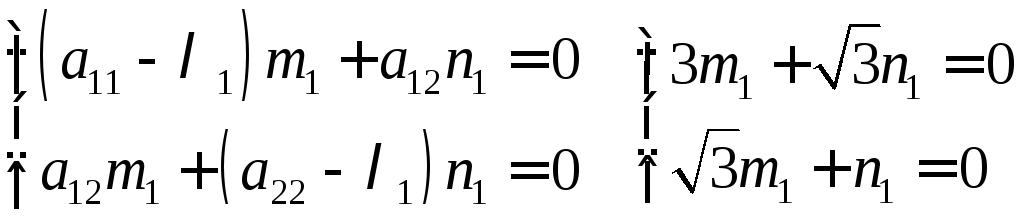приймаючиm₁ = 1, одержимоn₁ =

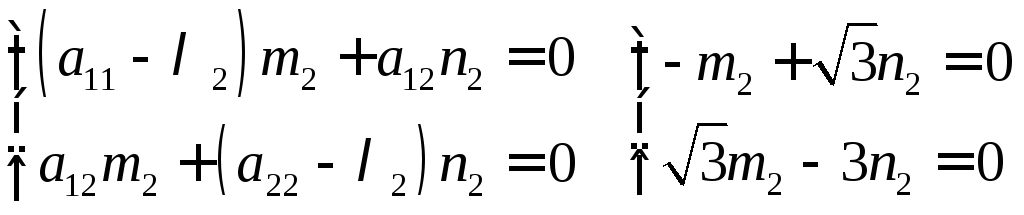приймаючиm₂ = 1, одержимоn₂ =

Власні вектори:

Знаходимо координати одиничних векторів нового базису.

Маємо наступне рівняння лінії в новій системі координат:

Канонічне рівняння лінії в новій системі координат буде мати вигляд:

Приклад. Використовуючи теорію квадратичних форм, привести до канонічного вигляду рівняння лінії другого порядку. Схематично зобразити графік.

Розв’язання:Складемо характеристичне рівняння квадратичної форми: при

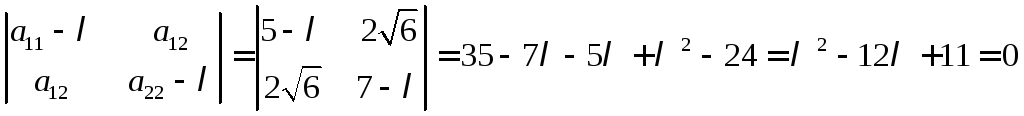
Вирішивши це рівняння, одержимо ₁ = 1,₂ = 11.

Знайдемо координати власних векторів:

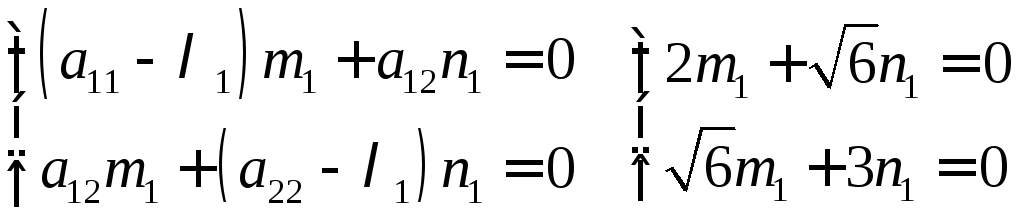приймаючиm₁ = 1, одержимоn₁ =

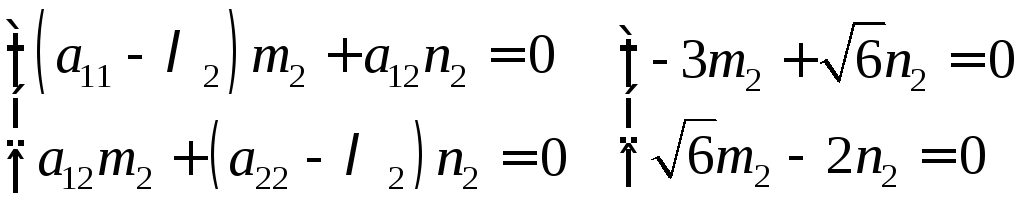приймаючиm₂ = 1, одержимоn₂ =

Власні вектори:

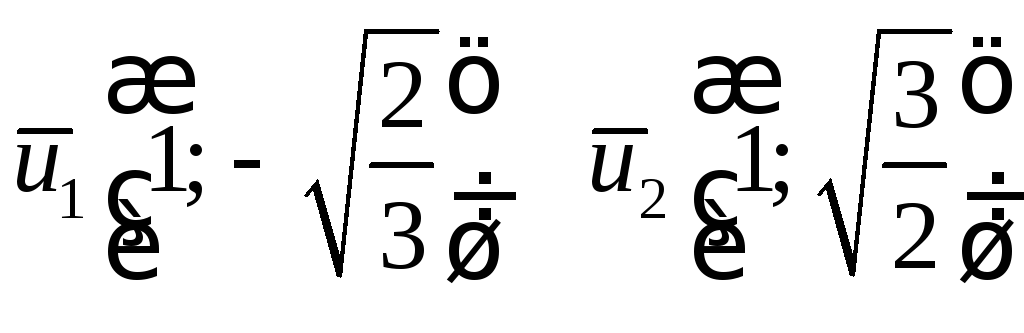
Знаходимо координати одиничних векторів нового базису.

Маємо наступне рівняння лінії в новій системі координат:

Канонічне рівняння лінії в новій системі координат буде мати вигляд:

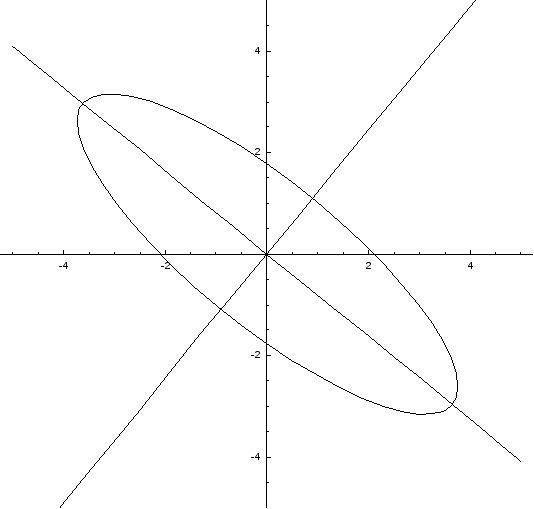
Приклад.Використовуючи теорію квадратичних форм, привести до канонічного вигляду рівняння лінії другого порядку. Схематично зобразити графік.

4ху+ 3у²+ 16 = 0

Коефіцієнти: a₁₁= 0;a₁₂= 2;a₂₂= 3.

Характеристичне рівняння:

Корені: ₁= –1,₂= 4.

Для ₁= –1 Для₂= 4

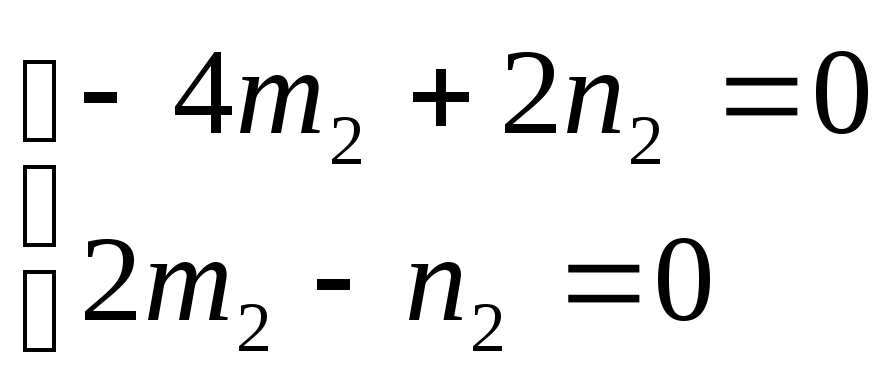
m₁= 1;n₁= –0,5;m₂= 1;n₂= 2;

= (1; –0,5)= (1; 2)

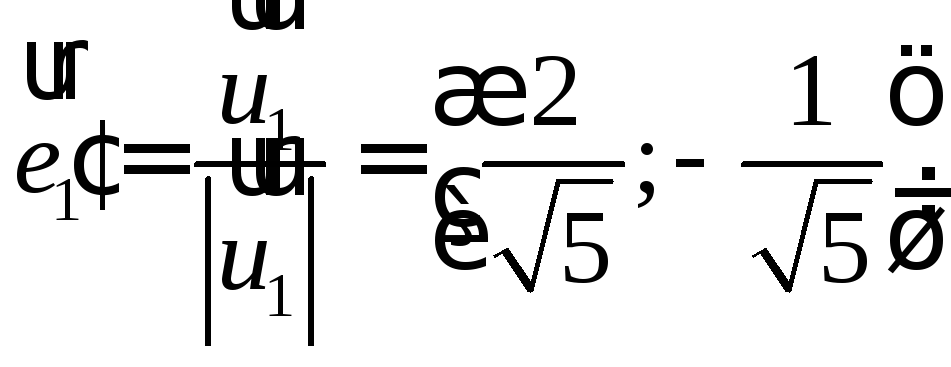
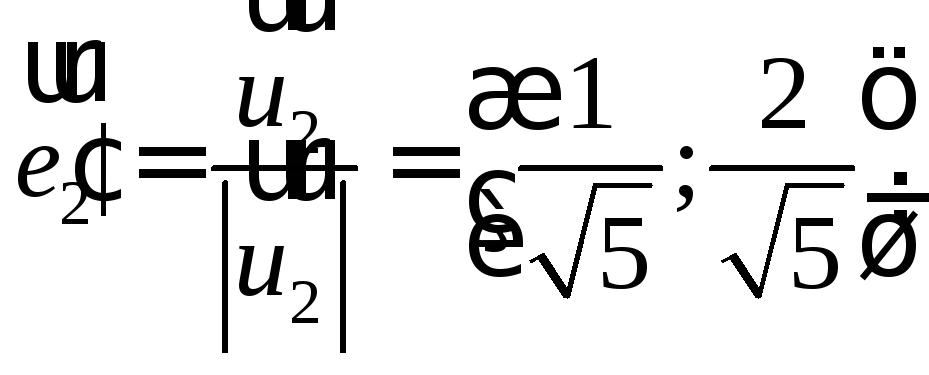
Одержуємо: – канонічне рівняння гіперболи.