Властивості еквівалентних нескінченно малих.

1.  ~ ,

2. Якщо ~і~, то~,

3. Якщо ~, то~,

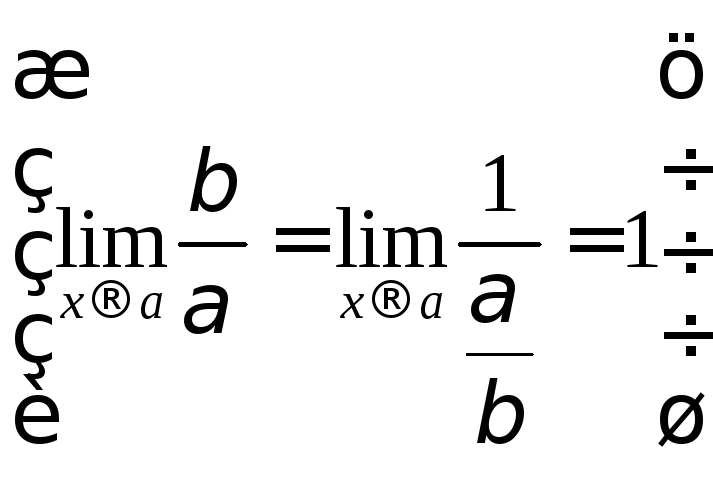
4. Якщо ~₁і~₁і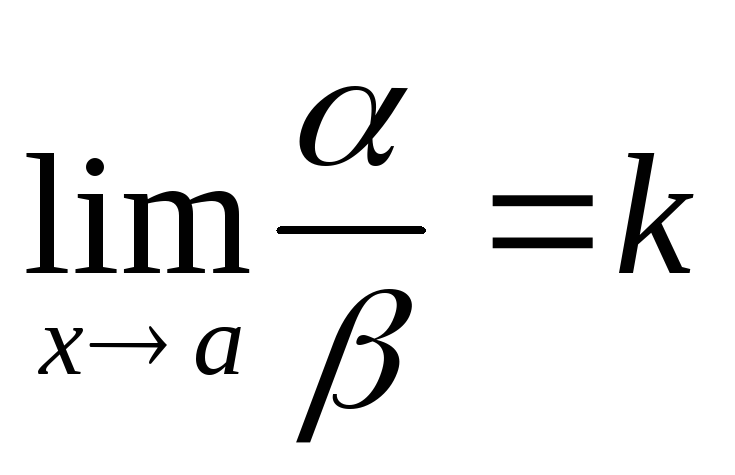, то йабо.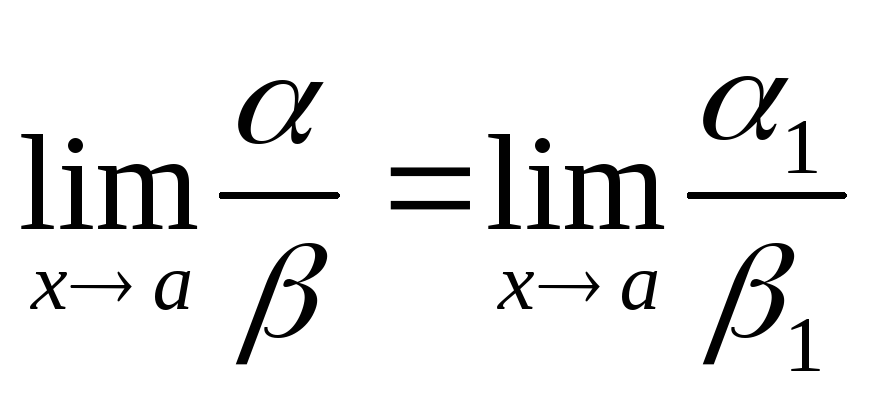

Наслідки:а) якщо~₁і, то й

б) якщо ~₁і, то

Властивість 4 особливо важливо на практиці, тому що воно фактично означає, що границя відношення нескінченно малих не міняється при заміні їх на еквівалентні нескінченно малі. Цей факт дає можливість при знаходженні границь заміняти нескінченно малі на еквівалентні їм функції, що може сильно спростити обчислення границь.

Приклад.Знайти границю

Оскільки tg5x~ 5xі sin7x~ 7xпри, то, замінивши функції еквівалентними нескінченно малими, одержимо:

Приклад.Знайти границю.

Тому що прих0, то.

Приклад.Знайти границю

Якщо і– нескінченно малі приха, причому– нескінченно мала більше високого порядку, чим, то=+– нескінченно мала, еквівалентна. Це можна довести наступною рівністю:.

Тоді кажуть, що –головна частина нескінченно малої функції.

Приклад.Функціях²+х– нескінченно мала прих0,х– головна частина цієї функції. Щоб показати це, запишемо=х²,=х, тоді

.

Деякі визначні границі.

Перша визначна границя. , деP(x) =a₀xⁿ+a₁x^n–1+…+a_n,

Q(x) =b₀x^m+b₁x^m–1+…+b_m– багаточлени.

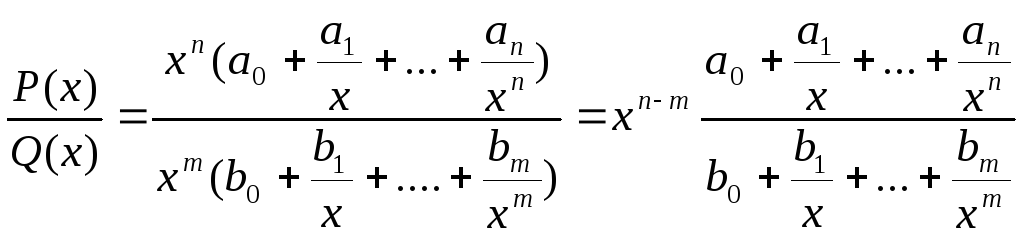
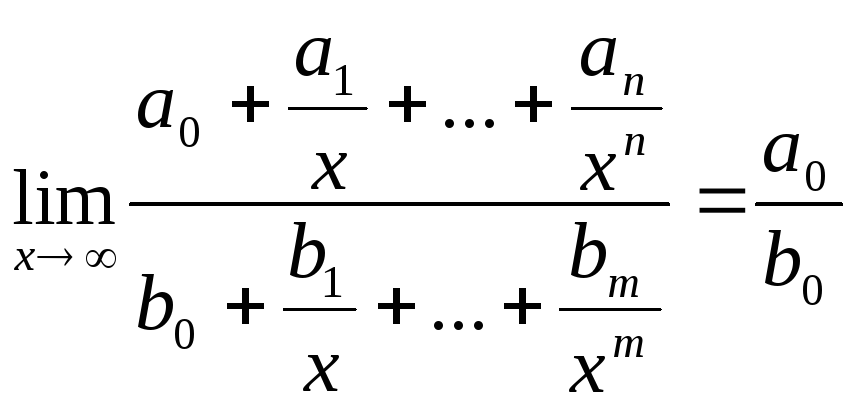
Разом:

Друга визначна границя.

Третя визначна границя.

Часто, якщо безпосереднє знаходження границі якої-небудь функції видається складним, то можна шляхом перетворення функції звести задачу до знаходження визначних меж.

Крім трьох, викладених вище, меж можна записати наступні корисні на практиці співвідношення:

Приклад.Знайти границю.

Приклад.Знайти границю.

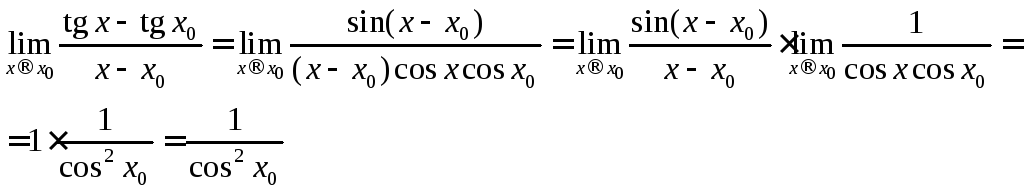
Приклад.Знайти границю.

Приклад.Знайти границю.

Приклад.Знайти границю.

Приклад.Знайти границю.

Для знаходження цієї границі розкладемо на множники чисельник і знаменник даного дробу.

x² – 6x + 8 = 0; x² – 8x + 12 = 0;

D = 36 – 32 = 4;D = 64 – 48 = 16;

x₁ = (6 + 2)/2 = 4; x₁ = (8 + 4)/2 = 6;

x₂ =(6 – 2)/2 = 2; x₂= (8 – 4)/2 = 2;

Тоді

Приклад.Знайти границю.

домножимо чисельник і знаменник дробу на спряжений вираз:=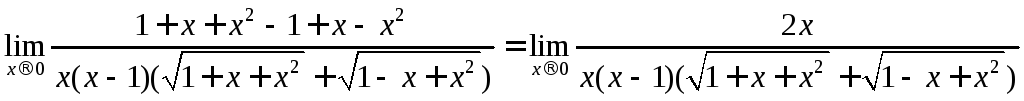

=.

Приклад.Знайти границю.

Приклад.Знайти границю.

Розкладемо чисельник і знаменник на множники.

x² – 3x +2 = (x – 1)(x – 2)

x³ – 6x² + 11x – 6 = (x – 1)(x – 2)(x – 3), тому що

x³– 6x²+ 11x– 6x– 1

x³–x²x²– 5x+ 6

– 5x²+ 11x

– 5x²+ 5x

6x– 6

6x– 6

0

x²– 5x+ 6 = (x– 2)(x– 3)

Тоді

Приклад.Знайти границю.

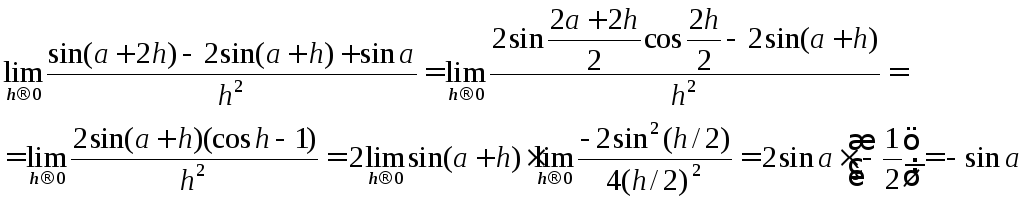
Для самостійного розв’язання:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

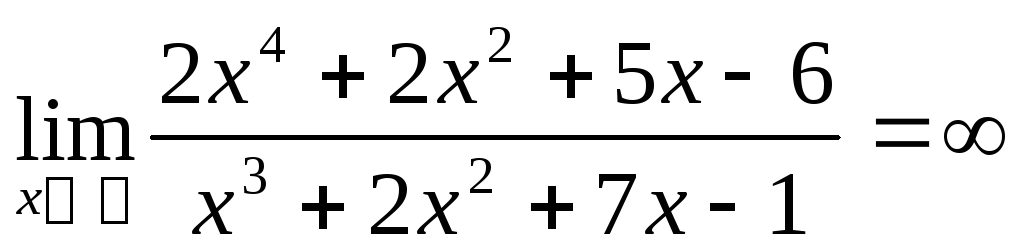
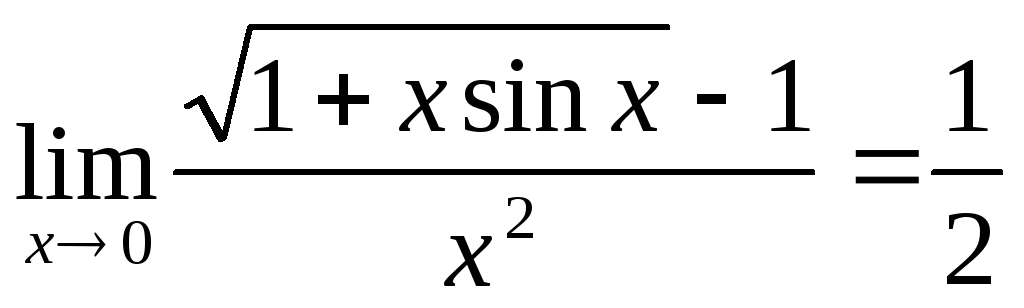
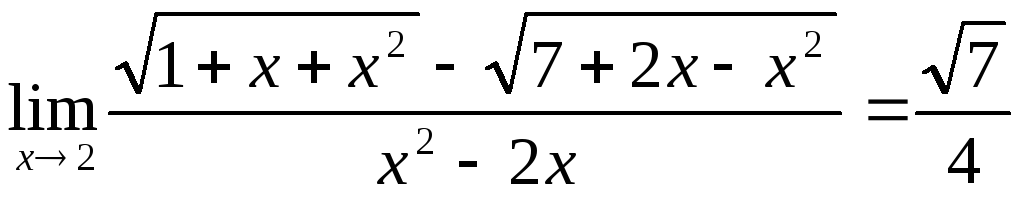
8. 8) – не визначений.

Неперервність функції в точці.

Визначення.Функціяf(x), визначена в околі деякої точких₀, називаєтьсянеперервною в точці х₀, якщо границя функції і її значення в цій точці рівні, тобто

Той же факт можна записати інакше:

Визначення.Якщо функціяf(x) визначена в деякому околі точких₀, але не є неперервною в самій точціх₀, то вона називаєтьсярозривноюфункцією, а точках₀– точкою розриву.

Приклад неперервної функції:

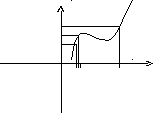y

f(x₀)+

f(x₀)

f(x₀)–

0 x₀– x₀ x₀+x

П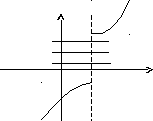риклад розривної функції:

y

f(x₀)+

f(x₀)

f(x₀)–

x₀x

Визначення.Функціяf(x) називається неперервною в точціх₀, якщо для будь-якого додатного числа> 0 існує таке число> 0, що для будь-якихх, що задовольняють умові

вірна нерівність .

Визначення.Функціяf(x) називаєтьсянеперервноюв точціх=х₀, якщо приріст функції в точціх₀є нескінченно малою величиною.

де (х) – нескінченно мала прихх₀.