Полярна система координат.

Визначення. Точка О називається полюсом, а промінь l – полярною віссю.

Суть задання який-небудь системи координат на площині полягає в тому, щоб кожній точці площини поставити у відповідність пару дійсних чисел, що визначають положення цієї точки на площині. У випадку полярної системи координат роль цих чисел грають відстань точки від полюса й кут між полярною віссю й радіус-вектором цієї точки. Цей кут  називається полярним кутом.

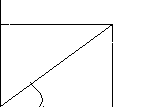
М

r

r=



О

l

Можна встановити зв'язок між полярною системою координат і декартовою прямокутною системою, якщо помістити початок декартової прямокутної системи в полюс, а полярну вісь направити уздовж додатного напрямку осі Ох.

Тоді координати довільної точки у двох різних системах координат зв'язуються співвідношеннями:

;;

Приклад.Рівняння кривої в полярній системі координат має вигляд:

. Знайти рівняння кривої в декартовій прямокутній системі координат, визначити тип кривої, знайти фокуси й ексцентриситет. Схематично побудувати криву.

Скористаємося зв'язком декартової прямокутної й полярної системи координат: ;

Одержали канонічне рівняння еліпса. З рівняння видно, що центр еліпса зсунутий вздовж осі Охна 1/2 вправо, велика піввісь a дорівнює 3/2, менша піввісьbдорівнює, половина відстані між фокусами дорівнює. Ексцентриситет дорівнюєе=с/a= 1/3. ФокусиF₁(0; 0) іF₂(1; 0).

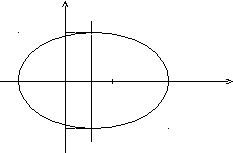
y

F₁ F₂

–1 О ½ 1 2x

–

Приклад.Рівняння кривої в полярній системі координат має вигляд:

. Знайти рівняння кривої в декартовій прямокутній системі координат, визначити тип кривої, знайти фокуси й ексцентриситет. Схематично побудувати криву.

Підставимо в задане рівняння формули, що зв'язують полярну й декартову прямокутну системи координат.

Одержали канонічне рівняння гіперболи. З рівняння видно, що гіпербола зсунута вздовж осі Охна 5 вліво, велика піввісьадорівнює 4, менша піввісьbдорівнює 3, звідки одержуємоc²=a²+b²;c= 5;e=c/a= 5/4.

Фокуси F₁(–10; 0),F₂(0; 0).

Побудуємо графік цієї гіперболи.

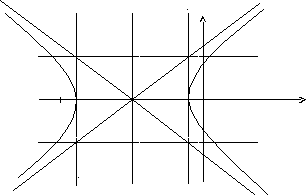
y

3

F₁ –9 –5 –1О F₂ x

–3

Аналітична геометрія в просторі. Рівняння лінії в просторі.

Як на площині, так і в просторі, будь-яка лінія може бути визначена як сукупність точок, координати яких у деякій обраній у просторі системі координат задовольняють рівнянню:

F(x,y,z) = 0.

Це рівняння називається рівнянням лінії в просторі.

Крім того, лінія в просторі може бути визначена й інакше. Її можна розглядати як лінію перетину двох поверхонь, кожна з яких задана яким-небудь рівнянням.

Нехай F(x,y,z) = 0 іФ(x,y,z) = 0 – рівняння поверхонь, що перетинаються по лініїL.

Тоді пари рівнянь

назвемо рівнянням лінії в просторі.

Рівняння прямої в просторі за точкою та напрямним вектором.

Візьмемо довільну пряму й вектор (m,n,p), паралельний даній прямій. Векторназиваєтьсянапрямним векторомпрямої.

На прямій візьмемо дві довільні точки М₀(x₀,y₀,z₀) іM(x,y,z).

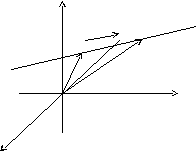z

M₁

M₀

Оy

x

Позначимо радіус-вектори цих точок як і, мабуть, що–=.

Оскільки векторийколінеарні, то вірне співвідношення=t, деt– деякий параметр.

Разом, можна записати: =+t.

Оскільки цьому рівнянню задовольняють координати будь-якої точки прямої, то отримане рівняння –параметричне рівняння прямої.

Це векторне рівняння може бути представлене в координатній формі:

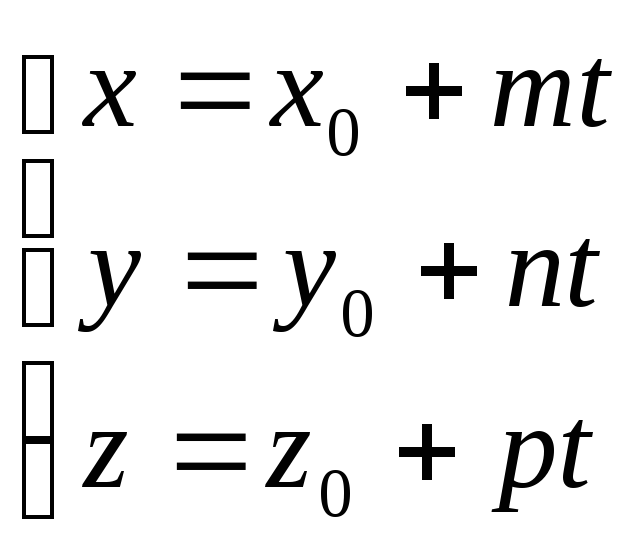
Перетворивши цю систему й дорівнявши значення параметра t, одержуємо канонічні рівняння прямої в просторі:

.

Визначення.Напрямними косинусами прямої називаються напрямні косинуси вектора, які можуть бути обчислені за формулами:

;.

Звідси одержимо: m:n:p= cos: cos: cos.

Числаm,n,pназиваютьсякутовими коефіцієнтамипрямої. Оскільки– ненульовий вектор, тоm,nіpне можуть дорівнювати нулю одночасно, але одне або два із цих чисел можуть дорівнювати нулю. У цьому випадку в рівнянні прямої варто прирівняти до нуля відповідні чисельники.