Скінченні графи й сітки. Основні визначення.

Визначення.Якщо на площині задати скінченну множинуVточок і скінченний набір лінійХ, що з'єднують деякі пари із точокV, то отримана сукупність точок і ліній буде називатисяграфом.

При цьому елементи множини Vназиваютьсявершинамиграфа, а елементи множиниХ–ребрами.

У множині Vможуть зустрічатися однакові елементи, ребра, що з'єднують однакові елементи називаютьсяпетлями. Однакові пари в множиніХназиваютьсякратними(або паралельними) ребрами. Кількість однакових пар (v,w) у Х називаєтьсякратністю ребра (v,w).

Множина Vі набірХвизначають граф із кратними ребрами –псевдограф.

G = (V, X)

Псевдограф без петель називається мультиграфом.

Якщо в наборі Хжодна пара не зустрічається більше одного разу, то мультиграф називаєтьсяграфом.

Якщо пари в наборі Х є впорядкованими, то граф називається орієнтованим або орграфом.

Графу відповідає геометрична конфігурація. Вершини позначаються точками (кружечками), а ребра - лініями, що з'єднують відповідні вершини.

Визначення.Якщох= {v, w} – ребро графа, то вершиниv, wназиваються кінцями ребрах.

Якщо х = (v, w) – дуга орграфа, то вершинаv– початок, а вершинаw– кінець дугих.

Визначення.Вершиниv, w графаG= (V,X) називаютьсясуміжними, якщо {v,w}X. Два ребра називаютьсясуміжними, якщо вони мають спільну вершину.

Визначення. Ступенемвершини графа називається число ребер, яким ця вершина належить. Вершина називаєтьсяізольованою, якщо її ступінь дорівнює одиниці йвисячою, якщо її ступінь дорівнює нулю.

Визначення. ГрафиG₁(V₁,X₁) іG₂(V₂,X₂) називаютьсяизоморфмными, якщо існує взаємно однозначне відображення:V₁V₂, що зберігає суміжність.

Визначення.Маршрутом (шляхом)для графаG(V,X) називається послідовністьv₁x₁v₂x₂v₃…x_kv_k+1... Маршрут називаєтьсязамкнутим, якщо його початкова й кінцева точки збігаються. Число ребер (дуг) маршруту (шляху) графа називаєтьсядовжиною маршруту (шляху).

Визначення.Незамкнутий маршрут (шлях) називаєтьсяланцюгом. Ланцюг, у якій всі вершини попарно різні, називаєтьсяпростим ланцюгом.

Визначення.Замкнутий маршрут (шлях) називаєтьсяциклом (контуром). Цикл, у якому всі вершини попарно різні, називаєтьсяпростим циклом.

Матриці графів.

Нехай D= (V,X) – орграф, деV= {v₁, …,v_n},X= {x₁, … ,x_m}.

Визначення.Матрицею суміжностіорграфаDназивається квадратична матрицяA(D) = [a_ij] порядкуп, у якої

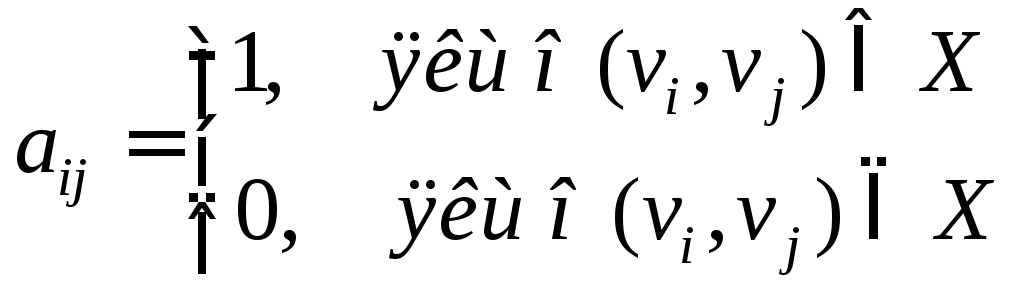
Визначення.Якщо вершинаvє кінцем ребрах, то говорять, щоvіх– інцидентні.

Визначення.Матрицею інцидентностіорграфаDназивається матриця розмірностіптB(D) = [b_ij], для якої

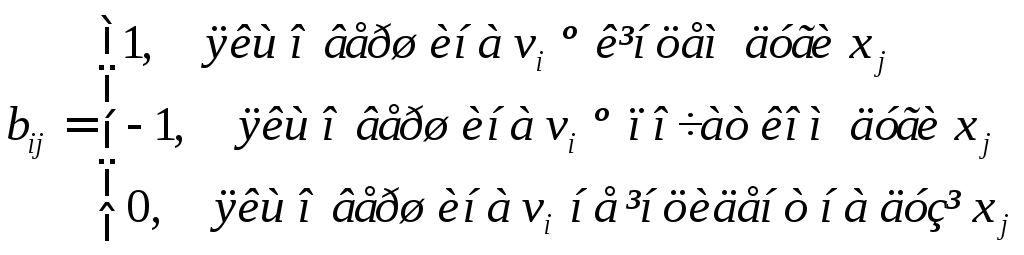
Приклад.Записати матриці суміжності й інцидентності для графа, зображеного на малюнку.

x₁

v₁ x₄ v₂

x₂

x₃

v₃

Складемо матрицю суміжності:

	v1	v2	v3
V1	0	1	0
V2	1	0	1
v3	1	0	0

Тобто – матриця суміжності.

Матриця інцидентності:

	x1	x2	x3	x4
v1	–1	0	1	1
v2	1	–1	0	–1
v3	0	1	–1	0

Тобто

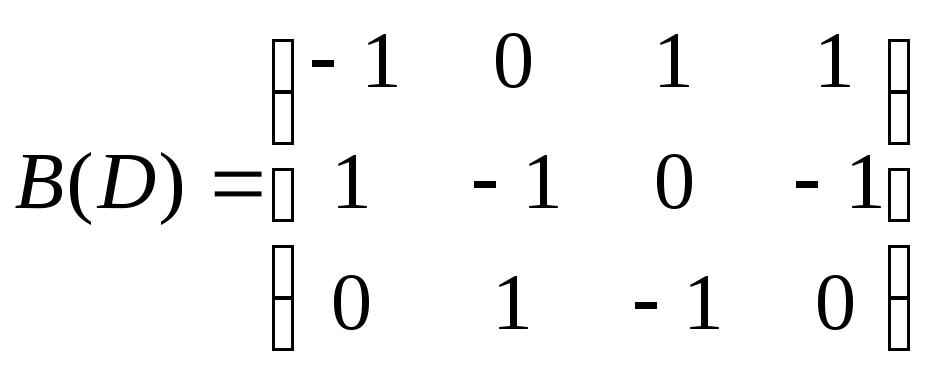
Якщо граф має кратні дуги (ребра), то в матриці суміжності приймається a_ij=k, деk– кратність дуги (ребра).

За допомогою матриць суміжності й інцидентності завжди можна повністю визначити граф і всі його компоненти. Такий метод завдання графів дуже зручний для обробки даних на ЕОМ.

Приклад.Задано симетричну матрицюQневід’ємних чисел. Намалювати на площині графG(V,X), що має заданий матрицюQсвоєю матрицею суміжності. Знайти матрицю інцидентностіRграфаG. Намалювати також орграф, що має матрицю суміжностіQ, визначити його матрицю інцидентностіС.

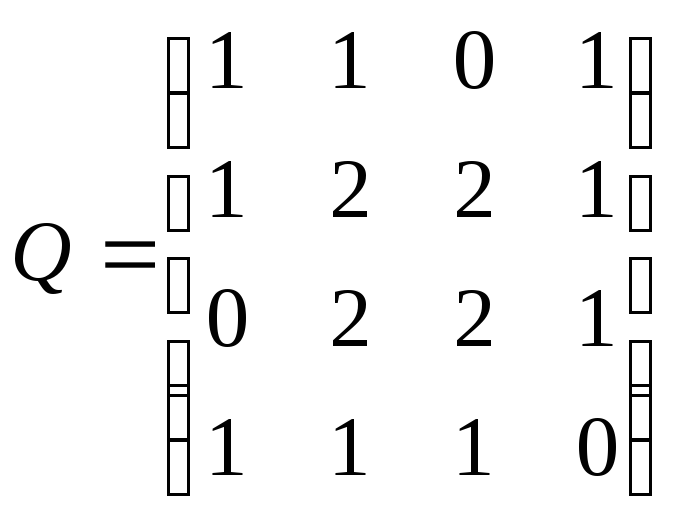
x₄

x₃

v₂

x₂x₅

x₆

x₁v₁ v₃ x₇ x₈

x₁₀

x₁₁ x₉

v₄

Складемо матрицю інцидентності:

	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11
v1	1	1	0	0	0	0	0	0	0	0	1
v2	0	1	1	1	1	1	0	0	0	1	0
v3	0	0	0	0	1	1	1	1	1	0	0
v4	0	0	0	0	0	0	0	0	1	1	1

Отже:

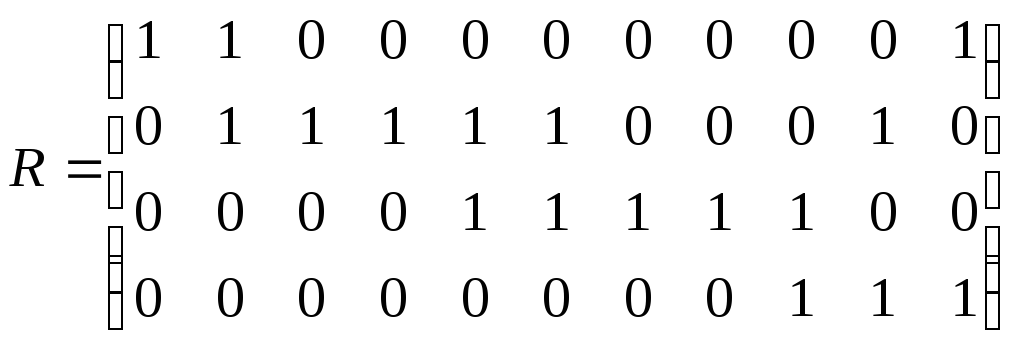
Побудуємо тепер орієнтований граф із заданою матрицею суміжності.

x₄

x₅

v₂

x₂x₇

х₃x₆

x₁v₁ х₈v₃x₁₀x₁₁

х₉

х₁₇х₁₅x₁₄

x₁₆х₁₃x₁₂

v₄

Складемо матрицю інцидентності для орієнтованого графа.

Елемент матриці дорівнює 1, якщо точка є кінцем дуги, –1 – якщо початком дуги, якщо дуга є петлею, елемент матриці запишемо як 1.

Таким чином, операції із графами можна звести до операцій з їхніми матрицями.