Рівняння прямої в просторі, що проходить через дві точки.

Якщо на прямій у просторі відзначити дві довільні точки M₁(x₁,y₁,z₁) іM₂(x₂,y₂,z₂), то координати цих точок повинні задовольняти отриманому вище рівнянню прямої:

.

Крім того, для точки М₁можна записати:

.

Вирішуючи спільно ці рівняння, одержимо:

.

Це рівняння прямої, що проходить через дві точки в просторі.

Загальні рівняння прямої в просторі.

Рівняння прямої може бути розглянуте як рівняння лінії перетину двох площин.

Як було розглянуто вище, площина у векторній формі може бути задана рівнянням:

+ D = 0, де

– нормаль площини;– радіус-вектор довільної точки площини.

Нехай у просторі задані дві площини: +D₁= 0 і+D₂= 0, вектори нормалі мають координати:(A₁,B₁,C₁),(A₂,B₂,C₂);(x,y,z).

Тоді загальні рівняння прямої у векторній формі:

Загальні рівняння прямої в координатній формі:

Практична задача часто полягає в приведенні рівнянь прямих у загальному виді до канонічного виду.

Для цього треба знайти довільну точку прямої й числа m,n,p.

При цьому напрямний вектор прямої може бути знайдений як векторний добуток векторів нормалі до заданих площин.

Приклад.Знайти канонічне рівняння, якщо пряма задана у вигляді:

Для знаходження довільної точки прямій, приймемо її координату х= 0, а потім підставимо це значення в задану систему рівнянь.

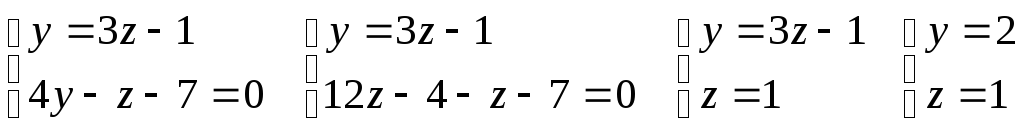, тобтоА(0, 2, 1).

Знаходимо компоненти напрямного вектора прямої.

Тоді канонічні рівняння прямої:

Приклад.Привести до канонічного виду рівняння прямої, задане у вигляді:

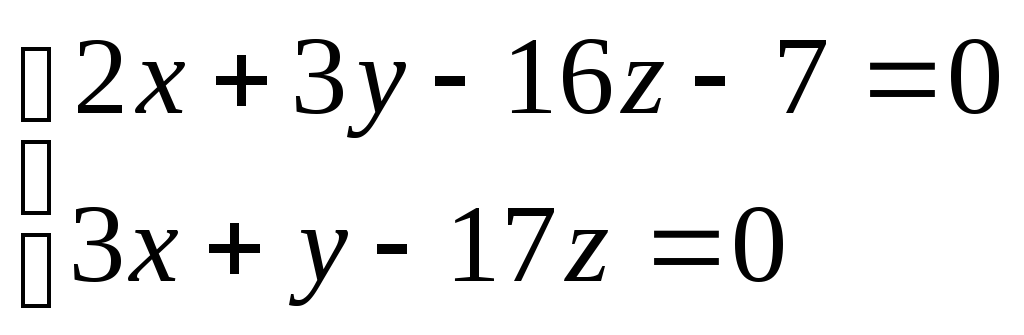
Для знаходження довільної точки прямої, що є лінією перетину зазначених вище площин, приймемо z= 0. Тоді:

;

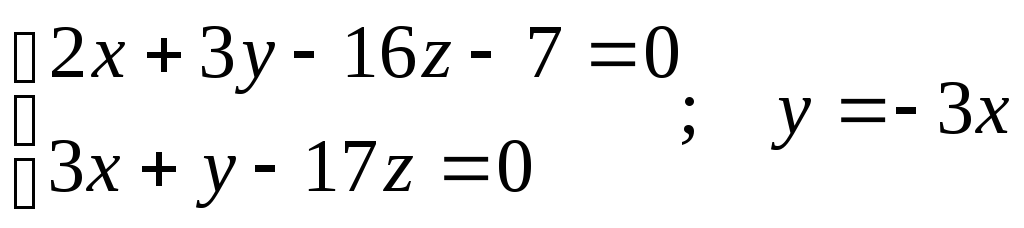2x– 9x –7 = 0;

x= –1;y= 3;

Одержуємо: A(–1; 3; 0).

Напрямний вектор прямої: .

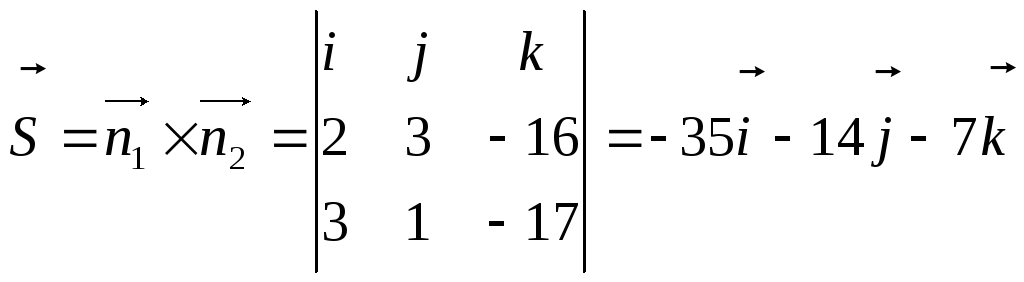Отже:

Кут між площинами.

₁О

Кут між двома площинами в просторі пов'язаний з кутом між нормалями до цих площин₁співвідношенням:=₁або= 180⁰– ₁, тобто cos=cos₁.

Визначимо кут ₁. Відомо, що площини можуть бути задані співвідношеннями:

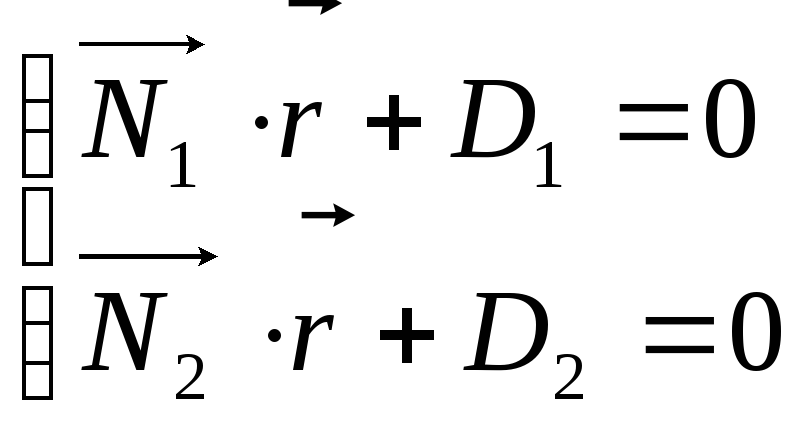, де

(A₁,B₁,C₁),(A₂,B₂,C₂). Кут між векторами нормалі знайдемо з їхнього скалярного добутку:

.

Таким чином, кут між площинами знаходиться за формулою:

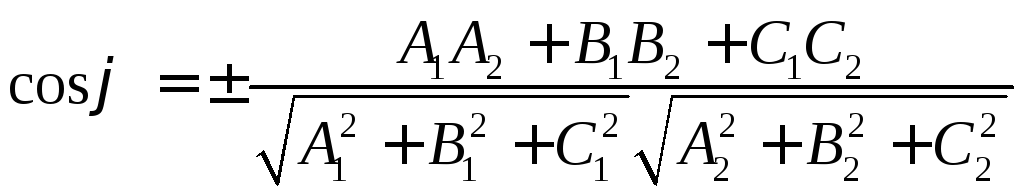
Вибір знака косинуса залежить від того, який кут між площинами слід знайти – гострий, або суміжний з ним тупий.

Умови паралельності й перпендикулярності

площин.

На основі отриманої вище формули для знаходження кута між площинами можна знайти умови паралельності й перпендикулярності площин.

Для того, щоб площини були перпендикулярні необхідно й достатньо, щоб косинус кута між площинами дорівнював нулю. Ця умова виконується, якщо:

.

Площини паралельні, вектори нормалей колінеарні:.Ця умова виконується, якщо:.

Кут між прямими в просторі.

Нехай у просторі задані дві прямі. Їхні параметричні рівняння:

l₁:

l₂:

Кут між прямими і кут між напрямними векторамицих прямих пов'язані співвідношенням:=₁або= 180⁰–₁. Кут між напрямними векторами знаходиться зі скалярного добутку у такий спосіб:

.

Умови паралельності й перпендикулярності

прямих у просторі.

Щоб дві прямі були паралельні необхідно й достатньо, щоб напрямні вектори цих прямих були колінеарні, тобто їх відповідні координати були пропорційні.

Щоб дві прямі були перпендикулярні необхідно й достатньо, щоб напрямні вектори цих прямих були перпендикулярні, тобто косинус кута між ними дорівнює нулю.

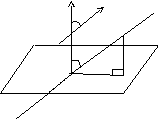
Кут між прямою й площиною.

Визначення. Кутом між прямою й площиною називається будь-який кут між прямою та її проекцією на цю площину.







Нехай площина задана рівнянням , а пряма –. З геометричних міркувань (див. мал.) видно, що шуканий кут= 90⁰–, де– кут між векторамий. Цей кут може бути знайдений за формулою:

У координатній формі:

Умови паралельності й перпендикулярності

прямої і площині в просторі.

Для того, щоб пряма й площина були паралельні, необхідно й достатньо, щоб вектор нормалі до площини й напрямний вектор прямої були перпендикулярні. Для цього необхідно, щоб їх скалярний добуток був рівний нулю.

Для того, щоб пряма й площина були перпендикулярні, необхідно й достатньо, щоб вектор нормалі до площини й напрямний вектор прямої були колінеарні. Ця умова виконується, якщо векторний добуток цих векторів був дорівнює нулю.

Поверхні другого порядку.

Визначення.Поверхні другого порядку – це поверхні, рівняння яких у прямокутній системі координат є рівняннями другого порядку.

Циліндричні поверхні.

Визначення.Циліндричними поверхнями називаються поверхні, утворені лініями, паралельними до якоїсь фіксованої прямої.

Розглянемо поверхні, у рівнянні яких відсутня складова z, тобто напрямні паралельні осіОz. Тип лінії на площиніхOу(ця лінія називається напрямної поверхні) визначає характер циліндричної поверхні. Розглянемо деякі окремі випадки залежно від рівняння напрямних:

1. - еліптичний циліндр.

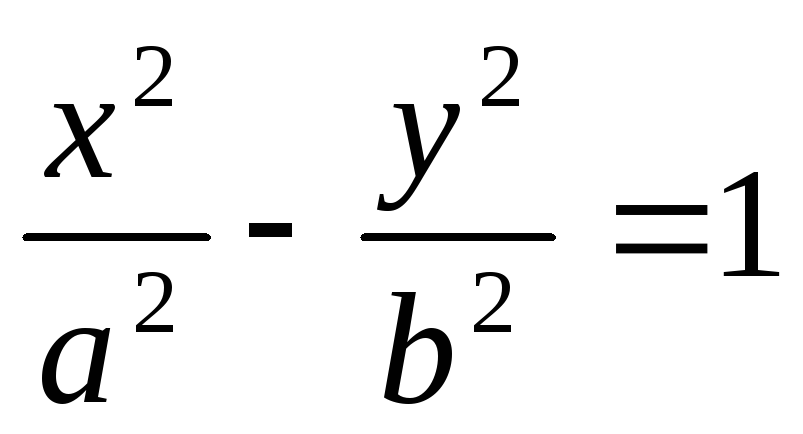2. – гіперболічний циліндр.

3. x² = 2py– параболічний циліндр.

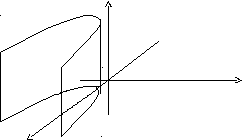
Поверхні обертання.

Визначення.Поверхня, описана деякою лінією, що обертається навколо нерухомої прямоїd, називаєтьсяповерхнею обертання з віссю обертанняd.

Якщо рівняння поверхні в прямокутній системі координат має вигляд: , то ця поверхня – поверхня обертання з віссю обертанняОz. Аналогічно:– поверхня обертання з віссю обертанняОу,– поверхня обертання з віссю обертанняОх.

Запишемо рівняння поверхонь обертання для деяких окремих випадків:

1. -еліпсоїд обертання

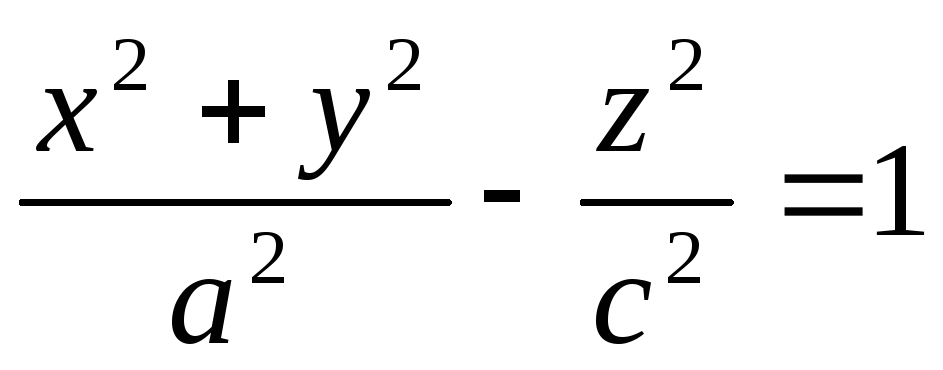2. -однопорожнинний гіперболоїд обертання

3. -двопорожнинний гіперболоїд обертання

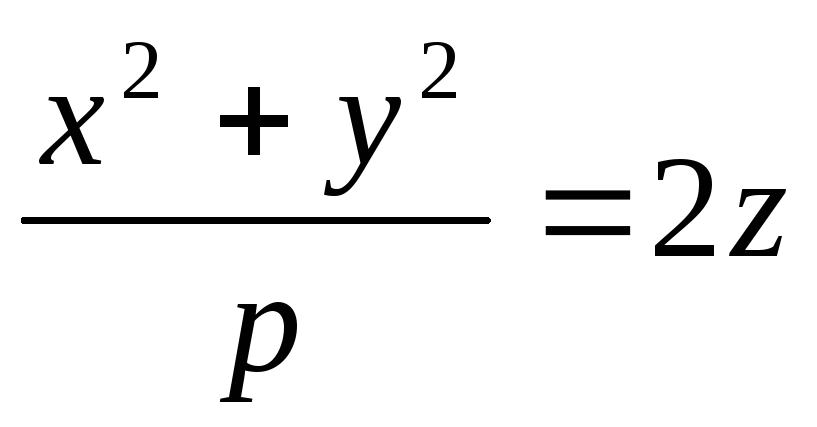4. -параболоїд обертання

Аналогічно можуть бути записані рівняння для розглянутих вище поверхонь обертання, якщо осями обертання є осі Ох або Оу.

Однак, перераховані вище поверхні є всього лише окремими випадками поверхонь другого порядку загального виду, деякі типи яких розглянуті нижче:

Сфера:

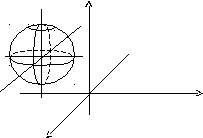
Тривісний еліпсоїд:

У перетині еліпсоїда площинами, паралельними координатним площинам, виходять еліпси з різними осями.

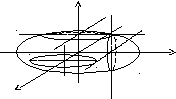
Однопорожнинний гіперболоїд:

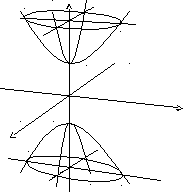
Двопорожнинний гіперболоїд:

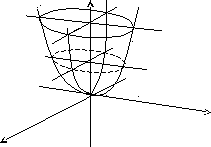
Еліптичний параболоїд:

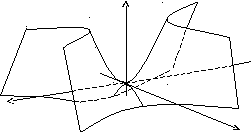
Гіперболічний параболоїд:

Конус другого порядку:

Циліндрична й сферична системи координат.

Як і на площині, у просторі положення будь-якої точки може бути визначене трьома координатами в різних системах координат, відмінних від декартової прямокутної системи. Циліндрична й сферична системи координат є узагальненням для простору полярної системи координат, що була докладно розглянута вище.

Введемо в просторі точку Ои проміньl, що виходить із точкиО, а також вектор. Через точкуОможна провести єдину площину, перпендикулярну вектору нормалі.

Для введення відповідності між циліндричною, сферичною й декартовою прямокутною системами координат точку Осуміщають з початком декартової прямокутної системи координат, проміньl– з позитивним напрямком осіх, вектор нормалі – з віссюz.

Циліндрична й сферична системи координат використовуються в тих випадках, коли рівняння кривій або поверхні в декартовій прямокутній системі координат виглядають досить складно, і операції з таким рівнянням виглядають трудомісткими.

Подання рівнянь у циліндричній і сферичній системі дозволяє значно спростити обчислення, що буде показано далі.

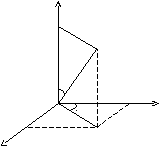
z

М



 h

О  x

r

M₁

y

ОМ₁=r;MM₁=h;

Якщо з точки Мопустити перпендикулярММ₁на площину, то точкаМ₁буде мати на площині полярні координати (r,).

Визначення. Циліндричними координатами точкиМназиваються числа (r,,h), які визначають положення точкиМу просторі.

Визначення. Сферичними координатами точки М називаються числа (r,,), де– кут міжі нормаллю.