Матриці лінійних перетворень.

Нехай в n-мірному лінійному просторі з базисом, ,…,задано лінійне перетворенняА. Тоді векториА, А,…,А - також вектори цього простору і їх можна представити у вигляді лінійної комбінації векторів базису:

A =a₁₁ +a₂₁ +…+a_n1

A =a₁₂ +a₂₂ +…+a_n2

……………………………….........

A =a_n1 +a_n2 +…+a_nn

Тоді матриця А=називаєтьсяматрицею лінійного перетворення А.

Якщо в просторі Lвзяти вектор=x₁ +x₂ +…+x_n, тоA L.

, де

……………………………......

Ці рівності можна назвати лінійним перетворенням у базисі ,,…,... У матричному вигляді:

,А,

Приклад.Знайти матрицю лінійного перетворення, заданого у вигляді:

A=

На практиці дії над лінійними перетвореннями зводяться до дій над їхніми матрицями.

Визначення:Якщо векторпереводиться у векторлінійним перетворенням з матрицеюА, а вектору векторлінійним перетворенням з матрицеюВ, те послідовне застосування цих перетворень рівносильне лінійному перетворенню, що переводить вектору вектор(воно називаєтьсядобутком складових перетворень).

С = ВА

Приклад.Задано лінійне перетворенняА, що переводить вектору векторі лінійне перетворенняВ, що переводить вектору вектор. Знайти матрицю лінійного перетворення, що переводить вектору вектор.

С = ВА

Тобто

Примітка:ЯкщоА= 0, то перетворення вироджене, тобто, наприклад, площина перетвориться не в цілу площину, а в пряму.

Власні значення й власні вектори лінійного перетворення.

Визначення:НехайL– заданийn-мірний лінійний простір. Ненульовий векторLназиваєтьсявласним векторомлінійного перетворенняА, якщо існує таке число, що виконується рівність:

.

При цьому число називаєтьсявласним значенням (характеристичним числом)лінійного перетворенняА, що відповідає вектору.

Визначення:Якщо лінійне перетворенняАв деякому базисі,,…,має матрицюА=, то власні значення лінійного перетворенняАможна знайти як корінь₁,₂, …, _nрівняння:

Це рівняння називаєтьсяхарактеристичним рівнянням,а його ліва частина –характеристичним багаточленомлінійного перетворенняА.

Слід зазначити, що характеристичний багаточлен лінійного перетворення не залежить від вибору базису.

Розглянемо окремий випадок. НехайА– деяке лінійне перетворення площини, матриця якого дорівнює. Тоді перетворенняАможе бути задане формулами:

;

у деякому базисі .

Якщо перетворення Амає власний вектор із власним значенням, то.

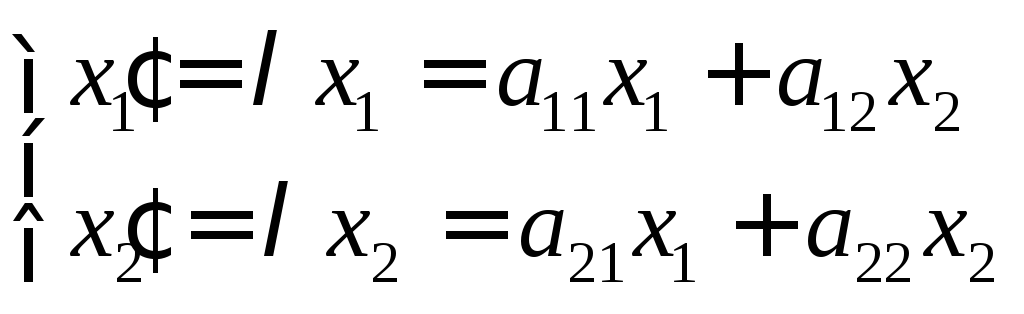або

Оскільки власний вектор ненульовий, тох₁іх₂не дорівнюють нулю одночасно. Оскільки дана система однорідна, то для того, щоб вона мала нетривіальний розв’язок, визначник системи повинен дорівнювати нулю. У протилежному випадку за правилом Крамера система має єдиний розв’язок – нульовий, що неможливо.

Отримане рівняння єхарактеристичним рівнянням лінійного перетворення А.

Таким чином, можна знайти власний вектор (х₁,х₂) лінійні перетворенняАс власним значенням, де– корінь характеристичного рівняння, ах₁іх₂– корінь системи рівнянь при підстановці в неї значення.

Зрозуміло, що якщо характеристичне рівняння не має дійсних коренів, то лінійне перетворення А не має власних векторів.

Слід зазначити, що якщо – власний вектор перетворенняА, то й будь-який вектор колінеарний йому – теж власний з тим же самим власним значенням.

Дійсно,. Якщо врахувати, що вектори мають один початок, то ці вектори утворять так званийвласний напрямок абовласну пряму.

Оскільки характеристичне рівняння може мати два різних дійсних корені ₁і₂, то в цьому випадку при підстановці їх у систему рівнянь одержимо нескінченну кількість розв’язків. (Оскільки рівняння лінійно залежні). Ця множина розв’язків визначає двівласні прямі.

Якщо характеристичне рівняння має два рівних корені₁=₂=, то або є лише одна власна пряма, або при підстановці в систему вона перетворюється в систему виду:. Ця система задовольняється будь-якими значеннямих₁іх₂. Тоді всі вектори будуть власними, і таке перетворення називаєтьсяперетворенням подібності.

Приклад.Знайти характеристичні числа й власні вектори лінійного перетворення з матрицеюА=.

Запишемо лінійне перетворення у вигляді:

Складемо характеристичне рівняння:

;

Корені характеристичного рівняння: ₁= 7;₂= 1;

Для кореня ₁= 7:

Із системи виходить залежність: x₁ – 2x₂ =0. Власні вектори для першого кореня характеристичного рівняння мають координати:(t; 0,5t)деt –параметр.

Для кореня ₂= 1:

Із системи виходить залежність: x₁ + x₂ =0. Власні вектори для другого кореня характеристичного рівняння мають координати:(t; –t)деt –параметр.

Отримані власні вектори можна записати у вигляді:

Приклад.Знайти характеристичні числа й власні вектори лінійного перетворення з матрицеюА=.

Запишемо лінійне перетворення у вигляді:

Складемо характеристичне рівняння:

;

Корінь характеристичного рівняння: ₁=₂= 2;

Одержуємо:

Із системи виходить залежність: x₁ – x₂ =0. Власні вектори для першого кореня характеристичного рівняння мають координати:(t; t)деt –параметр.

Власний вектор можна записати: .

Розглянемо інший окремий випадок. Якщо– власний вектор лінійного перетворенняА, заданого в тривимірному лінійному просторі, ах₁,х₂,х₃– компоненти цього вектора в деякому базисі, то

,

де – власне значення (характеристичне число) перетворенняА.

Якщо матриця лінійного перетворення Амає вигляд:

, то

Характеристичне рівняння:

Розкривши визначник, одержимо кубічне рівняння відносно . Будь-яке кубічне рівняння з дійсними коефіцієнтами має або один, або три дійсних корені.

Тоді будь-яке лінійне перетворення в тривимірному просторі має власні вектори.

Приклад.Знайти характеристичні числа й власні вектори лінійного перетворенняА, матриця лінійного перетворенняА=.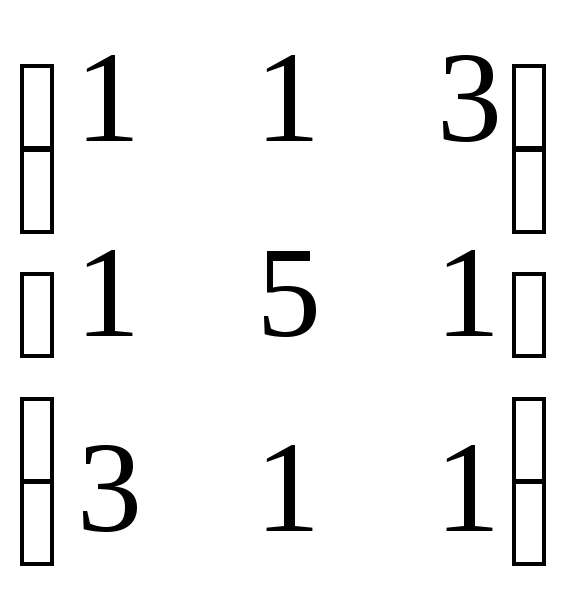

Складемо характеристичне рівняння:

Власні значення: ₁= –2;₂= 3;₃= 6;

1) Для ₁= –2:

Якщо прийняти х₁= 1, тох₂= 0;x₃= – 1;

Власні вектори:

2) Для ₂= 3:

Якщо прийняти х₁= 1, тох₂= –1;x₃= 1;

Власні вектори:

3) Для ₃= 6: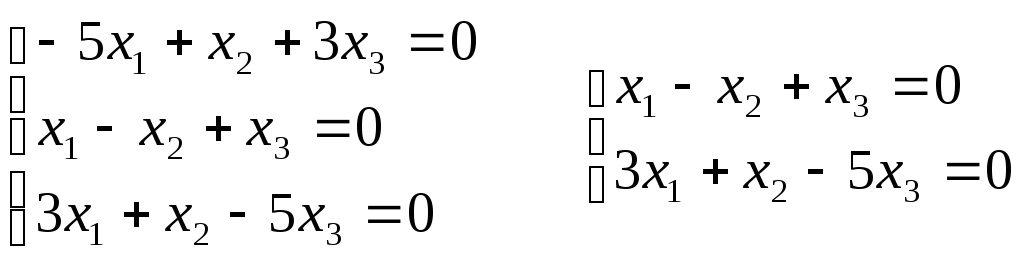

Якщо прийняти х₁= 1, тох₂= 2;x₃= 1;

Власні вектори:

Приклад.Знайти характеристичні числа й власні вектори лінійного перетворенняА, матриця лінійного перетворенняА=.

Складемо характеристичне рівняння:

₁= 0;₂= 1;₃= –1;

Для ₁= 0:

Якщо прийняти х₃= 1, одержуємох₁= 0,х₂= –2

Власні вектори t, деt– параметр.

Для самостійного розв’язання:Аналогічно знайтийдля₂і₃.