Досяжність і зв’язність.

Визначення.Вершинаwграфа D (або орграфа) називаєтьсядосяжноюз вершиниv, якщо абоw=v, або існує шлях зv в w(маршрут, що з'єднуєv іw).

Визначення.Граф (орграф) називаєтьсязв'язним, якщо для будь-яких двох його вершин існує маршрут (шлях), що їх зв'язує. Орграф називаєтьсяодносторонньо зв'язним, якщо для будь-яких двох його вершин принаймні одна досяжна з іншої.

Визначення.ПсевдографомD(V,X),асоційованимз орієнтованим псевдографом, називається псевдографG(V,X₀) у якомуХ₀виходить ізХзаміною всіх упорядкованих пар (v, w) на неупорядковані пари (v, w).

Визначення. Орграф називаєтьсяслабко зв'язним, якщо зв'язним є асоційований з ним псевдограф.

Ейлерові й гамільтонові графи.

Визначення.Ланцюг (цикл) у псевдографіGназиваєтьсяЕйлеровим, якщо він проходить по одному разу через кожне ребро псевдографаG.

Теорема.Для того, щоб зв'язний псевдограф G мав Ейлеровий цикл, необхідно й достатньо, щоб ступені його вершин були парними.

Теорема.Для того, щоб зв'язний псевдограф G володів Ейлеровим ланцюгом, необхідно й достатньо, щоб він мав рівно дві вершини непарного ступеня.

Визначення.Цикл (ланцюг) у псевдографіGназиваєтьсягамільтоновим, якщо він проходить через кожну вершину псевдографаGрівно один раз.

Приклад.

– у графі є й Ейлерів і гамільтонів цикли

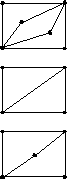
– у графі є Ейлерів цикл, але немає гамільтонового

– у графі є гамільтоновий, але немає Ейлерового циклу

– у графі немає ні Ейлерового, ні гамільтонового циклу

Граф G називається повним, якщо кожна його вершина суміжна з усіма іншими вершинами. У повному графі завжди існують гамільтонові цикли.

Також необхідною умовою існування гамільтонового циклу є зв’язність графа.

Дерева й цикли.

Визначення.Граф G називаєтьсядеревом, якщо він є зв'язним і не має циклів. ГрафG, усі компоненти зв’язності якого є деревами, називаєтьсялісом.

У графа, що є деревом, число ребер на одиницю менше числа вершин. Дерево не містить циклів, будь-які дві його вершини можна з’єднати єдиним простим ланцюгом.

Якщо в дерева Gє, принаймні, одне ребро, то в ньому обов'язково знайдеться висяча вершина, тому що в противному випадку в графі буде цикл.

Для графів, які самі по собі не є деревами, вводиться поняття кістякового дерева.

Визначення.Кістяковим деревом зв'язного графаGназивається будь-який його підграф, що містить всі вершини графаGі є деревом.

Нехай G– зв'язний граф. Тоді кістякове дерево графаG(якщо воно існує) повинне міститиn(G)–1 ребер.

Таким чином, будь-яке кістякове дерево графа Gє результат видалення із графаGрівноm(G) – (n(G) – 1) =m(G) –n(G) + 1 ребер.

Число v(G) =m(G) –n(G) + 1 називаєтьсяцикломатичним числомзв'язного графаG.

Однією з найпоширеніших задач є задача побудови кістякового дерева мінімальної довжини графа. Для розв’язання цієї задачі застосовується наступний алгоритм.

1) Оберемо в графі Gребро мінімальної довжини. Разом з інцидентними йому вершинами воно утворить підграфG₂.

2) Будуємо граф G₃, додаючи до графаG₂нове ребро мінімальної довжини, обране серед ребер графаG, кожне з яких інцидентне якійсь з вершин графаG₂, і одночасно інцидентне якійсь з вершин графаG, що не міститься в графіG₂.

3) Будуємо графи G₄,G₅, …,G_n, повторюючи дії пункту 2 доти, доки не переберемо всі вершини графаG.

Приклад.Визначити мінімальне кістякове дерево навантаженого графа.

Граф називається навантаженим, якщо на множині його дуг задана деяка функція, що називаєтьсяваговоюфункцією, і визначає довжину дуги.

У нашому прикладі – вагова функція визначає довжини дуг числами 1, 2, 3, 4, 5.

v₂2v₃

1 4

1 v₅3

5 3

v₁4v₄

2 2

1 1 1 1 1 1 1 3

G₂G₃G₄G₅

На четвертому кроці алгоритму одержали дерево G₅, що з'єднує всі вершини вихідного графа. Таким чином, деревоG₅, буде мінімальним кістяковим деревом графаG.