Елементи математичної логіки.

Математична логіка – різновид формальної логіки, тобто науки, що вивчає умовиводи з погляду їхньої формальної будови.

Визначення.Висловлюваннямназивається пропозиція, до якого можливо застосувати поняття істинне або неправдиве.

У математичній логіці не розглядається сам зміст висловлень, визначається тільки його істинність або хибність, що прийнято позначати відповідно І або Н.

Зрозуміло, що істині й помилкові висловлювання утворять відповідні множини. За допомогою простих висловлень можна складати складніші, з'єднуючи прості висловлювання сполучниками “і”, “або”.

Таким чином, операції з висловлюваннями можна описувати за допомогою деякого математичного апарата.

Вводяться наступні логічні операції (зв'язування) над висловлюваннями

1. Заперечення. Запереченням висловлюванняРназивається висловлювання, що істинне тільки тоді, коли висловлюванняРнеправдиве.

Позначається Рабо.

Відповідність між висловлюваннями визначається таблицями істинності. У нашому випадку ця таблиця має вигляд:

P	Р
І	Н
Н	І

2) Кон’юнкція.Кон’юнкцією двох висловлюваньPіQназивається висловлювання, істинне тоді й тільки тоді, коли істинні обоє висловлювань.

Позначається P&QабоРQ.

P	Q	P&Q
І	І	І
І	Н	Н
Н	І	Н
Н	Н	Н

3) Диз'юнкція.Диз'юнкцією двох висловленьPіQназивається висловлювання, помилкове тоді й тільки тоді, коли обоє висловлювання помилкові.

Позначається PQ.

P	Q	PQ
І	І	І
І	Н	І
Н	І	І
Н	Н	Н

4) Імплікація.Імплікацією двох висловленьPіQназивається висловлювання, неправдиве тоді й тільки тоді, коли висловлюванняРістинне, аQ– неправдиве.

Позначається PQ(абоРQ). ВисловлюванняРназивається посилкою імплікації, а висловлюванняQ– наслідком.

P	Q	PQ
І	І	І
І	Н	Н
Н	І	І
Н	Н	І

5) Еквіваленція.Еквіваленцією двох висловленьPіQназивається висловлювання, істинне тоді й тільки тоді, коли істинність висловлювань збігається.

Позначається РQ або РQ.

P	Q	PQ
І	І	І
І	Н	Н
Н	І	Н
Н	Н	І

За допомогою цих основних таблиць істинності можна скласти таблиці істинності складних формул.

Приклад.За допомогою таблиць істинності перевірити, чиєеквівалентними формулиіψ.

Складемо таблиці істинності для кожної формули:

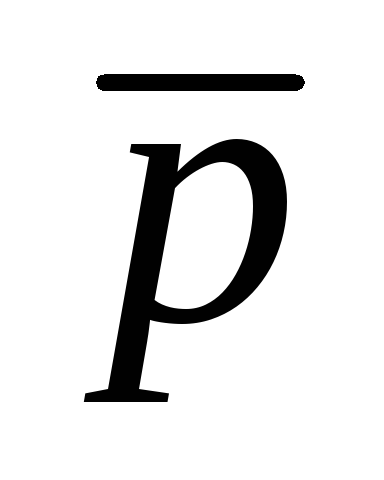
p	r		(pr)
І	І	Н	І	І
І	Н	Н	Н	І
Н	І	І	Н	Н
Н	Н	І	Н	Н

p	r
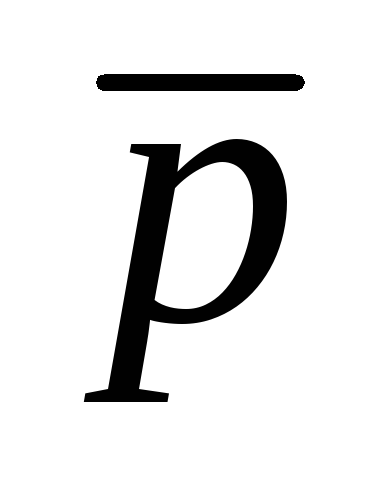
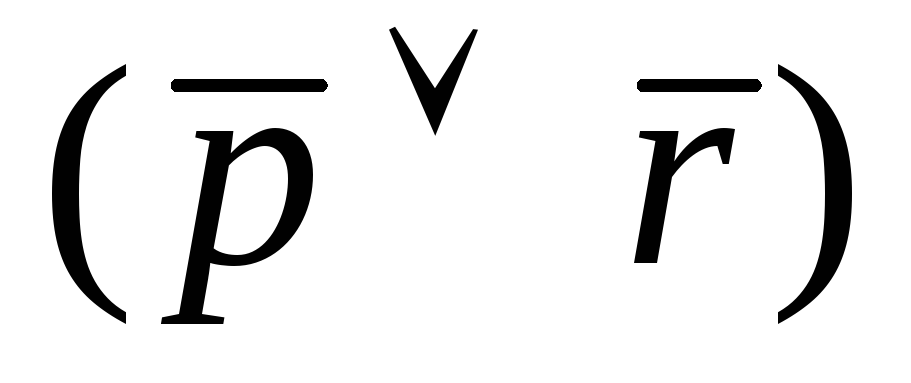
І	І	Н	Н	Н	І
І	Н	Н	І	І	І
Н	І	І	Н	І	І
Н	Н	І	І	І	І

Дані формули не є еквівалентними.

Приклад.За допомогою таблиць істинності перевірити, чиєеквівалентними формулиіψ.

Складемо таблиці істинності для заданих формул.

p	q	r	pq	(pq)r
І	І	І	І	І
І	І	Н	І	І
І	Н	І	Н	І
І	Н	Н	Н	Н
Н	І	І	Н	І
Н	І	Н	Н	Н
Н	Н	І	І	І
Н	Н	Н	І	І

p	q	r	pq	qp	(pq)(qp)	(pq)(qp)r
І	І	І	І	І	І	І
І	І	Н	І	І	І	І
І	Н	І	Н	І	І	І
І	Н	Н	Н	І	І	І
Н	І	І	І	Н	І	І
Н	І	Н	І	Н	І	І
Н	Н	І	І	І	І	І
Н	Н	Н	І	І	І	І

Зі складених таблиць видно, що дані формули не еквівалентні.