6. Расслоение множества на классы эквивалентности.

Итак, для множества М, имеющего размерность n: каждому элементу а, принадлежащему М (аМ), соответствует n-ка параметров (а₁, а₂, …, а_n). Зафиксируем какой-либо параметр, например а_n=0. Тогда подмножество М₁М (для элементов, где а_n=0). Следовательно, размерность множества М₁ равна (n-1), то есть элемент из множества М₁ определяется набором (n-1) параметров, «чисел».

Поскольку имеется бесчисленное однопараметрическое множество способов, которыми можно зафиксировать параметр а_n, то, следовательно, множество М расчленяется на однопараметрическое множество (n-1)-мерных подмножеств, каждое из которых соответствует одному из этих однопараметрических значений параметра а_n, причем никакие два из этих подмножеств не пересекаются, и объединение всех этих подмножеств есть множество М.

Такие подмножества называются классами эквивалентности, означающими, что элементам а и b, принадлежащим множеству М, отнесены n-ки чисел (а₁, а₂, …, а_n), (b₁, b₂, …, b_n), в которых а_n=b_n. Для фиксированной координаты и₁ в вышеприведенном примере такими классами эквивалентности являются непересекающиеся 2-поверхности.

Если фиксируются два параметра, то из множества М выделяется (n-2)-мерное подмножество. Выполняя перебор всех двухпараметрических способов фиксации этих двух параметров, мы получаем двупараметрическое семейство прямых, параллельных оси y.

В общем случае, фиксируя разm каких-то параметров, мы расслаиваем n-мерное множество М на классов поэлементов в каждом.

Таким образом, если множество М разбить на взаимно непересекающихся и заполняющих все множестваМ₁ подмножеств по элементов в каждом, тоМ содержит:

. (7)

ПРИМЕР. Множество плоскостей пространства расслаивается на пучков параллельных плоскостей поплоскостей в пучке, то есть содержит.

7. Использование уравнений. Далее рассмотрим, как осуществляется подсчет параметрического числа поверхности, если последняя задана в аналитической форме. Для простоты начнем исследование с 2-поверхностей пространства Е₃.

Рассматривая уравнение типа Ах+By+Cz+D=0, можно подсчитать размерность многообразия, а именно множество плоскостей пространства. Если мы придадим коэффициентам А, В, С, D определенные числовые значения А₀, В₀, С₀, D₀, то мы получим некоторую определенную плоскость αМ. Таким образом, имеется соответствие: «четверка чисел» (А₀, В₀, С₀, D₀)плоскость пространстваα₀, которое однозначно лишь в одном направлении.

Действительно, плоскости α₀ отвечает любая из четверок коэффициентов kA, kB, kC, kD, где k – любое число, не равное нулю. То есть уравнения:

А₀х+B₀y+C₀z+D₀=0;

kА₀х+kB₀y+kC₀z+kD₀=0

задают одну и ту же плоскость. Итак, одной четверке чисел соответствует одна плоскость, но одной плоскости соответствует однопараметрическое множество четверок чисел (столько же, сколько чисел k), соответственно пропорциональных четверок. Отношение «быть соответственно пропорциональным» является отношением эквивалентности на множестве четверок чисел. Поэтому четырехпараметрическое множество четверок чисел расслаивается на трехпараметрическое многообразие классов по однопараметрическому семейству пропорциональных четверок в каждом.

Таким образом, соответствие «класс пропорциональных четверок чисел – плоскость пространства» однозначно уже в обе стороны, и поэтому плоскостей в множестве М столько же, сколько таких классов, то есть - трехпараметрическое множество.

Если координаты x, y, z связаны двумя уравнениями, то этим выделяется одномерное подмножество трехмерного множества точек пространства – линия (в общем случае пространственная).

8. Размерность кривых, поверхностей. Параметрическое число Р плоской алгебраической кривой m-го порядка:

. (8)

ПРИМЕР 1. Параметрическое число кривой второго порядка m=2 (например, коники): ,то есть, чтобы на плоскости выделить конику, нужно задать пять параметров.

В общем случае параметрическое число алгебраической поверхности m-го порядка:

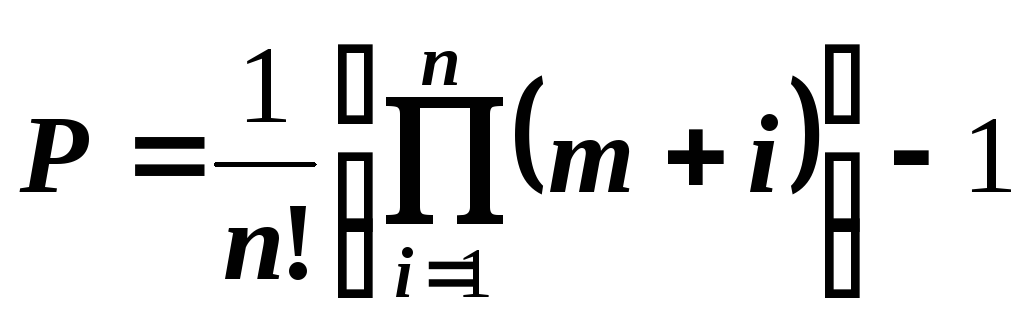, (9)

где n – размерность объемлющего пространства; m – порядок поверхности.

ПРИМЕР 2. Поверхность второго порядка m=2 в трехмерном пространстве n=3 имеет следующее параметрическое число:

.

В приведенных выше примерах каждый коэффициент эквивалентен заданию одного условия. Поэтому говорят, что кривая второго порядка, будучи пятипараметрической, однозначно определяется заданием пяти точек, а поверхность второго порядка – заданием девяти точек.