Розділ 2. Задачі лінійного програмування

2.1 Попередні відомості теорії лінійного програмування.

Задача математичного програмування (1.3) або (1.4) називається задачею лінійного програмування (ЛП), якщо цільова функція f є лінійною функцією, а множина допустимих рішень Х задається лінійними нерівностя­ми або рівняннями

min(max) f(x)=c₁x₁+c₂x₂+…+c_nx_n (2.1)

a₁₁x₁+a₁₂x₂+…+a_1nx_n ≤ b₁;

a₂₁x₁+a₂₂x₂+…+a_2nx_n ≤ b₂; (2.2)

…………………………

a_k1x₁+a_k2x₂+…+a_knx_n ≤ b_k;

x₁ ≥ 0,…, x_n ≥ 0 , (2.3)

або у векторному вигляді

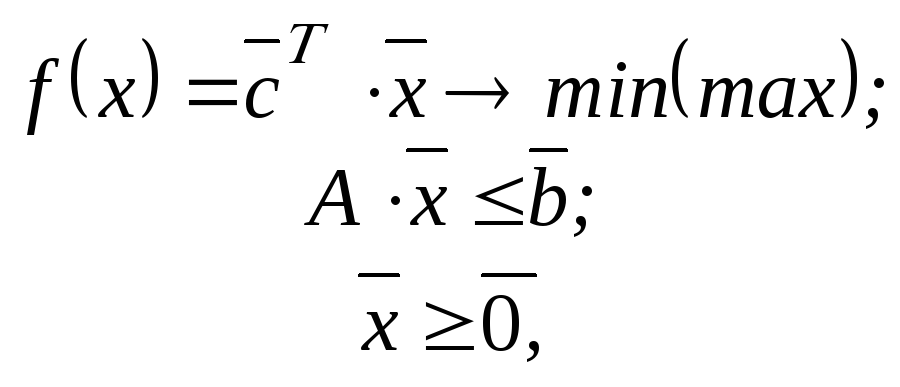(2.4)

де

А = {,...,};,…,;;.

Наведена модель є стандартною постановкою задачі ЛП, у якій в системі обмежень (2.2) можуть бути різні відношення типу “ > ”, “ > ”, “ = ”. Тут c₁,…,c_n – коефіцієнти при цільовій функції, a₁₁,...,a_nn – коефіцієнти при змінних в системі обмежень, b₁,…,b_k – вільні члени системи обмежень. Усі ці компоненти задачі ЛП є відомими (заданими) числами. Невідомими (шуканими) змінними будуть елементи вектора {x₁,…,x_n}^T. При цьому задача ЛП полягає у тому щоб знайти такі значення змінних x₁*,...,x_n* (точку мінімуму (максимуму)), щоб вони, по-перше задовольняли обмеження (2.2) і (2.3) (умова допустимості), а, по-друге, щоб у точці х* = (х₁*,...,x_n*) цільова функція f приймала мінімальне (максимальне) значення f(x*) (умова оптимальності). Аналогічно ставиться задача на мінімум.

Крім стандартної форми запису задачі ЛП є також загальна і канонічна форми запису. Загальна форма запису аналогічна стандартній за винятком того, що на значення вектору шуканих змінних {x₁,…,x_n}^T не накладено ніяких обмежень за знаком.

У канонічній формі задач ЛП треба знайти екстремум цільової функції за си­стемою обмежень, що описуються рівняннями та за умови невід’єм­ності усіх шуканих змінних:

;

;

.

Між формами запису задач ЛП є правила переходу. Розглянемо правила переходу від загальної форми до канонічної. У системі обмежень нерівності типу перетворюються у рівності шляхом додавання до її лівої частини додаткової невід’ємної змін­ної . Так само перетворюються у рівності нерівності типу шляхом віднімання від їх лівих частин додаткової невід’ємної змінної. При цьому слід зауважити, що умовулегко звести до, помноживши кожну нерівність на -1, аналогічно тому як обмеження типуможна звести до обмежень типупомноживши їх на -1 та замінивши знак змінних,. Кожну змінну, на знак якої не накладено обмежень, можна описати як різницю двох невід’ємних змінних де,,. При цьому обмеження типу, де , можна перетворити в рівність за правилом: , де .

Приклад 2.1. Звести до канонічної таку загальну задачу ЛП:

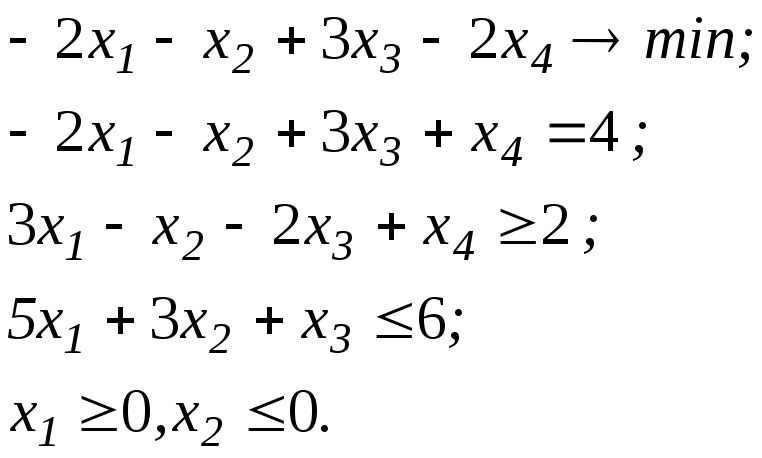
Введемо додаткові змінні x₅  0 та x₆  0 в друге і третє обмеження-нерівності. Крім того, замінимо x^'₂= - x₂  0, а змін­ні x₃ та x₄, що не обмежені за знаком, запишемо у вигляді x₃= x'₃- x''₃, де x'₃, x''₃  0; x₄= x'₄- x''₄, де x'₄, x''₄  0. Таким чином, зводимо задачу до вигляду:

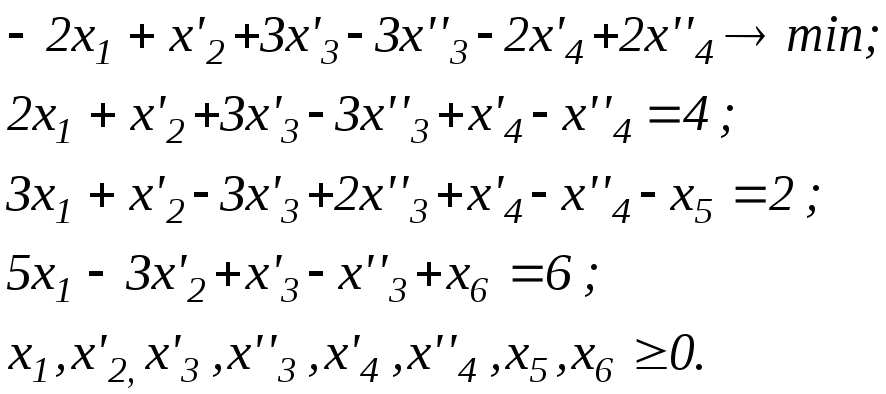
Приклад 2.2. Перехід від канонічної форми запису задачі ЛП до стандартної. Структура задачі ЛП залежить від рангу r системи обмежень. Якщо r < n, то n-r змінним, які називають небазисними, можна надавати будь-які значення, при цьому r змінні, що називаються базисними, можна визначити через небазисні. Розглянемо канонічну задачу ЛП:

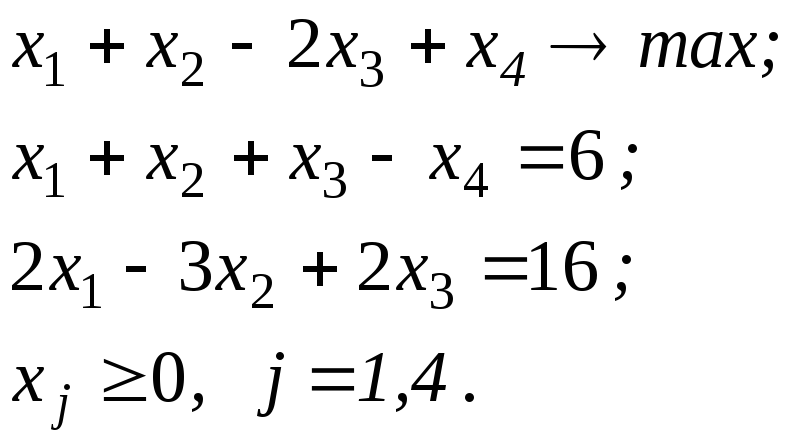
Ранг системи обмежень дорівнює двом. Тому за небазисні змінні виберемо, наприклад, х₁ та х₄. Визначимо через них базисні змінні x₂ та x₃:

.

Оскільки х₁ та х₄ невід’ємні, то: 8+3/2x₂ - x₃  0; 2+5/2x₂  0. При цьому цільова функція від небазисних змінних набуде такого вигляду:

10 +5x₂ –3x₃  max.

Запишемо тепер задачу у стандартній формі:

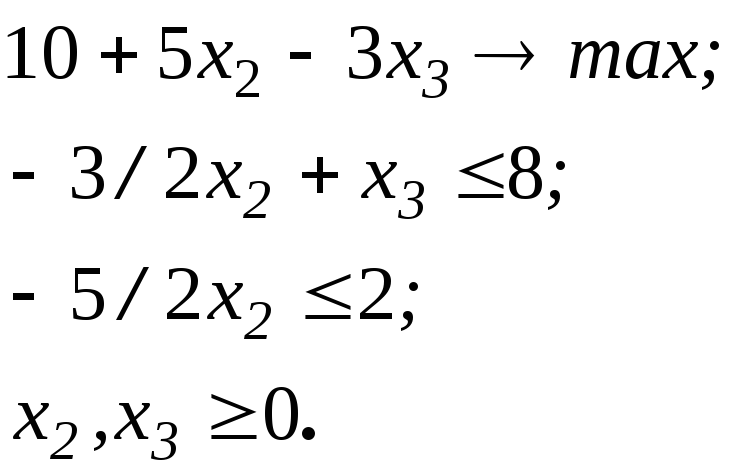
У векторному вигляді задача перетворення у канонічну форму запису буде мати такий вигляд. Якщо система обмежень задана у формі , то можна, увівши додаткові змінні, звести її до вигляду

, ,,

де . Якщо ж обмеження задані у формі, то

, ,.

Розглянемо тепер задачу з обмеженнями . Цю систему обмежень можна представити у вигляді системи

.

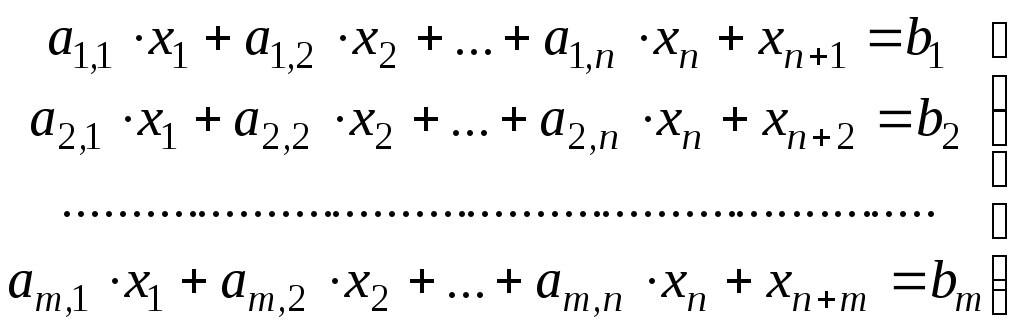Введемо такі позначення:

, ,…,,,…,,...

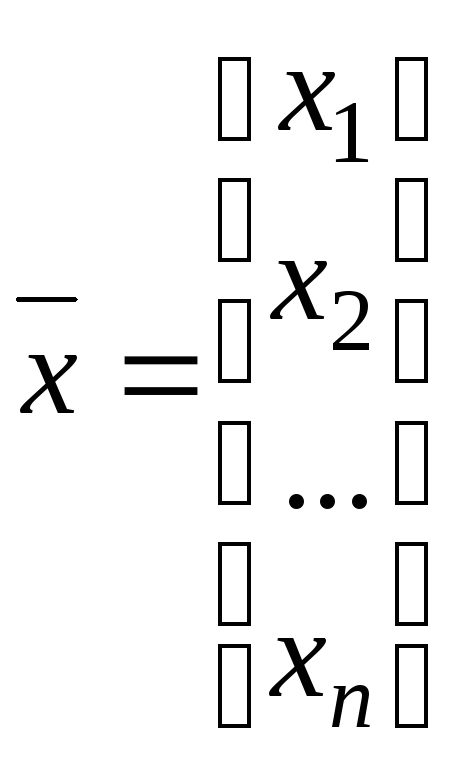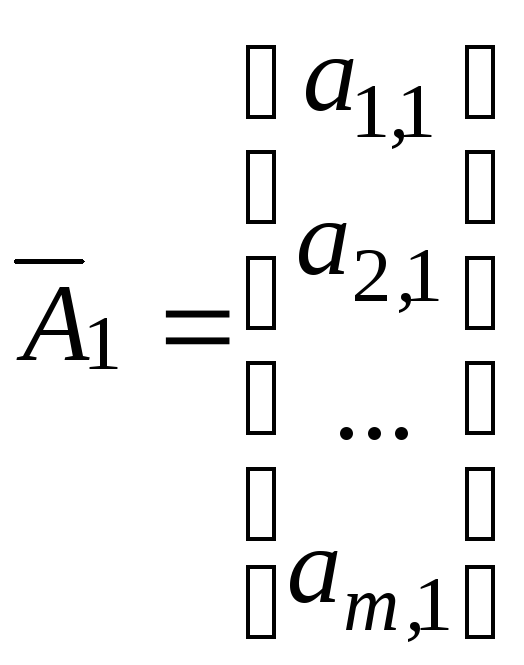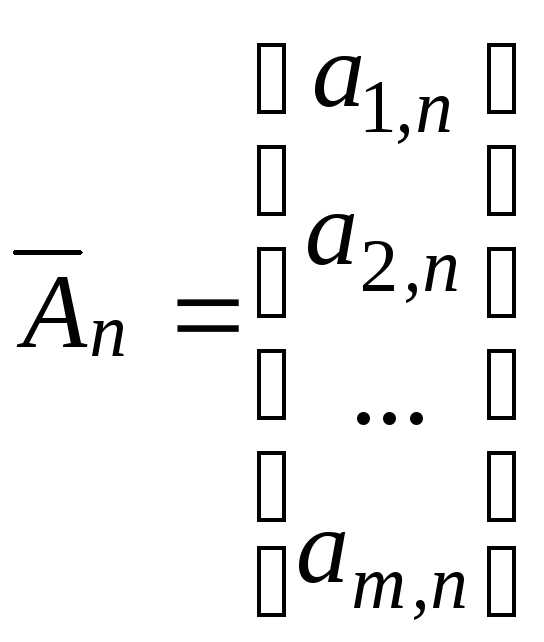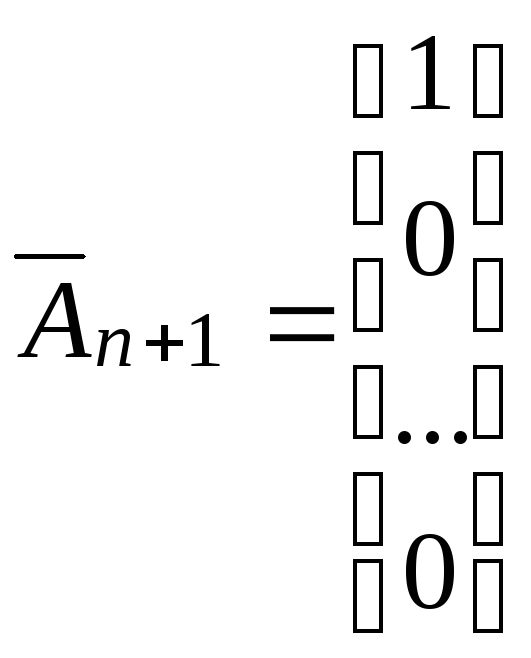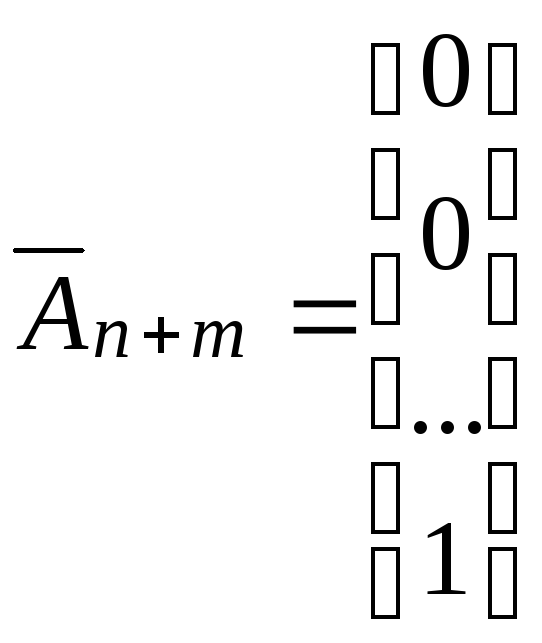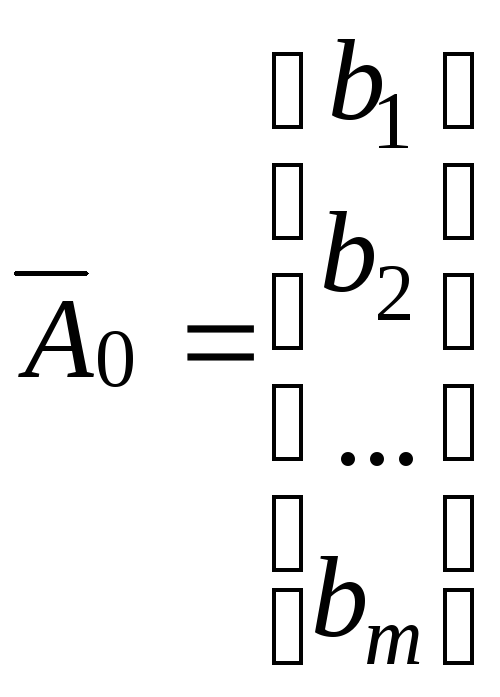Тоді канонічну задачу ЛП можна записати у вигляді:

,

.

Вектори називаються векторами умов, а сама задача ЛП називається розширеною щодо вихідної задачі. Нехайі- допустимі множини рішень вихідної і розширеної задач відповідно. Тоді будь-якій точці множинивідповідає єдина точка множиниі навпаки. У загальному випадку, допустима множинавихідної задачі є проекцією множинирозширеної задачі на підпростір вихідних змінних.

Означення 2.1. Набір чисел , що задовольняє обмеженням задачі лінійного програмування, називається їїпланом.

Означення 2.2. Розв’язком задачі лінійного програмування називається її план, що мінімізує (або максимізує) лінійну форму.

Уведемо поняття базисного розв’язку. З матриці розширеної задачі виберемолінійно незалежних векторів-стовпців, що позначимо як матрицю, а черезпозначимо матрицю із стовпців, що залишилися. Тоді, і обмеження розширеної задачі лінійного програмування можна записати у виді:

. (2.5)

Очевидно, що стовпці матриці утворять базис-мірного простору. Тому векторі будь-який стовпець матриціможна представити у вигляді лінійної комбінації стовпців матриці.

Помножимо зліва обидві частини виразу (2.5) на матрицю , що є матрицею, оберненою щодо матриціВ , і як результат отримаємо

, (2.6)

звідки знайдемо вектор розв’язку :

. (2.7)

Для різних значень , будемо отримувати різні розв’язки, і якщо покласти, що, то будемо мати

. (2.8)

Розв’язок (2.8) називають базисним розв’язком системи з рівнянь зневідомими.

Якщо отриманий розв’язок містить тільки додатні компоненти, то такий розв’язок називається допустимим базисним розв’язком.

Особливість допустимих базисних розв’язків полягає у тому, що вони є крайніми точками допустимої множини розширеної задачі.

Якщо серед компонентів немає нульових, то допустимий базисний розв’язок називаєтьсяневиродженим.

Означення 2.3. План задачі лінійного програмування будемо називати опорним, якщо вектори умовз додатними коефіцієнтами лінійно незалежні.

Тобто опорний план – це допустимий базисний розв’язок розширеної системи і є кутовою точкою багатокутника рішень.

Означення 2.4. Опорний план називається невиродженим, якщо він містить додатних компонентів (по числу обмежень).

Невироджений опорний план утворюється перетинанням гіперплощин зn+m гіперплощин, що утворюють допустиму область розв’язків. У випадку виродженості в кутовій точці багатокутника розв’язків перетинається більше гіперплощин.

Теорема 2.1. (Основна теорема лінійного програмування):

1. Лінійна форма 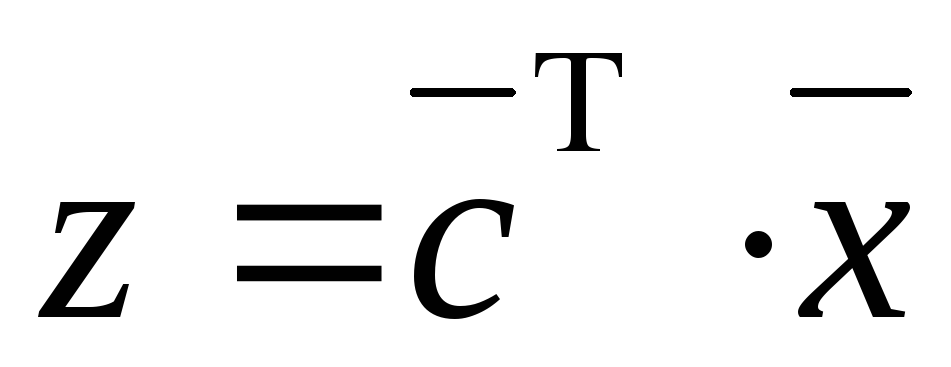досягає свого мінімуму в кутовій точці багатокутника рішень.

2. Якщо вона приймає мінімальне значення більше ніж в одній кутовій точці, то вона досягає того ж самого значення у будь-якій точці, що є опуклою комбінацією цих кутових точок.

Доведення. Доведення теореми засновано на такій лемі.

Лема. Якщо – замкнена, обмежена і опукла множина, що має скінчене число крайніх (кутових) точок, то будь-яка точкаможе бути представлена у вигляді опуклої комбінації крайніх точок.

1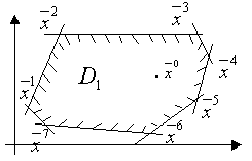) Нехай- деяка внутрішня точка (див. на рисунку зліва). Багатокутник обмежений, замкнений і має скінчене число кутових точок.– допустима множина.

Припустимо, що є оптимальною точкою, тобто,. Припустимо, також, що точкане є кутовою. Тоді на підставі леми точкуможна визначити через кутові точки багатокутника, тобто,,.

Оскільки функція лінійна, то

. (*)

Виберемо серед точок ту, у якій лінійна формаприймає найменше значення. Нехай це буде точка. Позначимо мінімальне значення функції в кутовій точці через:

.

Підставимо це значення в лінійну форму (*) замістьі отримаємо

.

Оскільки, за припущенням, – оптимальна точка, то ми отримали протиріччя:. Отже,,- кутова точка.

2) Припустимо, що лінійна форма приймає мінімальне значення більш ніж в одній кутовій точці, наприклад, у кутових точках. Тоді якщоє опуклою комбінацією цих точок, тобто

, і,

то 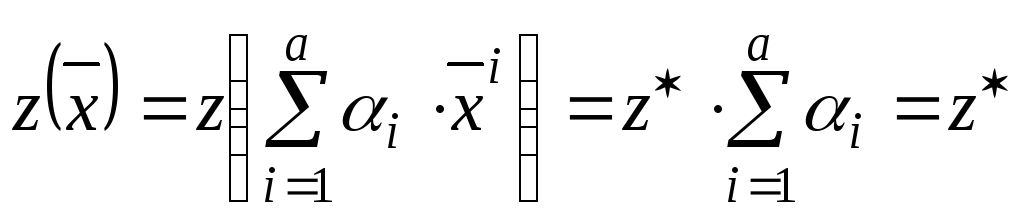. Тобто, якщо мінімальне значення досягається більш ніж в одній кутовій точці, то цього ж значення лінійна форма досягає в будь-якій точці, що є опуклою комбінацією цих точок

Теорема 2.2. Якщо відомо, що система векторів умов ,лінійно незалежна, причому така, що

,

де всі , то точкає кутовою точкою багатокутника розв’язків.

Теорема 2.3. Якщо вектор є кутовою точкою багатокутника розв’язків, то вектори умов, що відповідають додатним компонентам вектора, є лінійно незалежними. При цьому : кутова точка багатокутника розв’язків має не більш ніждодатних компонентів вектору; кожній кутовій точці багатокутника розв’язків відповідаєлінійно незалежних векторів, що належать системі векторів.

Підсумовуючи вище описане, можна відзначити такі властивості задач лінійного програмування:

1. Допустима множина розв’язків ЛП або порожня, або є опуклим багатокутником у Rⁿ, що є перетинанням півпросторів, які описуються нерівностями (2.2)-(2.3)). Вона може бути обмеженою, так і необмеженою; у будь-якому випадку це замкнений багатокутник.

2. Якщо допустима множина не порожня, а цільова функція обмежена зверху (для задачі максимізації, а для задачі мінімізації - обмежена знизу) на цій множині, то задача ЛП має оптимальне рішення.

3. Оптимальні розв’язки задачі ЛП (якщо вони існують) завжди знаходяться на границі припустимої множини. Точніше, якщо існує єдиний оптимальний розв’язок, то ним є одна з вершина багатокутника допустимих рішень.

4. Якщо дві або кілька вершин є оптимальними розв’язками, то будь-яка їх опукла комбінація також є оптимальним розв’язком, тобто існує нескінченна множина точок максимуму або мінімуму.

Методами розв’язання задач ЛП є графічний метод (у випадку двох змін­­них), або його різновиди (у загальному випадку).