8.5. Алгебраїчний метод розв’язання матричних ігор

Нехай задана матрична гра порядку 2 ^ 2, що описується матрицею

.

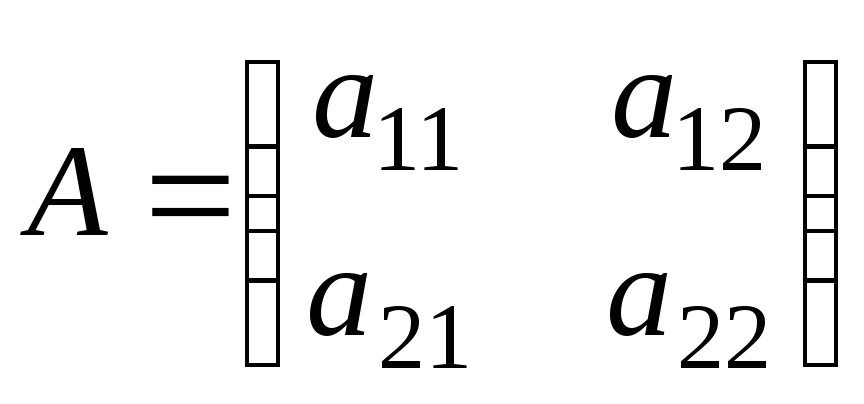Насамперед необхідно перевірити, чи є в даній грі сідлова точка. Якщо це так, то гра має розв’язок в чистих стратегіях, причому оптимальними стратегіями гравців 1 і 2 відповідно будуть чиста максмінна і чиста мінімаксна стратегії.

Якщо ж гра не має чистих стратегій, то обидва гравці мають тільки такі оптимальні стратегії, що використовують усі свої чисті стратегії з позитивними ймовірностями.

Інакше один із гравців (наприклад 1) має чисту оптимальну стратегію, а інший – тільки змішані. Не обмежуючи загальності, можна вважати, що оптимальною стратегією гравця 1 є вибір з ймовірністю 1 першого рядка. Далі, з властивості 8.1 випливає, що а₁₁ = а₁₂ =  і матриця має вигляд

.

Звідси легко побачити, що для матриць такого вигляду одна із стратегій гравця 2 є така, що домінує. Отже, за властивістю 2.4 цей гравець має чисту стратегію, що суперечить припущенню.

Нехай Х = (, 1  ) – змішана оптимальна стратегія гравця 1. Оскільки гравець 2 має змішану оптимальну стратегію, з властивості 2.1 отримаємо, що (див. також властивість 8.7)

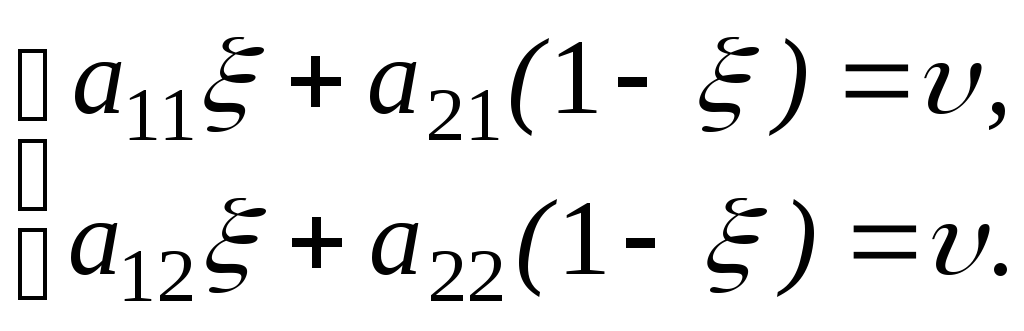
Звідси випливає, що при   0 стовпці матриці А не можуть бути пропорційними з коефіцієнтом, відмінним від одиниці. Якщо ж коефіцієнт пропорційності дорівнює одиниці, то матриця А приймає вигляд

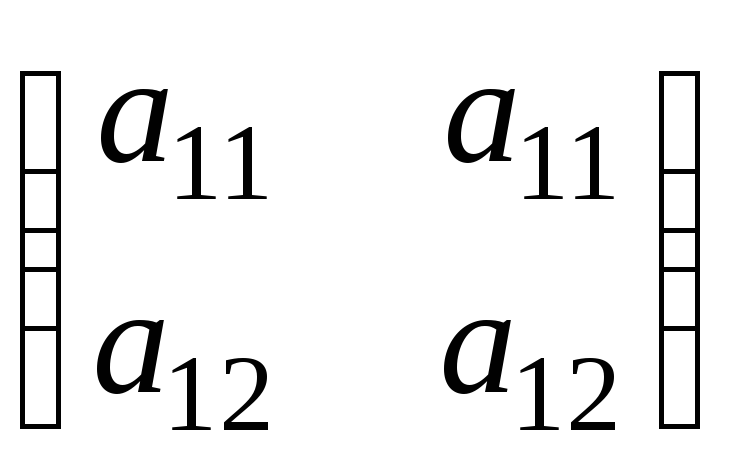
і гравець 1 має чисту оптимальну стратегію (він вибирає з ймовірністю 1 той з рядків, елементи якого не менше відповідних елементів іншого), що суперечить припущенню. Отже, якщо   0 і гравці мають тільки змішані оптимальні стратегії, то визначник матриці А відмінний від нуля. З цього випливає, що остання система рівнянь має єдиний розв’язок. Розв’язуючи цю систему, знаходимо

;

.

Аналогічні міркування приводять нас до того, що змішана оптимальна стратегія гравця 2 Y = (, 1 - ) задовольняє системі рівнянь

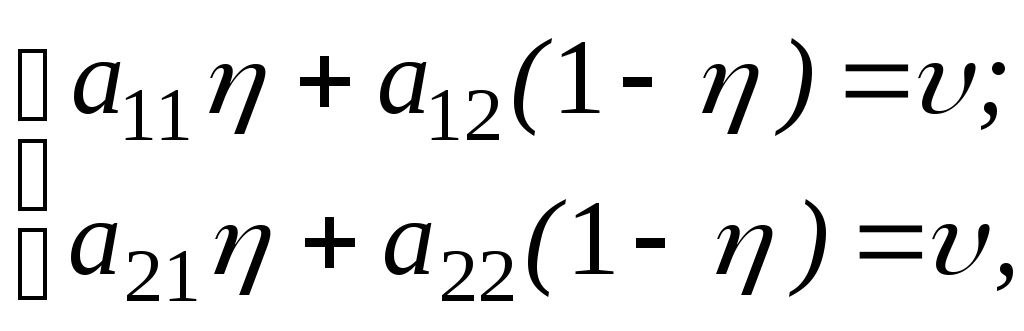
звідки

; .

Якщо ж платіжна матриця має розмірність т n, то для того щоб знайти розв’язок такої гри, треба відшукати такі невід’ємні x_i, i = 1,m, y_j, j = 1, n, які задовольняють співвідношення

Замінимо всі нерівності на рівності й спробуємо розв’язати отриману систему рівнянь. Якщо всі x_i , i= 1,m і y_j j= 1,n,то буде знайдено розв’язок гри. Інакше, якщо серед x_i чи y_j є хоч один не додатній елемент, це означає, що заміна всіх нерівностей рівностями не справедлива і треба тільки частину не­рівностей замінити рівностями і розв’язати ту саму систему. Пере­бираючи послідовно всі комбінації рівностей та нерівностей та роз­в'язуючи їх, відшукуємо розв’язок гри. При цьому слід мати на увазі, що якщо для будь-якого i= 1,m буде виконуватись нерівність

,

то x_i = 0.

Якщо ж для будь-якого j= 1,n буде

,

то y_j = 0.

Приклад 8.4. Розв’язжемо гру порядку 22, що описується матрицею

.

Оскільки у цій грі матриця сідлової точки немає, тому шукаємо розв'язок у змішаних стратегіях. ймовірності використання окремих чистих стра­тегій обчислюються за наведеними вище формулами:

при цьому, ціна гри визначиться як

,

а змішані стратегії гравців мають вигляд X^ =(5/6, 1/6),Y^ = (1/3, 2/3).

Приклад 8.5. Розв’яжемо гру порядку 22, що описується матрицею

.

Розглянемо випадок, коли всі нерівності замінено на рівності:

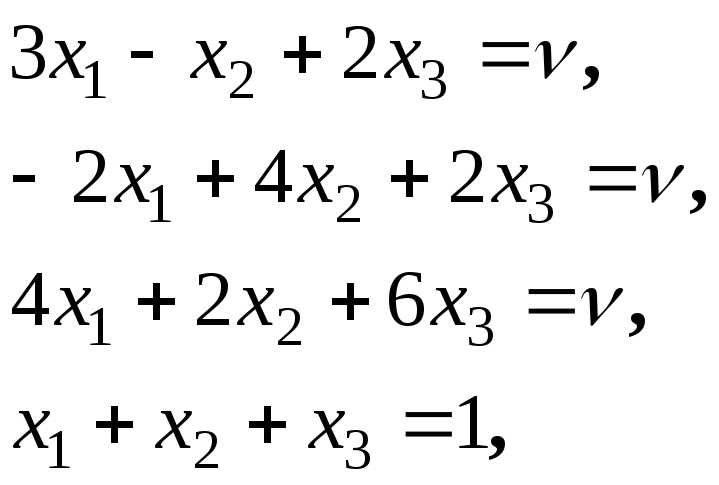
Ці рівняння не мають такого розв’язку, щоб ймовірності x_i та y_j були невід’ємні. Замінюючи рівності на нерівності, приходимо до такої системи:

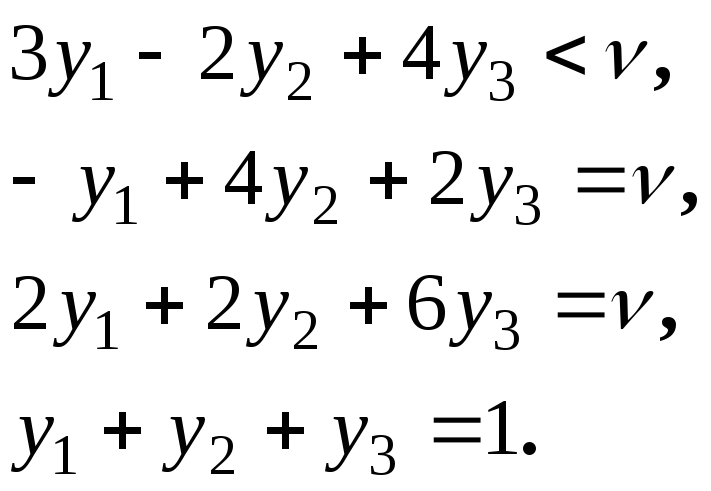
З нерівностей тавипливає, щоy₃ = 0 та x₁ = 0.

Тепер вже розв’яжемо таку систему рівнянь:

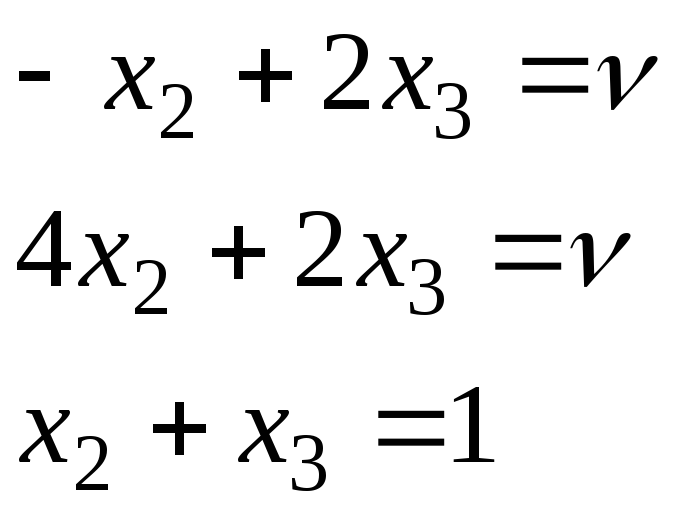
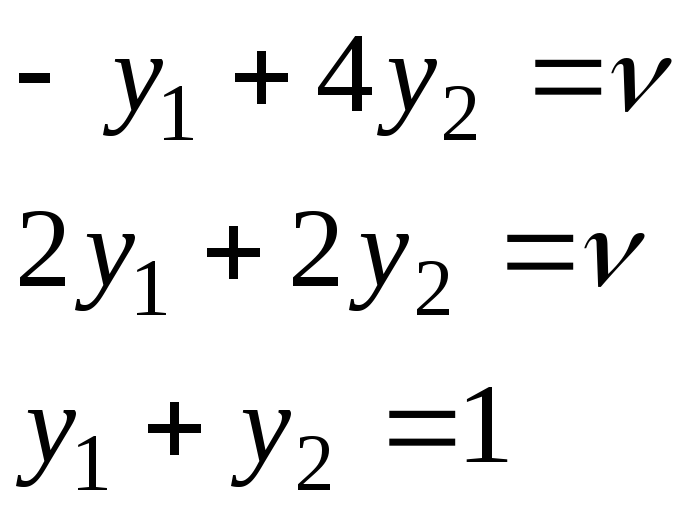
Вона має такий розв’язок: x₂ = 0, x₃ = 1, y₁ = 2/5, y₂ = 3/5,  = 2. Таким чином, ціна гри дорівнює 2, оптимальна змішана стратегія першого гравця Х* = (0, 0, 1), другого Y* =( 2/5,3/5,0 )