5.4 Методи оптимізації з використанням похідних

Доцільно припустити, що ефективність пошукових процедур істотно підвищиться, якщо на додаток до умови безперервності ввести вимогу диференціюємості цільової функції. Необхідна умова існування оптимуму цільової функції в точці x^*

W'(x^*) = d/dx  _x=x* = 0.

У випадку, якщо цільова функція містить члени, що включають x у третій і більш високих ступенях, то отримати аналітичний розв’язок рівняння W'(x) важко. У цих випадках доцільно використовувати чисельні методи знаходження коренів нелінійних рівнянь:

• метод середньої точки;

• метод хорд;

• метод дотичних;

Метод середньої точки. Метод заснований на алгоритмі виключення інтервалів, на кожній ітерації якого розглядається одна спробна точка R. Якщо в точці R виконується нерівність W'(R) < 0, то внаслідок унімодальності функції точка оптимуму не може лежати лівіше точки R. Аналогічно, якщо W'(R) > 0, то інтервал x >R можна виключити.

Нехай у інтервалі [a,b] існують дві точки N і P, у яких похідні W'(N) < 0 і W'(P) > 0. Оптимальна точка x^* розташована між N і P.

Крок 1. Покласти P = b, N = a, причому W'(a) < 0 і W'(b) > 0.

Крок 2. Обчислити R=(P+N)/2 і W'(R).

Крок 3. Якщо W'(R) <  , то закінчити пошук. Інакше, якщо W'(R) < 0, покласти N=R, і перейти до кроку 2. Якщо ж  W'(R) >  , покласти P = R і перейти до кроку 2.

Як випливає з логічної структури, процедура пошуку за методом середньої точки заснована на дослідженні тільки знаку похідної.

Приклад 5.6. Мінімізувати W(x)=2x²+(16/x) на інтервалі 1 x 5.

W'(x) = d(x)/dx = 4x - 16/x².

Ітерація 1.

Крок 1. N = 1, P = 5, W'(5) =19.36, W'(1) = -12.

Крок 2. R = (5+1)/2=3.

Крок 3. W'(3) = 10.22 > 0; покласти P = 3.

Ітерація 2.

Крок 2. R = (3+1)/2 = 2.

Крок 3. W'(2) = 4 > 0; покласти P = 2.

Ітерації продовжуються доти, поки не буде виконуватися нерівність

 W'(R),

 Метод хорд. Метод орієнтований на пошуку кореня рівняння W'(x) в інтервалі [a,b], у якому існують дві точки N і P, у яких знаки похідних різні. Алгоритм методу хорд дозволяє апроксимувати функцію W'(x) "хордою" і знайти точку, у якій січна графіку W'(x) перетинає вісь абсцис (див. на рисунку нижче).

Крок 1. Наступне наближення до стаціонарної точки x^* визначається за формулою .

Крок 2. Обчислити W'(R).

Крок 3. Якщо W'(R) <  , то закінчити пошук. Інакше необхідно вибрати одну з точок P або N, щоб знаки похідних у цій точці і точці R були різні. Повернутися до кроку 1.

Як видно з алгоритму, метод хорд реалізований на дослідженні як знаку похідної, так і її значення. Тому цей метод ефективніший, ніж метод середньої точки.

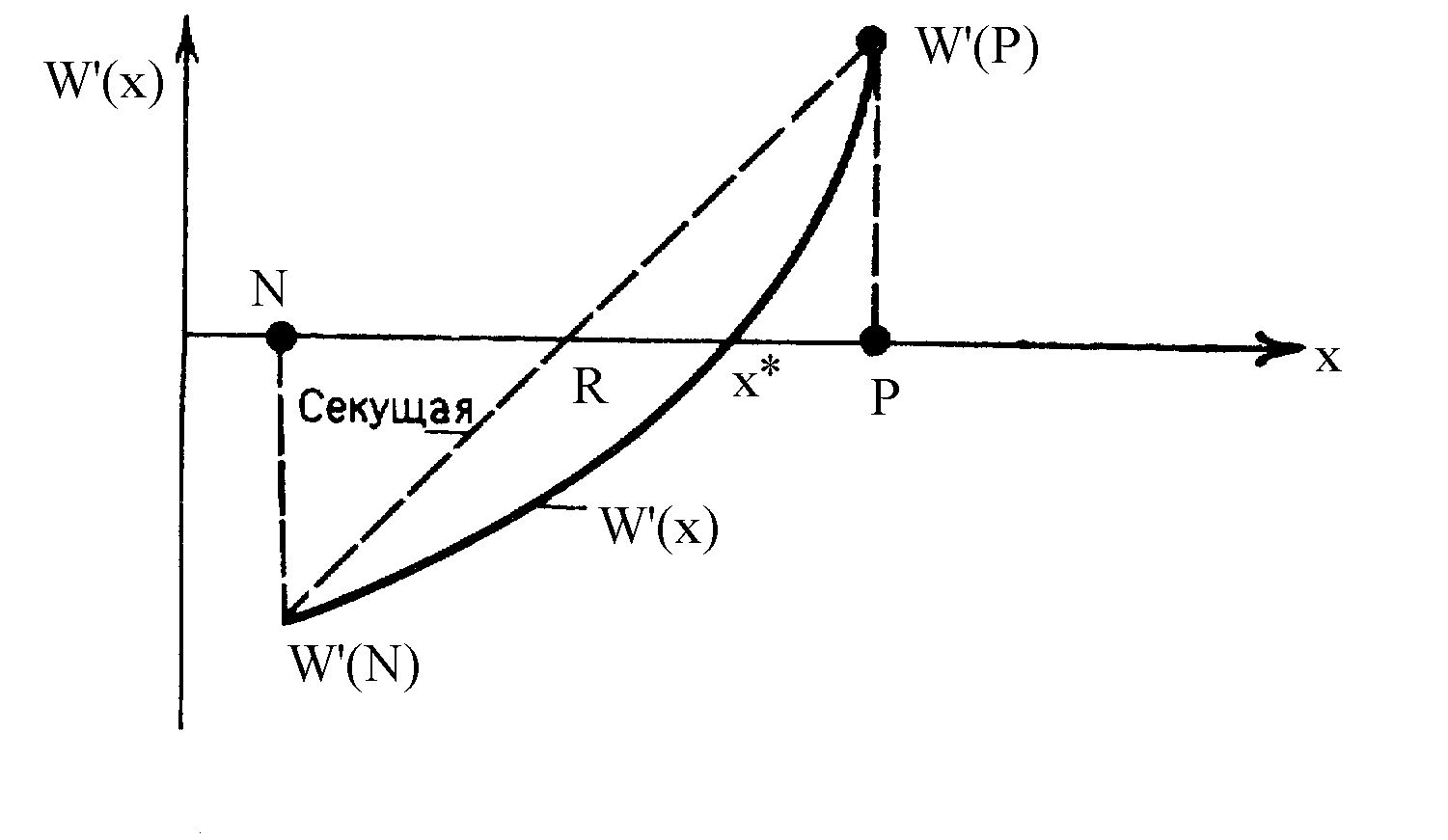
Приклад 5.7. Мінімізувати W(x)=2x²+(16/x) в інтервалі 1 x 5.

W'(x) = d(x)/dx = 4x - 16/x².

Ітерація 1.

Крок 1. N=1, P =5, W'(5)=19.36, W'(1) = -12.

Крок 2. R =5-{19.36/[(19.36+12)/4]}=2.53.

Крок 3. W'(2.53) = 7.62 > 0; покласти R = 2.53.

Ітерація 2.

Крок 2. R=2.53-{7.62/[(7.62+12)/1.53]}=1.94.

Крок 3. W'(1.94)=3.51>0; покласти R=1.94.

Ітерації продовжуються поки не буде виконуватись умова  W'(R)

Метод дотичних. Метод орієнтований на пошуку кореня рівняння W'(x) в інтервалі [a,b], у якому існують дві точки N і P, у яких знаки похідних різні. Робота алгоритму починається з точки x_o, що представляє початкове наближення кореня рівняння W'(x)=0. Далі будується лінійна апроксимація функції W'(x) у точці x₁, і точка, у якій апроксимуюча лінійна функція обертається в нуль, приймається як наступне наближення (див. на рисунку нижче). Якщо точка x_k прийнята як поточне наближення до оптимальної точки, то лінійна функція, що апроксимує функцію W'(x) у точці x_k, записується як W'(x, x_k) = W'(x_k) + W''(x_k)(x - x_k). Прирівнявши праву частину рівняння до нуля, одержимо наступне наближення до шуканої точки.

Крок 1. Наступне наближення до стаціонарної точки x^* визначається по формулі x_k+1 = x_k - [W'(x_k)/W''(x_k)].

Крок 2. Обчислити W'(x_k+1), W''(x_k+1)

Крок 3. Якщо  W'(x_k+1) <  , то закінчити пошук. Інакше необхідно повернутися до кроку 1.

Як видно з алгоритму, цільова функція W(x) повинна бути двічі диференційованою.

Приклад 5.8. Мінімізувати W(x)=2x²+(16/x), поклавши x₁=1.

W'(x) = d(x)/dx = 4x - 16/x², W"(x)= 4+(32/x³).

Ітерація 1. x₁=1, W'(1)=-12, W"(1)=36, x₂=1-(-12/36)=1.33

Ітерація 2. x₂=1.33, W'(1.33)=-3.73, W"(1.33)=17.6,

x₃ =1.33-(-3.76/17.6)=1.54

Ітерації продовжуються поки не буде виконуватись умова W'(x_k).