8.4 Властивості розв’язку матричних ігор

Позначимо через G (Х,Y,А) гру двох осіб з нульовою сумою, у якій гравець 1 вибирає стратегію х  Х , гравець 2 – y   , після чого гравець 1 отримує виграш А = А (х, y) за рахунок гравця 2.

Означення 8.6. Стратегія х¹ гравця 1 домінує (строго домінує) над стратегією х², якщо

А (х¹, y)  А (х², y) (А (х¹, y) > А (х², y)), y  .

Стратегія y¹ гравця 2 домінує (строго домінує) над стратегією y², якщо

А (х, y¹)  А (х, y²) (А (х, y¹) < А (х, y²)), х  Х.

При цьому стратегії х² і y² називаються домінуємими (строго).

Спектром змішаної стратегії гравця у скінченій антагоністичній грі називається множина усіх його чистих стратегій, ймовірність яких відповідно до цієї стратегії позитивна.

Властивість 8.1. Якщо чиста стратегія одного з гравців знаходиться в спектрі деякої його оптимальної стратегії, то виграш цього гравця в ситуації, утвореною даною чистою стратегією і будь-якою оптимальною стратегією іншого гравця, дорівнює значенню скінченої антагоністичної гри.

Властивість 8.2. Жодна строго домінуєма чиста стратегія гравця не знаходиться в спектрі його оптимальної стратегії.

Гра G = (Х,Y,А) називається підгрою гри G (Х, Y, А), якщо Х  Х,  , а матриця А є підматрицею матриці А. Матриця А при цьому будується такий чином. В матриці А залишаються рядки і стовпці, що відповідають стратегіям Х і , а інші “викреслюються”. Усі ті що залишиться після цього в матриці А і будуть утворювати матрицю А.

Властивість 8.3. Нехай G = (Х,Y,А) – скінчена антагоністична гра, а G= (Х \ х,Y,А) – підгра гри G, а х – чиста стратегія гравця 1 у грі G, що домінується деякою стратегією , і спектр якої не міститьх. Тоді будь-який розв’язок (х^о, y^о, ) гри G є розв’язком гри G.

Властивість 8.4. Нехай G = (Х,Y,А) – скінчена антагоністична гра, а G= (Х,Y \ y,А) – підгра гри G, а y – чиста стратегія гравця 2 у грі G, що домінується деякою стратегією , і спектр якої не міститьy. Тоді будь-який розв’язок гри G є розв’язком G.

Властивість 8.5. Якщо для чистої стратегії х гравця 1 виконуються умови властивості 2.3, а для чистої стратегії y гравця 2 виконуються умови властивості 2.4, то будь-який розв’язок гри G = (Х \ х,Y \ y,А) є розв’язком гри G = (Х,Y,А).

Властивість 8.6. Трійка (х^о, y^о, ) є розв’язком гри G = (Х,Y,А) тоді і тільки тоді, коли (х^о, y^о, k +а) є розв’язком гри G(Х,Y,кА+а), де а – будь-яке дійсне число, k > 0.

Властивість 8.7. Для того, щоб х^о = () була оптимальною змішаною стратегією матричної гри з матрицею А і ціною гри , необхідно і достатньо виконання таких нерівностей:

, (j = ). (8.4)

Для того щоб y^о = (, ...,, ...,) була оптимальною змішаною стратегією гравця 2 необхідно і достатньо виконання нерівностей:

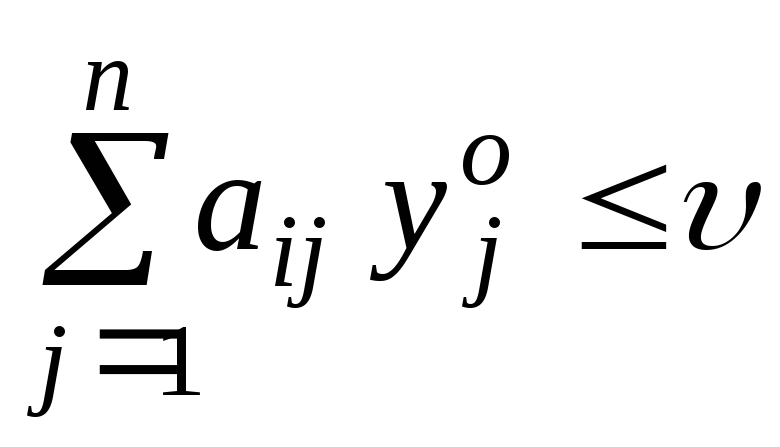, (i = ). (8.5)

З останньої властивості випливає: щоб встановити, чи є передбачувані (х, y) і  розв’язком матричної гри, досить перевірити, чи задовольняють вони нерівностям (8.4) і (8.5). З іншого боку, знайшовши ненегативні розв’язки нерівностей (8.4) і (8.5) спільно з рівняннями

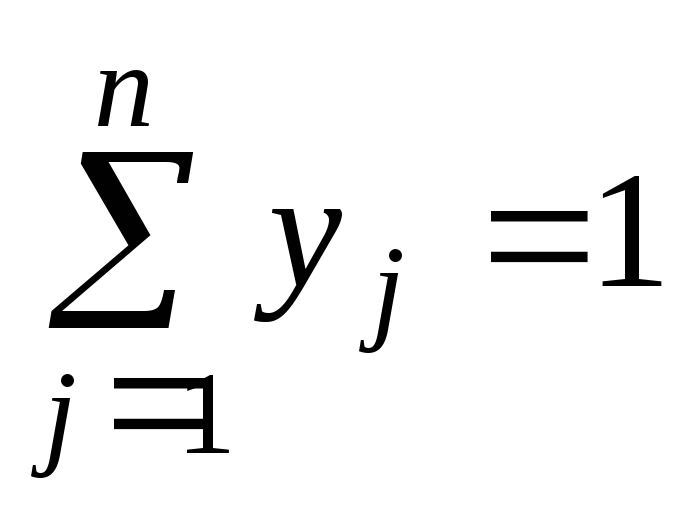, (8.6)

отримаємо розв’язок матричної гри.

Таким чином, розв’язок матричної гри зводиться до пошуку ненегативних параметрів розв’язань лінійних нерівностей (8.4) (8.5) і лінійних рівнянь (8.6). Однак це вимагає великого обсягу обчислень, який зростає зі збільшенням числа чистих стратегій гравців.

Наприклад для матриці 33 маємо систему з 6 нерівностей і 2 рівнянь. Тому, по перше, слід, використовуючи властивості 8.2 і 8.3, зменшити по можливості, число чистих стратегій. А по-друге, в усіх випадках перевірити виконання рівності

= .

Якщо ця рівність виконується, то обидва гравці мають чисті оптимальні стратегії (гравець 1 ( чисту максмінну, а гравець 2 ( чисту мінімаксну). Інакше хоча б в одного гравця оптимальні стратегії будуть змішані. Для матричних ігор невеликого розміру ці розв’язки можна знайти, застосовуючи властивості 8.1 – 8.5.

Зауваження. Слід відзначити, що виключення не строго домінуємих стратегій може призвести до втрати деяких розв’язків. Якщо ж виключаються тільки строго домінуємих стратегій, то множина розв’язків гри не зміниться.

Приклад 8.3. Нехай G = (Х,Y,А), де Х = {1, 2, 3, 4}; Y = {1, 2, 3, 4}, а функція виграшу А задана таким чином:

де C > 0.

Розв’язання. Насамперед відзначимо, що за властивістю 8.6 досить розв’язати гру G¹ = (Х,Y,А), де А¹ = А1/C . У матричній формі гра G¹ визначається матрицею виграшів

.

Елементи четвертого рядка цієї матриці “  ” відповідних елементів третього рядка, а тому третя стратегія гравця 1 домінує над четвертою. Крім того, елементи першого стовпця матриці А¹ “  ” відповідних елементів другого стовпця, Отже, друга стратегія гравця 2 домінує над його першою стратегією.

Далі, із властивості 2.5 випливає, що будь-який розв’язок гри G² = (Х \ {4}, Y \ {1}, А¹) є розв’язком гри G¹. У матричній формі гру G² можна описати матрицею

.

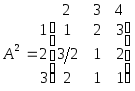Очевидно, що елементи другого рядка “ ” напівсуми відповідних елементів першого і третього рядків. Крім того, елементи третього стовпця матриці А² “ “ відповідних елементів другого стовпця. Застосовуючи властивість 2.5 одержимо, що будь-який розв’язок гри G³ = (Х \ {4,2}, Y \ {1,4}, А²), тобто

.

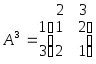є розв’язком гри G², а отже і гри G¹.

Матриця А³ не має сідлової точки, тому що не виконується рівність

= ,

і, значить, гра G³ не має розв’язку в чистих стратегіях, тобто оптимальні стратегії гравців є змішаними. Ці стратегії, у даному випадку, легко знайти з аналізу структури матриці А³. Оскільки матриця А³ симетрична, можна припустити, що гравці в оптимальній стратегії використовують свої чисті стратегії з рівними ймовірностями.

Дійсно, якщо гравець 1 вибирає з рівними ймовірностями стратегії 1 і 3, то під час застосування кожної з двох чистих стратегій гравцем 2 математичне очікування виграшу гравця 1 буде рівним

, або .

Аналогічно, якщо гравець 2 використовує свої чисті стратегії 2 і 3 з рівними ймовірностями, то математичне очікування його програшу буде дорівнювати 3/2. Отже, зазначені стратегії є оптимальними в грі G³, а величини 3/2 – значенням гри G³. З попереднього випливає, що ці стратегії оптимальні, також, і у грі G¹.

Таким чином, стратегія Х = (1/2 , 0, 1/2, 0) є оптимальною стратегією гравця 1, стратегія Y = (0, 1/2, 1/2, 0) – оптимальною стратегією гравця 2 у грі G¹, а значення гри G¹ дорівнює 3/2. У силу властивості 2.4 розв’язком гри G буде трійка (Х, Y, 3С/2 ).