6.3. Метод Франка – Вулфа розв’язання задач квадратичного програмування (зкп)

У матричній формі ЗКП можна записати у вигляді

де D - симетрична, від’ємно визначена квадратна матриця коефіцеєнтів квадратичної форми.

Як відомо, із умов теореми Куна-Таккера випливає, що вектор X* буде розв'язком ЗКП тоді й тільки тоді, коли існують такі m-вимірні вектори  0 та W  0 і n-вимірний вектор V=0, за яких виконуються умови:

C+DX–A+V=0; b–AX–W=0; V^TX=0; W^T=0.

Дві останні умови нелінійні (умови доповняльної нежорсткості). З них випливає, що меншою мірою n змінних з Х та V , а також m змінних з  та W мають обертатися у нуль. Звідси випливає, що для знаходження розв'язку ЗКП з від’ємно визначеною квадратичною формою досить розв’язати систему рівнянь і задовольнити умови доповняльної нежорсткості.

Використовуючи метод штучного базису, формулюємо задачу:

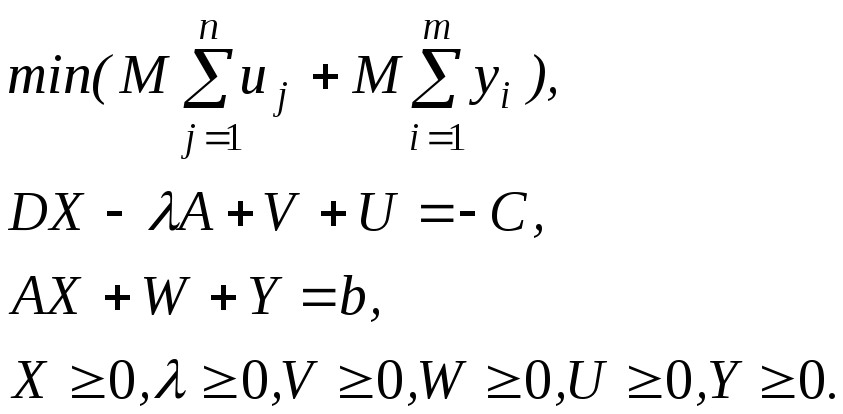
Якщо у результаті її розв'язання вдалось вивести з базису усі штучні змінні і виконати умови доповняльної нежорсткості, то знайде­ний базис­ний розв'язок буде розв'язком ЗКП. Розглянемо метод Франка - Вулфа.

Переформулюємо задачу: серед довільних базисних розв'язків системи знайти такий, який обертає у нуль V^TX+^W. Розглянемо вектор

Z=(x₁,…,x_n, ₁,…,_m, v₁,…,v_n, w₁,…,w_m)

та вектор =(v₁,…,v_n, w₁,…,w_m, x₁,…,x_n, ₁,…,_m).

Тоді

V^TX+W^T =Z^T min,

BZ=d,

Z  0.

де

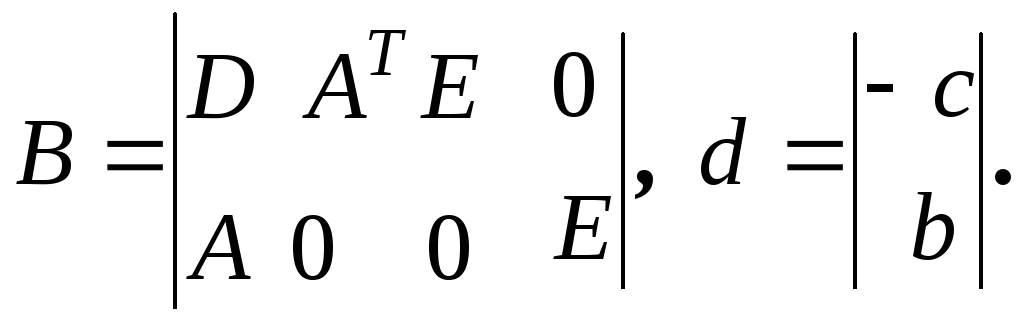
Виконуємо ряд ітерацій так, щоб опукла функція T(Z) = Z^TZ мінімізувалася за таким рекурентним правилом: у результаті к-го кроку маємо довільний розв'язок Z^k, що відповідає системі обмежень задачі, а також довільний розв'язок ^k, який задовольняє тим самим обмеженням, але не обов'язково буде базисним. Йому відповідає до­датне значення T(Z) (на першому кроці ^^). Починаючи з базисного розв'язку Z^k , мінімізуємо лінійну відносно Z форму (Z^k )^T^ . Маємо послідовність базисних розв'язків Z⁰=Z^k, Z¹, Z² , ... , причому (Z⁰)^T^ > (Z¹)^T^ . Обчислення закінчується, якщо

а) (Z^h)^Th =0;

б) (Z^h)^T^k  (^k)^Tk.

У випадку а) Z^k - розв’язок ЗКП, а у випадку б) знаходимо

Z^k+1=Z^k; ^k+1=^k+(Z^k+1–^k),

=min

На кожному кроці маємо або а) або б) однак через певну кількість кроків будемо мати тільки а).

Приклад 6.3. Розв’язати ЗКП методом Франка – Вульфа:

10x₁+20x₂–2x₁²–2x₂²+x₁x₂ max,

x₁+x₂  10,

x₂  4,

x₁  0, x₂  0.

Матриця D має вигляд

D =

Оскільки знаки її мінорів змінюються спочатку “ - ” потім “ +” то згідно з критерієм Сильвестра цільова функція буде угнутою.

Запишемо функцію Лагранжа квадратичної задачі

L(X,)=10x₁+20x₂–2x₁²–2x₂²+x₁x₂+₁(10–x₁–x₂)+₂(4–x₂).

Умови теореми Куна – Таккера мають вигляд:

1. 2.

= 10– 4x₁+ x₂–  ₁  0 ; x₁ = x₁ (10– 4x₁+ x₂–  ₁) = 0 ;

= 20– 4x₂–  ₁– ₂  0; x₂ = x₂ (20– 4x₂–  ₁– ₂ ) = 0;

= 10 – x₁– x₂  0; ₁ = ₁ (10– x₁– x₂ ) = 0;

= 4 – x₂  0; ₂ = ₂ (4– x₂ ) = 0 .

Треба знайти такий розв’язок системи умов 1, який одночасно задовольнив би і систему 2. Перепишемо систему 1 у вигляді:

4x₁–x₂+₁  10 ,

–x₁+4x₂+₁+₂  20 ,

x₁+x₂  10,

x₂  4 .

Вводячи у цю систему обмежень невід’ємні додаткові змінні V₁, V₂, W_!, W₂ дістаємо

4x₁– x₂+ ₁– V₁ = 10 ,

–x₁+ 4x₂+₁+ ₂– V₂ = 20 ,

x₁+ x₂ + W₁ = 10,

x₂ + W₂ = 4 .

При цьому мають виконуватись умови доповняльної нежорстокості

x₁V₁ = 0, x₂V₂ = 0, ₁W₁ = 0, ₂W₂ = 0.

Запишемо вектор Z = (z₁ , z₂ , z₃ , z₄ , z_­5 , z₆ , z₇ , z₈), як

Z=(x₁,x₂, ₁, ₂, v₁, v₂, W₁, W₂)

та вектор у вигляді

.

Далі запишемо V^TX+W^T=Z^T/2.

Тепер задачу можна зобразити у вигляді

Z^Tmin ;

BZ = d ;

Z  0 ,

де

4 –1 1 0 –1 0 0 0 10

B = –1 4 1 1 0 –1 0 0 , d = 20 .

1 1 0 0 0 0 1 0 10

0 1 0 0 0 0 0 1 4

Для знаходження довільного базисного розв’язку використаємо метод штучних змінних. Введемо в систему обмежень штучну змінну U₁=Z_g і запишемо цільову функцію L^’ =Mz_g min і початкову симплекс-таблицю у вигляді табл. 6.1.

Таблиця 6.1

i	Б	С	Z1	0	0	0	0	0	0	0	0
				z1	z2	z3	z4	z5	z6	Z7	z8
1	z9	M	10	4	-1	1	0	-1	0	0	0
2	z4	0	20	-1	4	1	1	0	-1	0	0
3	z7	0	10	1	1	0	0	0	0	1	0
4	z8	0	4	0	1	0	0	0	0	0	1
m+2			10	4	-1	1	0	-1	0	0	0

Зробимо крок симплексних перетворень і дістанемо табл. 6.2.

Таблиця 6.2

i	Б	С	Z2	0	0	0	0	0	0	0	0
				z1	z2	z3	z4	z5	z6	z7	z8
1	z1	0	5/2	1	-1/4	1/4	0	-1/4	0	0	0
2	z4	0	45/2	0	15/4	5/4	1	-1/4	-1	0	0
3	z7	0	15/2	0	5/4	0	0	1/4	0	1	0
4	z8	0	4	0	1	0	0	0	0	0	1
m+2		0	0	0	0	0	0	0	0	0	0

Для перeвірки умов доповняльної нежорстокості розглянемо вектори

Z² = =

Оскільки (Z²)^TZ²  0 то разом з табл. 6.2 знайшли довільний розв’язок ^Z⁰=Z⁰. Починаючи з нього мінімізуємо лінійну щодо Z функцію:

Табл. 6.3 випливає безпосередньо з табл. 6.2.

Таблиця 6.3

I	Б	С	Z1	0	0	15/2	4	5/2	0	0	45/2
				z1	z2	z3	z4	z5	z6	z7	z8
1	z1	0	5/2	1	-1/4	1/4	0	-1/4	0	0	0
2	z4	4	45/2	0	15/4	5/4	1	-1/4	-1	0	0
3	z7	0	15/2	0	5/4	0	0	1/4	0	1	0
4	z8	45/2	4	0	1	0	0	0	0	0	1
m+1			i	Б	С	Z0	0	-7/2	-4	0	0

Вибравши другий стовпець і четвертий рядок ведучими, робимо крок симплексного виключення і переходимо до нової таблиці 6.4

Таблиця 6.4

I	Б	С	Z1	0	0	15/2	4	5/2	0	0	45/2
				z1	z2	z3	z4	z5	Z6	Z7	z8
1	z1	0	7/2
2	z4	4	15/2
3	z7	0	5/2
4	z2	0	4
m+1			30

Оскільки то перевіряємо умови доповняльної не жорсткості

= =

Вони виконуються оскільки (Z¹)^TZ¹ = 0. Таким чином знайдемо оптимальний розв’язок ЗКП

X^* = ;

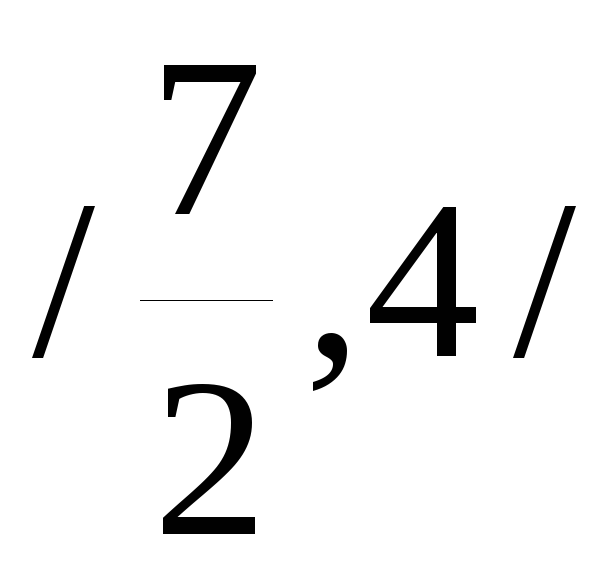F(X^*) = 62,5 .