4.4 Задача частково дискретного лп. Метод Дальтона-Ллевелiна

Постановка частково дискретної задачі лінійного програмування (ЧДЗЛП). Знайти вектор x=(x₁,...,x_n), що мiнiмiзує цільову функцію

L(x) = c₁x₁ + ... + c_nx_n (4.16)

i задовольняє систему обмежень

a₁₁x₁ + . . . + a_1nx_n = a₁₀,

. . . . . . . . . . . . . . . . . . . . . . . , (4.17)

a_m1x₁ + . . . + a_mnx_n = a_m0,

x_j³0, j=1,...,n, (4.18)

x_jÎ{X_j1,...,X_j,nj}, j=1,...,p, (p£n), (4.19)

де 0 = X_j1 <...< X_j,nj.

Виклад методу Дальтона-Ллевелiна. Метод Дальтона-Ллевелiна, як i методи Гоморi, є одним з методів відсікання i полягає у такому.

Розв'язується допоміжна ЗЛП (4.16)–(4.18), яку отримують з вихідної задачі (4.16)–(4.19) відкиданням умови дискретності змінних (4.19). Якщо її розв'язок задовольняє умову (4.19), то він i є розв'язком вихідної ЧДЗЛП. Інакше, від розв'язаної ЗЛП переходять до нової допоміжної ЗЛП приєднанням лінійного обмеження, що задовольняє дискретні (в розумінні умов (4.19)) розв'язки вихідної ЧДЗЛП, але не задовольняє отриманий розв'язок вихідної ЗЛП. Це додаткове обмеження визначає деяку площину, що відсікає, i називається правильним вiдсіканням. Приєднання нових правильних вiдсікань до початкової ЗЛП здійснюється до тих пір, поки на деякому кроцi не буде отриманий дискретний розв'язок допоміжної ЗЛП, який, як очевидно, буде оптимальним розв'язком вихідної ЧДЗЛП.

В методі Дальтона-Ллевелiна правильне вiдсікання будується таким чином. Нехай на останній iтерацiї симплекс-методу під час розв'язування допоміжної ЗЛП її непрямі обмеження набули вигляду:

x_i + Q_i,m+1 x_m+1 +...+ Q_in x_n = Q_i0, i=1,...,m,

i розв'язком допоміжної ЗЛП є вектор x = (Q₁₀,...,Q_m0, 0,...,0).

Нехай існує номер r (r£p) такий, що Q_r0 не задовольняє (4.19), до того ж X_rt < Q_r0 < X_r,t+1 для деякого t=1,...,n_r1. Тоді правильне вiдсікання методу Дальтона-Ллевелiна має вигляд:

x_n+1 – D_r,m+1 x_m+1 –...– D_rn x_n = –(Q_r0 – X_rt), (4.20)

де x_n+1 ³ 0 — додаткова змінна,

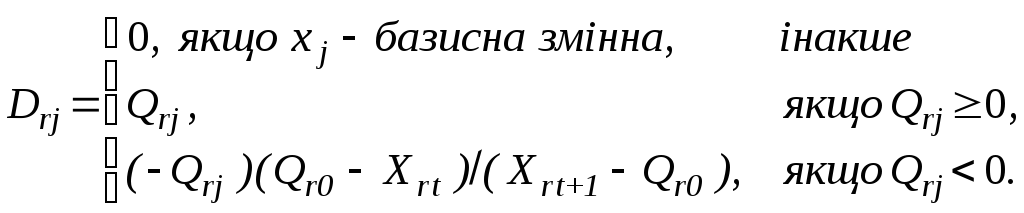^(4.21)

Алгоритм методу Дальтона-Ллевелiна.

1. Розв'язуємо допоміжну ЗЛП (4.16)–(4.18). Нехай x(0) – її оптимальний розв'язок. Якщо ця задача не має розв'язку, то вихідна ЧДЗЛП також не має розв'язку.

2. Нехай на s-й iтерацiї розв'язана допоміжна ЗЛП, що має M обмежень та N змінних, x(s) – її оптимальний розв'язок.

Припустимо, що x(s) визначається за канонічними обмеженнями останньої iтерацiї, а саме:

x_i + Q_i,M+1 x_M+1 +...+ Q_iN x_N = Q_i0, i=1,...,M,

звідки випливає, що x(s) = (Q₁₀,...,Q_M0, 0,...,0).

3. Якщо Q_i0 (i=1,...,p) задовольняє умову (4.19), то кінець: x(s) є розв'язком вихідної ЧДЗЛП. Інакше,

4. Знаходимо r=min{i} по всіх i (i=1,...,p) таких, що для деякого t (t=1,...,n_i1) X_it<Q_i0<X_i,t+1, i будуємо додаткове обмеження за формулами (4.20)–(4.21) при m=M та n=N.

5. Розширюємо таблицю за рахунок (M+1)-го рядка (додаткове обмеження) та (N+1)-го стовпця, що відповідає додатковій змінній x_N+1.

6. Розв'язуємо розширену ЗЛП за допомогою двоїстого симплекс-ме­тоду (ДСМ) i переходимо до пункту 2 із заміною s на s+1, M на M+1, N на N+1. Якщо на деякій iтерацiї ДСМ одна з додаткових змінних задачі знову стає базисною, то з подальшого розгляду виключаються відповідні їй рядок та стовпець i під час переходу до пункту 2 замінюється лише s на s+1.