Міністерство освіти і науки України

Бердичівський коледж промисловості, економіки та права

Волошина З. П.

Методична розробка

з дисципліни « Вища математика»

на тему: «Диференціальні рівняння»

для студентів другого курсу спеціальності 5.05050302

« Технологія обробки матеріалів на верстатах і

автоматичних лініях»

Бердичів 2010

Автор-укладач З.П. Волошина

Методична розробка з дисципліни « Вища математика» на тему: « Диференціальні рівняння»

У даній методичній розробці викладено, на доступному рівні, в логічній послідовності, матеріал щодо вивчення диференціальних рівнянь.

В розробці подано загальні відомості про диференціальні рівняння: задачі, що приводять до дифрівнянь, порядок, частинний і загальний розв'язки диференціального рівняння, задачу Коші; матеріал про рівняння з відокремленими змінними і рівняння із змінними, що відокремлюються; розглянуто однорідні рівняння та лінійні рівняння першого порядку.

До кожного типу диференціальних рівнянь наведено приклади розв’язування, з детальними кроками розв'язку.

В кінці розробки вказано використану літературу.

Розробка розрахована для студентів другого курсу спеціальності «Технологія обробки матеріалів на верстатах і автоматичних лініях» та студентів заочного відділення.

Розглянуто на засіданні циклової комісії

фізико-хіміко-математичних дисциплін

Протокол № від 2010р.

Голова циклової комісії:

О.О.Горленко.

Диференціальне рівняння кривої, яка в кожній точці має задану дотичну

Нехай G – деяка множина точок М площини, на якій введена прямокутна система координат, і нехай х, у – координати точок М. Так як між точками площини і парами чисел (х;у) є взаємно однозначну відповідність, тоді говорять, що G множина точок (х;у).

Якщо кожній точці (х;у) з множини G ставиться у відповідність деяке дійсне число f(x;y), тоді f називається функцією точки (х;у) або функцією двох змінних х, у, яка визначена на множині G і позначається f(x;y), (x;y) G.

Розглянемо тепер наступну задачу.

Знайти рівняння кривої, яка в кожній своїй точці з координатами х, у має дотичну з заданим кутовим коефіцієнтом .

Іншими словами, потрібно знайти функцію , яка задовольняє рівнянню

(1)

де - похідна по х від шуканої функції.

Це рівняння називається диференціальним рівнянням,

функція φ(х) – його розв'язком ,

а крива, задана рівнянням - інтегральною кривою.

Розглянемо один випадок.

Нехай функція f залежить тільки від х і визначена на деякому інтервалі(а;b). Рівняння

(2)

розв'язується в теорії невизначених інтегралів. Було показано, що всі розв'язки цього рівняння задаються формулою

Ця формула містить неявно довільну сталу С.

Дійсно, якщо F(x) – деяка первісна функції f(x), то

(3)

Таким чином, рівняння (2) має нескінченну множину розв'язків . Будь-яка крива, задана рівнянням (3) при фіксованому С, являється розв’язком поставленої задачі.

З теорії визначених інтегралів відомо, що у будь-якої неперервної функції f(x) є деяка первісна і цією первісною являється інтеграл із змінною верхньою межею. Звідси

.

Крива,що задана цим рівнянням, проходить через точку з координатами х₀, С. Звідси, через кожну точку (х₀;у₀), де х₀ (а;b), проходить єдина інтегральна крива

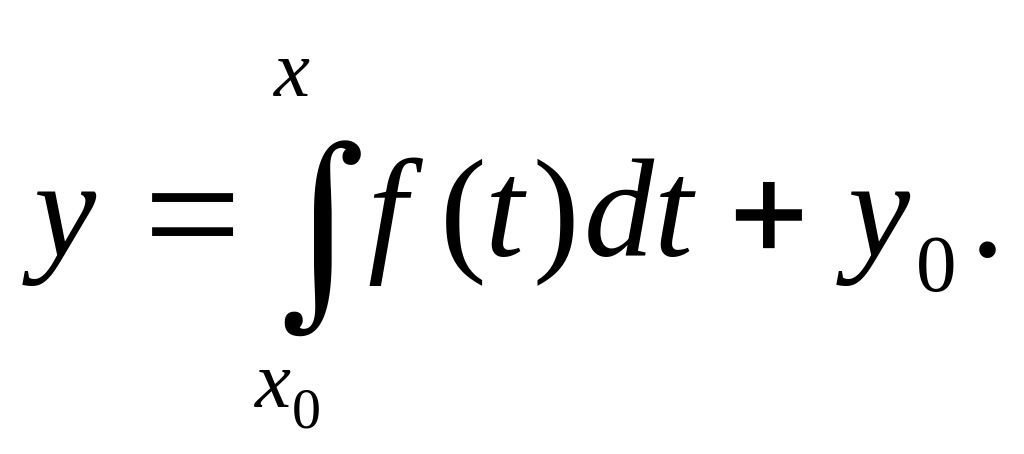
Загальні поняття та означення

Означення: Рівняння, що містить незалежну змінну, функцію, її похідні або диференціали називається диференціальним рівнянням.

Наприклад, x dy=2y dx або у' = 4х , ,

Означення: Найвищий порядок похідної, що входить в рівняння називається порядком рівняння.

Означення: Розв'язком диференціального рівняння називається функція при підстановці якої в рівняння воно перетворюється в правильну рівність.

Означення: Рівняння, які мають похідні або диференціали не вище першого порядку, називаються диференціальним рівнянням першого порядку.

Розв'язки бувають загальний і частинний.

Означення: Розв'язок диференціального рівняння в якому кількість сталих дорівнює порядку рівняння називається загальним розв'язком диференціального рівняння.

Означення: Розв'язок диференціального рівняння при конкретних значеннях сталих називається частинним розв'язком диференціального рівняння.

Означення: Задача на знаходження частинного розв'язку, що задовольняє початковим умовам, називається задачею Коші.

Диференціальні рівняння мають велике використання в геометрії, механіці, фізиці та інших дисциплінах, а також в техніці.

Задачі, що приводять до диференціального рівняння

Скласти рівняння кривої, що проходить через точку М(-1;4), якщо кутовий коефіцієнт дотичної, проведеної в будь якій точці, дорівнює

Розв'язок

Виходячи з геометричного змісту похідної

За умовою ,

підставимо в рівняння і одержимо

.

Це рівняння називається диференціальним. Розв'яжемо його:

Розпишемо похідну, як відношення диференціалів

, домножимо рівність на , одержимо

Знайдемо інтеграл від лівої і правої частини рівняння:

- загальний розв'язок.

Розв'яжемо задачу Коші.

Так як за умовою крива проходить через точку М(-1;4) , то .

Підставимо в загальний розв'язок і та знайдемо значення сталої С

- частинний розв'язок.

Отже, рівняння кривої, що проходить через точку М(-1;4) має вигляд

Відповідь: рівняння кривої .