Диференціальні рівняння з відокремленими змінними

Означення: Диференціальні рівняння вигляду

M(x) dx +N(y)dy=0 (1)

називаються диференціальними рівняннями з відокремленими змінними.

Загальний розв’язок диференціального рівняння має вигляд

∫M(x)dx + ∫N(y)dy=C (2)

і розв’язок задачі Коші з початковими умовами х = х₀, у = у₀ має вигляд

(3)

Диференціальні рівняння з відокремленими змінними зводяться до знаходження інтегралів.

Приклад 1:

Знайти загальний розв’язок диференціального рівняння

Розв'язування

Це є рівняння з відокремленими змінними

Загальний розв’язок диференціального рівняння має вигляд

Інтегруючи, одержимо

Відповідь:

Приклад 2 . Розв'язати рівняння

Розв'язування

Це є рівняння з відокремленими змінними

Змінні тут розділені. Інтегруючи, отримаємо

отримаємо

або

Так як С довільна величина, то можна позначити 2С через , взявши до уваги, що ліва частина рівності додатня.

Тоді рівняння прийме вигляд:

Це і є загальний розв'язок або, як говорять, загальний інтеграл даного диференціального рівняння.

З геометричної точки зору ми отримали сімейство (сукупність) концентричних кіл з центром в початку координат і радіусом, рівним С.

(Зрівняйте отримане рівняння з відомим рівнянням кола вигляду:

Відповідь:

Приклад 3. Розв'язати рівняння

Розв'язування

Змінні тут розділені. Інтегруючи, отримаємо:

отримаємо:

або

довільну змінну С можна позначити через

тоді

Подамо в правій частині рівняння суму логарифмів в вигляді логарифма добутку

звідки

Це і є загальний інтеграл даного диференціального рівняння.

З геометричної точки зору ми отримали рівняння сукупності прямих, центром яких є точка М(1;-1) з кутовим коефіцієнтом С.

Відповідь:

Диференціальні рівняння першого порядку з

відокремлювальними змінними

Якщо кожна частина диференціального рівняння являє собою добуток деякого виразу, залежного від однієї змінної, на диференціал цієї змінної, то говорять, що змінні у рівнянні відокремлені;

наприклад, x dx = y dy.

В цьому випадку рівняння можна інтегрувати почленно.

Означення: Рівняння, в яких змінні розділяються, називаються диференціальним рівнянням з відокремлювальними змінними.

Для того щоб розв'язати диференціальне рівняння з відокремлювальними змінними, потрібно відокремити змінні, а потім взяти інтеграл від обох частин рівняння.

Розглянемо декілька прикладів.

Приклад 4 . Розв'язати диференціальне рівняння x dy = y dx

Знайти загальний і частинний розв'язки, якщо при х=5 , у =10.

Розв'язування

Це рівняння з відокремлювальними змінними.

Для відокремлення змінних обидві частини рівняння поділимо на вираз ху, одержимо:

.

Інтегруючи обидві частини останнього рівняння, знайдемо

,

або

ln│y│=ln│x│+ln │C│.

(В правій частині стале C подамо у вигляді ln │C│ для зручності потенціюваня. ) Потенціюючи рівність, отримаємо:

│у│=│Cx│,

або у = ± Сх.

Одержали загальний розв'язок рівняння в вигляді

y = Сх

(знаки ± можна опустити, оскільки С довільна стала).

Для знаходження частинного розв'язку рівняння знайдемо значення сталого С, підставивши в одержане рівняння початкові умови: х=5 та у=10

10 = 5С,

звідси

С=2.

Отже,

y =2х. - частинний розв'язок.

Відповідь: y = Сх - загальний розв'язок рівняння;

y =2х. - частинний розв'язок.

Приклад 5. Розв'язати рівняння , якщо при х=0 , у=4.

Розв'язування

Це рівняння з відокремлювальними змінними.

Домножимо обидві частини рівняння на :

Відокремимо змінні, тобто зберемо в лівій частині функцію, що залежить від у разом з , а в правій - функцію від разом з .

Для цього рівність поділимо на вираз :

.

Знайдемо інтеграл від лівої і правої частини рівняння

або

ln│y-3│=2x+ ln│C│.

Для потенціювання потрібно і праву частину останньої рівності написати зі знаком логарифма. Згідно означення логарифма маємо:

;

Тоді загальний розв'язок можна переписати у вигляді

ln│y-3│= ln + ln │C│;

потенціюючи, отримуємо:

,

тобто

- загальний розв'язок рівняння.

Розв'яжемо задачу Коші.

При х=0 , у=4

С=1.

Тоді,

- частинний розв'язок.

Відповідь: - загальний розв'язок рівняння;

- частинний розв'язок.

Приклад 6.

Розв'язати диференціальне рівняння Знайти загальний і частинний розв'язки, якщо при х=0 ; у =5.

Розв'язування

Це рівняння з відокремлювальними змінними.

Розпишемо похідну, як відношення диференціалів :

;

,

домножимо обидві частини рівняння на dx

.

Відокремимо змінні, тобто зберемо в лівій частині функцію, що залежить від y разом з , а в правій - функцію від разом з .

/ ,

Знайдемо інтеграл від лівої і правої частини рівняння

; .

Підставимо,

- загальний розв'язок диференціального рівняння.

Розв'яжемо задачу Коші.

При х=0 , у=5

C=5.

Тоді,

- частинний розв'язок.

Відповідь: - загальний розв'язок рівняння;

- частинний розв'язок.

Приклад 7. Розв'язати диференціальне рівняння

Розв'язування

Розділивши всі члени рівняння на добуток отримаємо:

Тепер змінні розділені; інтегруючи, будемо мати:

Тут довільна змінна С замінена на Скорочуючи всі члени рівняння на отримаємо:

звідки

Це і є загальний інтеграл чи загальний розв'язок даного диференціального рівняння.

Відповідь: загальний розв'язок даного диференціального рівняння.

Приклад 8. Знайти частинний розв'язок рівняння

при

Розв'язування

Відокремимо змінні, поділивши ліву і праву частини рівняння на

Інтегруємо:

або

(тут С замінено lnC )

потенціюючи, отримаємо

-- це загальний інтеграл даного диференціального рівняння.

Розв'яжемо задачу Коші.

Згідно умови, будемо мати

звідки

При цій умові із загального інтеграла отримуємо:

чи

Це і є частинний інтеграл даного диференціального рівняння. В ньому немає випадкової змінної С.

-- рівняння параболи, вершина якої лежить в точці (-1;0), вісь симетрії параболи симетрична осі

Відповідь: загальний розв'язок даного диференціального рівняння.

Вправи I

Знайти частинні розв'язки рівнянь:

1. ds = (4t-3)dt, якщо при t=0 s=0.

2 dx = (2t²-5)dt, якщо при t=1 x=-4.

3. x dx = dy, якщо при x=1 у=0.

4. x dx= y dy, якщо при x=2 y=1.

5. x²d x+ y dy = 0, якщо при х=0 у=1.

6. (t-1)dt +s ds = 0, якщо при t=2 s=0.

7. якщо при x=1 y= .

8. якщо при х=0 у=2.

9. 2s dt = t ds, якщо при t=1 s=2.

10. х²dy - y²dx = 0, якщо при х=0,2 у=1.

11. х³dy = y³dx, якщо при х= у= .

12. якщо при х=0 у=0.

13. dy + x dx =2 dx, якщо при х=1 у=1,5.

14 . якщо при х=-1 у=1.

15. (t+1)dx = 2x dt, якщо при t=1 x=4.

16. якщо при х=0 у=0.

17. , якщо при х=0 у=1.

18. , якщо при х=0 у=3.

19. , якщо при х=0 у=1.

20. , якщо при х=0 у=1.

21. , якщо при х=5 у=0.

22. , якщо при х= у= .

23. , якщо при х=0 у=4.

24. , якщо при х=0 у=1.

25. якщо у=2 при х=1

Знайти загальний розв'язок рівнянь:

26.

27. (ху² + х)dx + (x²y - y)dy = 0

28. (у - х²у)dy + (x + xy²)dx = 0.

29. (1+x²)dy - (xy + x)dx = 0.

30. y dx + ( 1 - y)x dy = 0.

31. x²dy + (y -1)dx = 0.

32. 2(xy + y)dx = x dy.

33. (x²+1)dy = y dx.

34. x²y' - 2xy = 3y.

35. Написати рівняння кривої , яка проходить через точку А (1;2), якщо кутовий коефіцієнт дотичної в кожній її точці дотику дорівнює

36. Написати рівняння кривої , яка проходить через точку А (2;1), якщо кутовий коефіцієнт дотичної в кожній її точці дотику дорівнює

37. Знайти рівняння кривої, що проходить через точку А(3;1) і має дотичну, кутовий коефіцієнт якої дорівнює 2х-1.

38 . Написати рівняння кривої, яка проходить через точку А( 4;3), якщо кутовий коефіцієнт дотичної в будь-якій точці дотику.

39. Написати рівняння кривої , яка проходить через точку А (1;3), якщо кутовий коефіцієнт дотичної в кожній її точці дотику дорівнює

Однорідні диференціальні рівняння першого порядку

Означення: Рівняння виду P dx + Q dy = 0, (1)

де Р і Q- однорідні функції, х і у однакового степеня, називаються однорідним диференціальним рівнянням першого порядку.

Для інтегрування таких рівнянь проводять заміну змінних, покладаючи , тобто

.

Ця підстановка зводить до диференціального рівняння відносно і , в якому змінні відокремлюються, після чого можна інтегрувати.

Для отримання кінцевої відповіді потрібно змінну замінити на

Наприклад, рівняння однорідне, так як множники при і одного степеня, в даному випадку другого, рахуючи по обох змінних та відразу.

Перевіримо це. Перепишемо рівняння так:

Розділимо обидві частини рівняння на добуток

тоді

Розділивши тепер чисельник і знаменник дробу (в лівій частині рівності) на отримаємо:

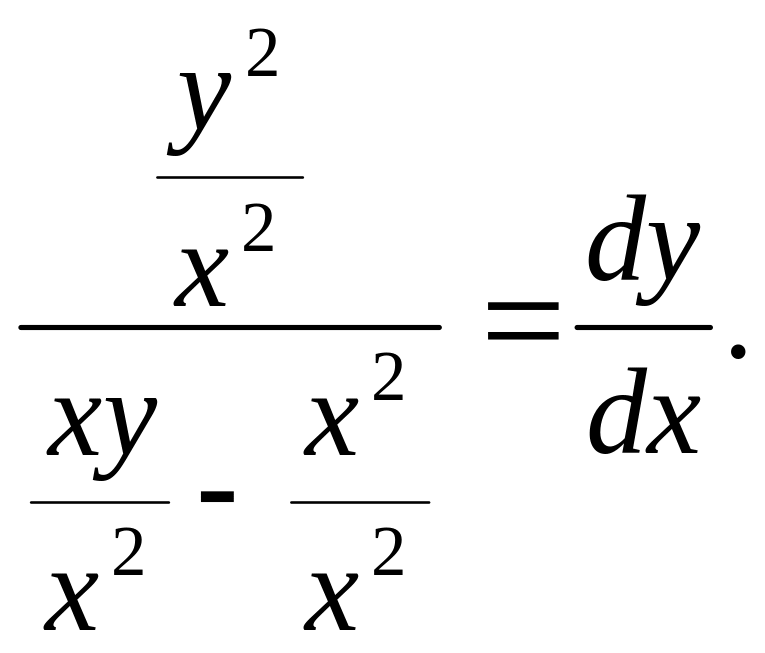
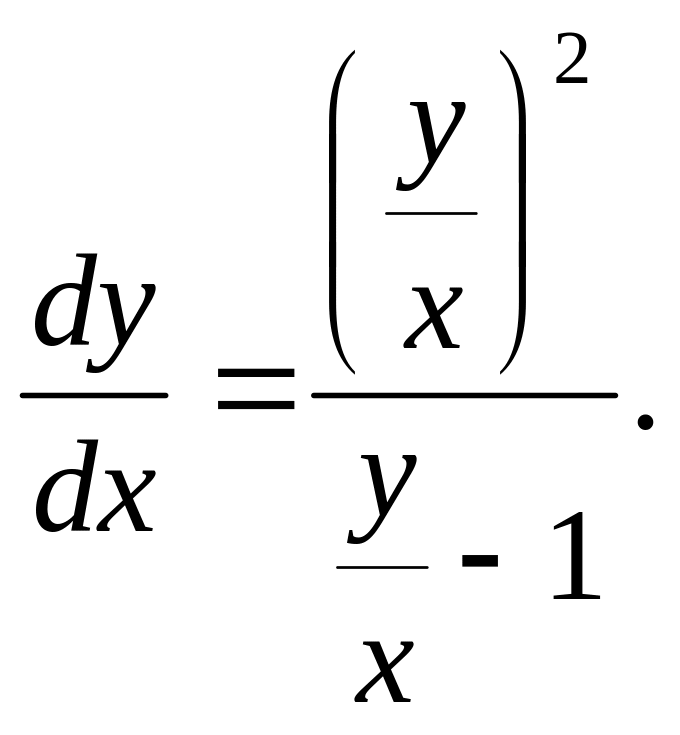
Отже, похідна

звідси, наше рівняння однорідне.

Покажемо на прикладі, як розв’язувати такі рівняння.

Приклад 9. Розв'яжіть рівняння (2)

Розв'язування

Зведемо рівняння (2) до виду (1), помноживши обидві його частини на dx:

отримаємо:

;

або

у²dx + (x²-xy)dy = 0. (3)

У рівнянні (3)

Р = у² і Q = x² - xy

Як бачимо , Р і Q - однорідні функції х та у, причому обидві функції другого степеня ; тому рівняння (2) однорідне.

Із рівняння (3) знайдемо :

/( -1)

(4)

Нехай

(5)

де z- нова функція х. Знайшовши z, ми отримаєм із рівності (5) шукану функцію

Для пошуку z продиференціюємо по х рівняння (5), застосувавши правило похідної :

,

де , а ,

тоді запишемо

(6)

Підставимо у рівняння (4) значення у і dy , взяті з рівняння (5) і (6)

(4)

одержимо

.

В одержаному рівнянні розділимо змінні:

домножимо обидві частини рівняння на

домножимо обидві частини рівняння на :

або

Відокремивши змінні у рівнянні, проінтегруємо його обидві частини:

.

В результаті інтегрування отримаємо:

, (7)

де С запишемо як ,

Тепер рівняння набуде вигляду

,

С,

або

(8)

Із рівності (5) знаходимо :

Замінивши у рівнянні (8) z знайденим його значенням, отримаємo

або

(9)

Рівняння - загальний розв'язок рівняння (2).

Відповідь: - загальний розв'язок диференціального рівняння.

Приклад 10. Розв'язати рівняння

Розв'язування

Так як це рівняння однорідне, то робимо підстановку

Диференціюємо

або

(похідна ).

Зведемо дане рівняння до вигляду (дивись перетворення у попередньому завданні)

замінимо в ньому і їхніми значеннями:

, у правій частині рівняння зведемо до спільного знаменника

або

Відділяємо змінні, помноживши обидві частини рівності на , отримаємо

у правій частині рівності почленно поділимо чисельник на знаменник

Інтегруємо:

(замість С підставлено );

Замінимо на тоді

_де

Замінюючи на С, отримаємо

Відповідь: - загальний розв'язок диференціального рівняння.

Приклад 11. Розв'язати рівняння

Розв'язування

Перепишемо рівняння так:

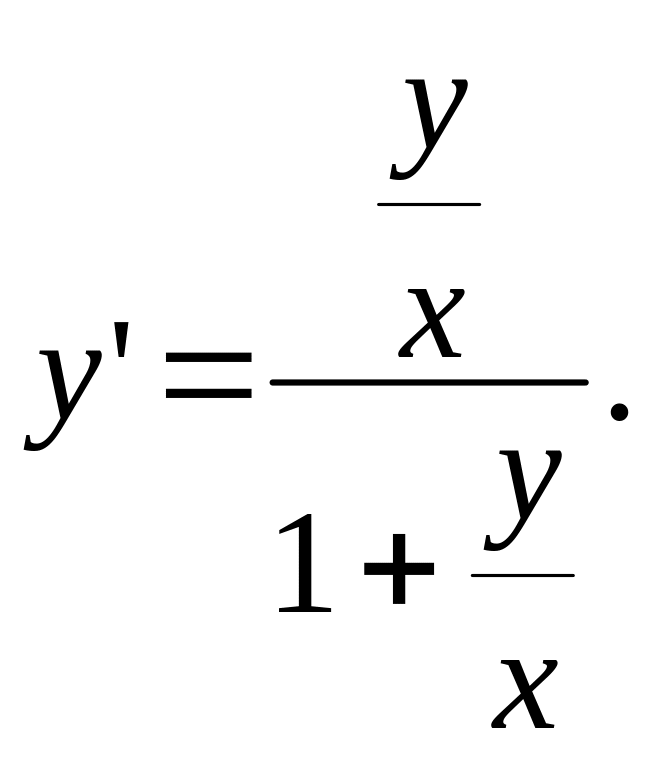
Ясно, що означає, рівняння однорідне.

Отже, звідки

Диференціюємо:

або

де ,

Замінюючи в рівнянні і їх значеннями, будемо мати:

Розділяючи змінні, маємо

Інтегруємо:

Замінюючи на отримаємо:

Це і є загальний інтеграл даного диференціального рівняння.

Відповідь: - загальний розв'язок диференціального рівняння.

Вправи II

Знайти загальний розв'язок рівнянь:

1. (х + у)dx + x dy = 0.

2. (x-y)y dx = x² dy .

3. .

4. xy² dy = (x³+y³) dx .

5. (x² - 2y²)dx + 2xy dy = 0.

6. (x + y)dx + (y - x)dy = 0.

7. x dy - y dx = y dy .

8. 

9. .

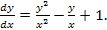
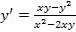Знайти частинні розв'язки рівнянь:

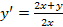10. , якщо у = 0 при х = 1.

2х

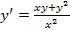11. , якщо у = 1 при х = 1.

12. якщо у = 2 при х = 2.

Лінійні диференціальні рівняння

Означення: Лінійними диференціальними рівняннями називаються такі рівняння, які містять невідому функцію і її похідну тільки в першій степені.

Такі рівняння мають вигляд:

або

Якщо то рівняння називається лінійним рівнянням без правої частини.

Для розв’язування лінійних рівнянь користуються підстановкою де і -- деякі функції від : тобто, розкладається на два множника.

Маємо на увазі, що ця операція не повністю визначена. Наприклад, якщо то цю функцію можна розкласти на множники багатьма способами:

і т.д.

Через це, покладаючи один із множників можна вибрати довільно.

Розглянемо розв’язування лінійних рівнянь на прикладах.

Приклад 12. Розв’язати рівняння

Розв'язування

Тут -- рівняння лінійне; отже

тоді

замінюючи і їх значеннями, отримаємо:

Виносячи в другому і третьому доданках з а дужки, рівняння перепишемо так:

Виберемо так, щоб вираз в дужках перетворився на нуль. Це справедливо, так як співмножник в рівності беремо довільно.

Нехай

розділяємо змінні, маємо:

довільну змінну С можна не писати (в даному випадку беремо змінну, рівну 0).

Тепер рівняння набуде вигляду

,

,

.

(Тут С писати обов’язково, інакше вийде не загальний розв'язок , а частинний ). Тепер знайдемо шукану функцію, пам’ятаючи, що

або