Міністерство освіти і науки України

Бердичівський коледж промисловості, економіки та права

Волошина З. П.

Методична розробка

з дисципліни «Основи вищої математики»

на тему: «Криві другого порядку »

для студентів другого курсу спеціальності 5.05050302

« Технологія обробки матеріалів на верстатах і автоматичних лініях»

Бердичів 2009

Автор-укладач З.П. Волошина

Методична розробка з дисципліни «Основи вищої математики» на тему: « Криві другого порядку»

У даній методичній розробці викладено, у розширеному вигляді, матеріал щодо вивчення кола, еліпса, гіперболи, параболи. Для кожної з кривих другого порядку наведено хід виведення канонічного рівняння, сформульовані їх властивості та поняття ексцентриситету.

Для еліпса і гіперболи розглянуто окремі випадки розташування їх фокусів на осі ОХ та ОY, відповідні канонічні рівняння, дано означення та поняття рівносторонньої гіперболи, її асимптот.

У методичній розробці наведено 4 види канонічних рівнянь параболи, симетричної відносно осі ОХ (ОY), із вершиною початку координат і вітки якої напрямлені вправо, вліво (вгору, вниз),рівняння директрис. Розглянуто 4 типи рівнянь параболи із суміщеною вершиною,та їх характеристика.

Блок навчально-методичного забезпечення кожної теми включає в повному обсязі викладений теоретичний матеріал, детально наведені приклади на закріплення цього матеріалу.

В кінці розробки вказано використану літературу.

Розробка розрахована для студентів другого курсу спеціальності «Технологія обробки матеріалів на верстатах і автоматичних лініях».

Розглянуто на засіданні циклової комісії

фізико-хіміко-математичних дисциплін

Протокол № від 2009р.

Голова циклової комісії:

О.О.Горленко.

План

• Криві другого порядку на площині.

• Коло.

• Еліпс.

• Гіпербола.

• Парабола.

• Канонічні рівняння кривих другого порядку.

К р и в і д р у г о г о п о р я д к у н а п л о щ и н і

            Множині рівнянь, що зв’язують дві змінні у деякій плоскій системі координат, відповідає множина кривих найрізноманітніших форм. Пряма лінія – частинний випадок кривої. Криву можна розглядати як слід переміщення точки. У математиці криву задають аналітично, тобто її рівнянням.  Тут ми розглянемо лише криві другого порядку, тобто їх рівняння є алгебраїчними рівняннями відносно двох змінних, які входять у нього не вище як у другому степені. Отже, в загальному плані крива другого порядку описується рівнянням

           

де A,B,C,D,E - деякі коефіцієнти, які можуть приймати різні значення.

Коефіцієнти A, B, C одночасно нулю дорівнювати не можуть.

           Найпоширеніші з кривих другого порядку – еліпс і його частинний випадок – коло, гіпербола і парабола.

Про еліпс згадується ще у середній школі у зв’язку з вивченням закону всесвітнього тяжіння і рухом планет навколо Сонця та рухом штучних супутників навколо Землі. Спостерігаючи за рухом планет навколо Сонця, Кеплер склав таблиці, що описували їх положення на небесній сфері і підтверджували той факт, що всі планети рухаються навколо Сонця по еліпсах. Французький вчений Левер’є, аналізуючи таблиці Кеплера, прийшов до висновку, що в русі останньої на той час планети Уран спостерігаються значні відхилення від еліптичної траєкторії. Він робить припущення, що причиною цих відхилень є невідома на той час планета, яка знаходиться далі від Сонця, ніж Уран. Після тривалих і складних обчислень він знаходить координати нової планети. Тому про нову планету (її потім було названо Нептуном) кажуть, що вона була відкрита “на кінчику олівця”.

            З еліпсом доводиться мати справу і в техніці: еліптичний циркуль для креслення еліпса і на його зворотній дії побудовано патрон Леонардо да Вінчі для верстатів, за допомогою яких обробляються деталі з перерізом еліптичної форми. У конструкціях ряду верстатів застосовуються зубчасті еліптичні передачі (рис.1). Загальновідомо також, що від прожектора світлові промені йдуть паралельним пучком, а їх дзеркала параболічні, тобто будь-який їх осьовий переріз є параболою. І навпаки, лінза з осьовим параболічним перерізом збирає паралельні промені в одну точку. На цій основі можна за допомогою такої лінзи одержувати в її фокусі високі температури.

  Рис.1          

Більшість типів ліній другого порядку відомі давно, їх досить добре вивчив Аполлоній. Він утворював основні типи ліній другого порядку як плоскі перерізи кругового конуса, тому в математичній літературі лінії другого порядку відомі ще як конічні перерізи.

Лінії другого порядку зустрічаються в явищах навколишнього світу: по еліпсу рухаються планети Сонячної системи, по гіперболі або параболі — комети. Траєкторія руху тіла, кинутого під кутом до горизонту, є параболою.

К о л о

Y

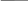M(x;y)

оооооо

X

0

Означення: Множина точок, що знаходяться на однаковій відстані від заданої точки центра, називається колом.

З означення ОМ=R або . (1)

Піднесемо обидві частини до квадрату, одержимо

= - канонічне рівняння кола.

Тут ( ; ) - координати центра кола, - радіус кола.

Якщо центр кола знаходиться в точці О(0;0), то його рівняння має вигляд

= . (2)

Якщо у рівнянні (1) розкрити дужки, то можна записати

. (3)

Помноживши обидві частини рівності (3) на число А ≠ 0 та позначивши

-2Aa=B, -2bA=C, A( )=D,

дістанемо рівняння кола вигляду

, (4)

яке називають загальним рівнянням кола.

Рівняння кола має такі властивості:

1)воно другого степеня відносно і ;

2)коефіцієнти при квадратах і рівні;

3)відсутній член з добутком .

Приклади розв’язування задач

Приклад1. Знайти центр та радіус кола, яке задано рівнянням

.

Розв΄язання:

Якщо рівняння кола задано у загальному вигляді, то визначимо координати центра цього кола та його радіус . Зведемо рівняння до канонічного вигляду. З цією метою згрупуємо члени і так, щоб утворились повні квадрати і при цьому не порушилась еквівалентність рівнянь:

,

,

,

.

Отже, С ( , = 2.

Відповідь: С ( , = 2.

Приклад 2. Написати рівняння лінії центрів двох кіл і

Розв΄язання:

Знайдемо спочатку координати центрів цих двох кіл, виділивши повні квадрати

,

,

,

,

,

.

Отже, координати центру першого кола С₁(3;-4), а другого С₂(-1;6). Використовуючи рівняння прямої через дві точки, запишемо

,

10( = - 4( ),

10 = - 4 ,

10 + = 0,

5 = 0 – шукане рівняння центрів кіл.

Відповідь: 5 = 0.

Приклад 3. Скласти рівняння кола радіусом =5 з центром в точці А( 3; - 2).

Розв΄язання:

Підставивши значення =5, a = 3, b = - 2 в канонічне рівняння кола, знайдемо

.

Відповідь: .

Е л і п с

Означення:   Еліпсом називається геометричне місце точок площини, сума відстаней від яких до двох заданих точок (фокусів) є величиною сталою  і більшою за відстань між фокусами.

Виведемо рівняння еліпса. Через F₁ , F₂ позначимо фокуси, 2с - відстань між ними (F₁ F₂ = 2с або фокальна відстань) , 2а – суму відстаней від довільної точки еліпса до фокусів. За означенням еліпса 2а >2с, тобто а >с. Через точки F₁ ,F₂ проведемо вісь абсцис, а вісь ординат спрямовуємо так, щоб вона проходила через середину відрізка F₁ F₂ перпендикулярно до осі ОХ

У вибраній системі координат точки F₁ ,F₂ мають координати : F₁(-с;0), F₂(с;0). Виберемо на еліпсі довільну точку М( х; y ). За означенням еліпса

F₁ М + F₂ М = 2а. (1)

Запишемо рівність (1) у координатах.

За формулою відстані між двома точками А(х_1; у_1; ) , B (х_2; у_2; )

׀АВ׀ = _{дістанемо}

, (2)

Рівняння (2) є аналітичним рівнянням еліпса.

На перший погляд, не зрозуміло, чи належить рівняння (2) до рівнянь кривих другого порядку. Виконаємо деякі перетворення рівняння (2), зокрема, звільнимося від ірраціональності. Перенесемо один корінь у праву частину й піднесемо обидві частини рівності до квадрата :

,

,

, виконаємо спрощення

,

,

знову піднесемо обидві частини рівності до квадрата:

, розкриємо дужки

, спростимо

,

. (3)

Оскільки F₁ М + F₂ М = 2а, а за означенням еліпса 2а >2с, то > 0.

Позначимо .

Тоді рівність (3) запишемо так:

.

Поділивши обидві частини цієї рівності на , дістанемо

, а >b. (4)

cпіввідношення між а, b і c:

Рівняння (4) канонічне рівняння еліпса, фокуси якого лежать на осі ОХ.

В л а с т и в о с т і е л і п с а

1.Еліпс належить до кривих другого порядку ( це випливає із канонічного

рівняння еліпса).

2.Еліпс є обмеженою кривою.

3.Еліпс має вертикальну та горизонтальну осі симетрії, а також центр симетрії.

4.Еліпс перетинає осі координат у точках A₁(-a;0), A₂ (a;0),B₁(0;-b), B₂(0; b), які є вершинами еліпса.

Величини 2а і 2b називаються відповідно великою та малою осями еліпса, а а і b - напівосями.

( Таким чином, еліпс вміщується в прямокутник із сторонами 2а і 2b.Сторони прямокутника дотикаються до еліпса в його вершинах. )

5. За напівосями можна побудувати еліпс

(беруть нерозтяжну нитку довжиною 2а; кінці нитки закріплюють у фокусах F₁ і F₂ ; олівцем натягують нитку і креслять еліпс).

Якщо у канонічному рівнянні еліпса а = b, то дістанемо рівняння кола =

з центром у початку координат і радіусом b.

( Оскільки для еліпса , то при а = b маємо с =0. Таким чином, коло – це еліпс, у якого фокуси збігаються з центром симетрії, тобто фокальна відстань дорівнює нулю.)

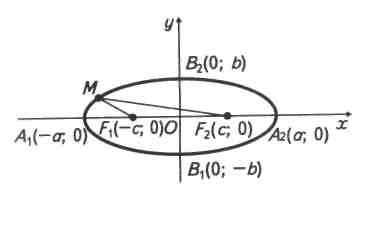
Еліпс, фокуси якого лежать на осі ОY

Якщо фокуси еліпса F₁(0;c ), F₂(0 ;- c) лежать на осі ОY, то його канонічне рівняння має вигляд

, b > а (5)

cпіввідношення між а, b і c:

Координати вершин еліпса A₁(a;0), A₂ (-a;0),B₁(0;b), B₂(0; -b),

B₁ B₂ = 2b – велика вісь,

A₁ A₂ = 2a – мала вісь,

F₁ F₂ = 2с - фокальна відстань.

Слід зауважити, що звичайним циркулем еліпс побудувати неможливо, бо будь-якої довжини дуга не може збігатися з будь-якою частиною еліпса. Фігура, подібна за формою до еліпса і побудована за допомогою циркуля, не еліпс, а овал. Еліпс одержується механічно шляхом обертання гнучкого круга кільцевої форми.

Ексцентриситет еліпса 

Для характеристики еліпса вводять поняття ексцентриситета еліпса, який характеризує відхилення еліпса від кола – степінь «витягнутості» еліпса.

Означення:  Ексцентриситетом еліпса називається відношення відстані між фокусами до довжини великої осі.

Ексцентриситет еліпса  позначається буквою ε:

ε або ε .

Оскільки, за означенням 2а >2с, то ексцентриситет еліпса  ε завжди є правильним дробом, тобто 0 ε .

Якщо величина ексцентриситету еліпса  ε ≈ 1, то еліпс сильно «витягнутий» уздовж

великої осі; при малому значенні ексцентриситету еліпса  ε (ε ≈ 0) еліпс близький до кола. Якщо ε = 0, то еліпс перетворюється в коло.

Приклади розв’язування задач

Приклад 1. Еліпс задано рівнянням . Визначити довжину його осей, координати вершин і фокусів.

Розв΄язання:

Зведемо рівняння еліпса до канонічного рівняння, поділивши обидві частини даного рівняння на 36, дістанемо

.

звідки і , або а = 3 і b = 2. Отже, велика вісь еліпса A₁ A₂ = 2а=6, мала B₁ B₂ = 4.

Вершинами еліпса будуть точки A₁(-3;0), A₂ (3;0),B₁(0;-2), B₂(0; 2). Для відшукання фокусів використаємо , звідки

,

.

Отже, фокусами будуть точки F₁(- ;0), F₂( ;0).

Відповідь: довжини осей - A₁ A₂ =6, B₁ B₂ = 4;координати вершин - A₁(-3;0), A₂ (3;0),B₁(0;-2), B₂(0; 2); координати фокусів - F₁(- ;0), F₂( ;0).

Приклад 2. Знайти координати фокусів, довжини осей і ексцентриситет еліпса, заданого рівнянням   .

Розв΄язання:

Зведемо рівняння еліпса до канонічного рівняння, поділивши обидві частини рівності на 32 :

,

.

Одержали, що , , звідки а = 4 і b = .

Оскільки b> а, то фокуси еліпса розташовані на осі ординат. Вони мають координати F₁(0;c ), F₂(0 ;- c), де знаходимо із співвідношення .

Підставимо значення а = 4 і b , одержимо

; , c = 4.

Отже, фокусами будуть точки F₁(0; 4), F₂(0 ;-4).

Знайдемо: велику вісь еліпса 2b = ; малу вісь 2a = 8; ексцентриситет еліпса 

ε .

Відповідь: координати фокусів - F₁(0; 4), F₂(0 ;-4); довжини осей - 2b = , 2a = 8;

ε .

Приклад 3. Скласти канонічне рівняння еліпса, у якого мала вісь дорівнює 6, а відстань між фокусами - 8.

Розв΄язання:

Оскільки мала вісь 2b = , а 2с = 8, то b = , c = 4. Тоді фокуси розташовані на осі ОХ.

Із cпіввідношення між а, b і c: , знайдемо а:

,

, тобто .

Отже, канонічне рівняння еліпса має вигляд .

Відповідь: .

Приклад 4. Записати канонічне рівняння еліпса, що проходить через точку М(5;0), якщо фокальна відстань дорівнює 6.

Розв΄язання:

Оскільки відстань між фокусами дорівнює 6, то с= 3. За умовою точка М(5;0) належить еліпсу, тож її координати задовольняють рівняння еліпса . Тому , .

Із рівності знаходимо .

Отже, шукане рівняння

.

Відповідь:

Приклад 5. Звести до канонічного вигляду рівняння і показати, що воно є рівнянням еліпса. Знайти координати фокусів.

Розв΄язання:

Перепишемо дане рівняння у вигляді і поділимо обидві його частини на 3600:

.

Це рівняння еліпса. Оскільки для еліпса і , , то

, тобто с = 8. Фокуси еліпса знаходитимуться в точках F₁(-8; 0), F₂(8 ;0).

Відповідь: Фокуси еліпса F₁(-8; 0), F₂(8 ;0).

Приклад 6. Записати рівняння еліпса, фокусами якого є точки (0;- ) і ( ), а велика вісь дорівнює 6.

Розв΄язання:

Фокуси еліпса лежать на осі ОY, отже, 2b= 6, тоді b= 3.

За формулою знаходимо . Підставивши значення і в канонічне рівняння, маємо .

Відповідь: .

Приклад 7. Записати рівняння еліпса з фокусами на осі ОХ, якщо відстань між фокусами дорівнює 12, а ексцентриситет ε = 0,6.

Розв΄язання:

За умовою задачі F₁ F₂ = 2с=12, отже, с=6, ε = = 0,6. Підставивши в цю рівність значення с = 6, дістанемо , тобто a = 10.

За формулою знайдемо .

Отже, шукане рівняння має вигляд

.

Відповідь: .

Г і п е р б о л а

Означення:  Гіперболою називають геометричне місце точок площини, для яких модуль різниці відстаней до двох заданих точок (фокусів) є величиною сталою  й меншою, ніж відстань між фокусами.

Виведемо рівняння гіперболи. Виберемо систему координат таким чином, щоб вісь ОХ проходила через фокуси F₁ і F₂ , а вісь ОY – через середину відрізка F₁ F₂ перпендикулярно до нього. Тоді у вибраній системі координат фокуси мають координати: F₁(-с;0), F₂(с;0).

Візьмемо на гіперболі довільну точку М( х; y ).

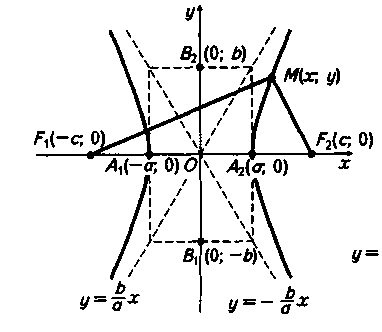
За означенням гіперболи відстань між фокусами 2с більша за різницю відстаней до фокусів 2а, тому 2с >2а або а < с і маємо ,

. (1)

Запишемо рівність (1) у координатах.

За формулою відстані між двома точками А(х_1; у_1; ) , B (х_2; у_2; )

׀АВ׀ = _{дістанемо}

, (2)

Перенесемо один корінь у праву частину й піднесемо до квадрата обидві частини рівності:

,

,

,

виконаємо спрощення :

,

,

,

поділимо ліву і праву частини рівності на 4:

,

знову піднесемо обидві частини рівності до квадрата:

,

),

розкриємо дужки

,

,

згрупуємо доданки

,

,

(3)

Оскільки за означенням гіперболи F₁ F₂ >( , тобто 2с >2а , то >0.

Позначимо .

Тоді рівність (3) запишемо так:

.

Поділивши обидві частини цієї рівності на , дістанемо

(4)

Рівняння (4) канонічне рівняння гіперболи , фокуси якої лежать на осі ОХ.

cпіввідношення між а, b і c:

В л а с т и в о с т і г і п е р б о л и

1.Гіпербола є кривою другого порядку .

2. Гіпербола є необмеженою кривою.

3.Гіпербола має вертикальну та горизонтальну осі симетрії (осі координат), а центром симетрії є початок координат.

4. Гіпербола перетинає вісь абсцис у двох точках A₁(-a;0), A₂ (a;0), які є вершинами гіперболи (дійсними вершинами), а вісь ординат не перетинає.

5.Гіпербола визначається параметрами а і b, а і с.

Величини 2а і 2b називаються відповідно дійсною віссю та – уявною віссю гіперболи , а величини а і b - її півосями.

6.Прямі є асимптотами гіперболи ( асимптота гіперболи - це пряма, яка має властивість: точка на гіперболі , яка віддаляється від початку координат у нескінченність,необмежено наближається до цієї прямої).

Гіпербола, фокуси якої лежать на осі ОY

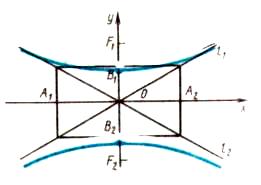
Якщо фокуси еліпса F₁(0;c ), F₂(0 ;- c) лежать на осі ОY, то її канонічне рівняння має вигляд

(5)

cпіввідношення між а, b і c:

B₁ B₂ = 2b – дійсна вісь,

A₁ A₂ = 2a – уявна вісь,

F₁ F₂ = 2с - фокусна відстань.

B₁(0;b), B₂(0;-b) – вершини гіперболи.

Побудова гіперболи

Будуємо основний прямокутник зі сторонами 2а і 2b ; проводимо прямі,що збігаються з діагоналями цього прямокутника , тобто проводимо асимптоти ; потім креслимо гіперболу.

Ексцентриситет гіперболи 

Означення:  Ексцентриситетом гіперболи  називається відношення відстані між фокусами до довжини дійсної осі.

Ексцентриситет  гіперболи позначається буквою ε:

ε або ε .

Оскільки, за означенням 2а < 2с, то ексцентриситет гіперболи ε завжди є неправильним дробом, тобто ε .

Асимптоти гіперболи

Рівняння асимптот гіперболи :

.

Рівностороння гіпербола

Означення: Гіпербола називається рівносторонньою, якщо довжина її дійсної осі дорівнює довжині уявної осі, тобто 2а = 2b

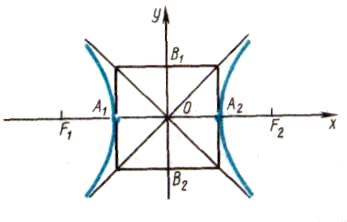
Канонічне рівняння рівносторонньої гіперболи , фокуси якої лежать на осі ОХ.

або

Канонічне рівняння рівносторонньої гіперболи , фокуси якої лежать на осі ОY .

або

Для рівносторонньої гіперболи справедливе співвідношення:

, тобто .

Ексцентриситет рівносторонньої гіперболи 

ε , тобто ε

Асимптоти рівносторонньої гіперболи

Рівняння асимптот для рівносторонньої гіперболи має вигляд

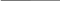
, тобто

асимптоти рівносторонньої гіперболи є бісектрисами координатних кутів.

П р и к л а д и р о з в ’я з у в а н н я з а д а ч

Приклад 1. З'ясувати, яку лінію визначає рівняння .

Розв΄язання:

Поділивши обидві частини рівняння на 63, дістанемо

Порівнюючи дане рівняння з канонічним рівнянням гіперболи, зробимо висновок, що рівняння визначає гіперболу з дійсною піввіссю а = 3 та уявною піввіссю b= .

Приклад 2. Дано асимптоти гіперболи у = ± х і відстань між фокусами 2с = 10.

Записати рівняння гіперболи.

Розв΄язання:

Із рівнянь асимптот гіперболи випливає, що , звідки а = 2b .

Користуючися рівністю , дістаємо , звідки .

Тоді .

Запишемо шукане рівняння гіперболи:

.

Відповідь:

Приклад 3. Дано гіперболу Визначити довжину її осей і відстань між

фокусами .

Розв΄язання:

З канонічного рівняння гіперболи маємо: , або а = 4; , або b= 3.

За cпіввідношенням між а, b і c: знаходимо с:

, звідки с= 5, а тому відстань між фокусами 2с= 10.

Відповідь: а = 4 , b= 3, 2с= 10.

Приклад 4. Знайти координати фокусів, довжини осей і ексцентриситет і рівняння асимптот гіперболи , заданої рівнянням   .

Розв΄язання:

Зведемо рівняння гіперболи до канонічного рівняння, поділивши обидві частини рівності на 400:

,

.

З цього рівняння ми бачимо, що фокуси гіперболи розташовані на осі абсцис (ОХ), запишемо , , тобто а = 5 , b= 4.

За cпіввідношенням між а, b і c: знаходимо с:

, звідки с= .

Отже, фокусами гіперболи будуть точки F₁(- ;0), F₂( ;0);

дійсна вісь гіперболи 2а = 10; уявна вісь 2b= 8.

Знайдемо ексцентриситет гіперболи : ε  

ε .

Рівняння асимптот гіперболи : ,

.

Відповідь: фокуси гіперболи - F₁(- ;0), F₂( ;0);

дійсна вісь 2а = 10; уявна вісь 2b= 8; ексцентриситет гіперболи - ε ; рівняння асимптот - .

! Приклад 5. Скласти канонічне рівняння гіперболи з фокусами на осі ОХ, якщо відстань між ними дорівнює , а рівняння асимптот .

Розв΄язання:

Оскільки, F₁ F₂ = 2с = , то с=

За cпіввідношенням між а, b і c: знаходимо :

.

За умовою, . Підставивши значення с= в складемо систему рівнянь:

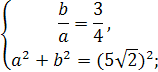
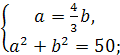
Підставимо значення у рівняння , одержимо:

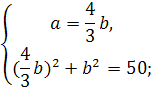
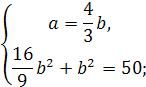
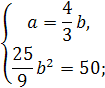
Звідси одержимо

Підставимо значення у канонічне рівняння гіперболи:

.

Відповідь: канонічне рівняння гіперболи - .

Приклад 6. Знайти вершини, фокуси, ексцентриситет і асимптоти гіперболи

Розв΄язання:

Зведемо рівняння даної гіперболи до канонічного вигляду ( помноживши ліву і праву частини рівності на (-1)):

, .

Це є канонічне рівняння гіперболи, фокуси якої лежать на осі ОY. Із рівняння маємо,що

, , тобто b = 8, a= 6. Тоді вершини гіперболи знаходяться в точках B₁(0;8) і B₂(0;-8).

За cпіввідношенням між а, b і c:

знайдемо с: , звідси с = 10.

Отже, фокусами гіперболи є точки: F₁(0;10 ), F₂(0 ;- 10).

Ексцентриситет гіперболи обчислимо за формулою ε ,

ε .

асимптоти гіперболи знаходимо за формулою ,

x.

Відповідь: вершини гіперболи - B₁(0;8) і B₂(0;-8);

фокуси - F₁(0;10 ), F₂(0 ;- 10);

ексцентриситет ε ;

асимптоти .

П а р а б о л а

Означення: Параболою називають геометричне місце точок площини, відстані від яких до заданої точки (фокуса) й заданої пря­мої (директриси) рівні.

Виведемо рівняння параболи.

Нехай на площині дано точку F та пряму d . Візьмемо таку систему координат хОу, щоб вісь абсцис (ОХ) про­ходила через фокус F перпендикулярно до прямої d, а вісь ординат ( OY) ділила відстань між фокусом і директрисою навпіл (рис.1 ).

Відстань між фо­кусом і директрисою параболи позначимо через р: AF=p

За означенням р > 0, тоді точка F має координати ( ,

а рівнянням дире­ктриси є

Нехай М (х, у) — довільна точка площини. Точка М, за означенням, буде точкою параболи тоді і тільки тоді, коли . (1)

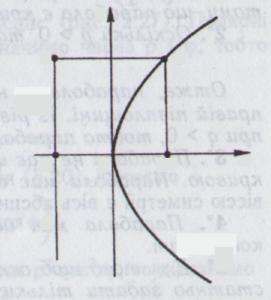Y

B ( B M (x;y) Відрізок FM - фокальний

радіус т. М параболи

                             

A O F( X

d

мал.1

Запишемо рівність (1) у координатах.

За формулою відстані між двома точками А(х_1; у_1; ) , B (х_2; у_2; )

׀АВ׀ = _{дістанемо}

,

.

Оскільки , за означенням параболи, , то отримаємо

(2)

Піднесемо обидві частини рівності (2) до квадрату й здійснимо перетворення:

,

,

,

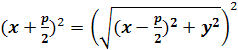, p>0 (3)

1. Канонічне рівняння параболи, симетричної відносно осі ОХ, із вершиною в

початку координат і вітки якої напрямлені вправо ( мал.1)

, p>0

координати фокуса F ( ,

рівняння дире­ктриси .

Y

B M (x;y)

                             

A O F( X

d

мал.1

2. Канонічне рівняння параболи, симетричної відносно осі ОХ, із вершиною в початку координат і вітки якої напрямлені вліво (мал.2)

, p>0

координати фокуса F (- ,

рівнянням дире­ктриси .

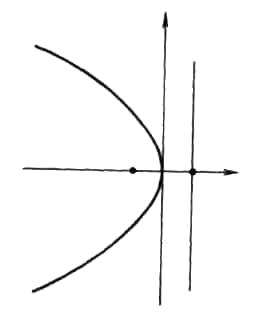Y

                                     

            F(- O X

мал.2

3. Канонічне рівняння параболи, симетричної відносно осі OY , із вершиною в початку координат і вітки якої напрямлені вгору (мал. 3)

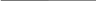
, p > 0

Y

F(0; )

y = - O X

мал.3

координати фокуса F ( ,

рівняння дире­ктриси . (див. мал.3)

4. Канонічне рівняння параболи, симетричної відносно осі OY , із вершиною в початку координат і вітки якої напрямлені вниз (мал.4)

, p > 0

координати фокуса F ( ,

рівняння дире­ктриси . (див.мал.4)

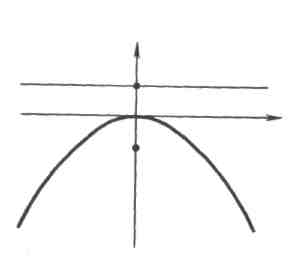Y

y =

O X

F

мал. 4

В л а с т и в о с т і п а р а б о л и

1. Парабола є кривою другого порядку .

2.Парабола є необмеженою кривою.

3.Парабола має одну вісь симетрії.

4. Парабола має одну вершину, яка лежить в початку координат.

5.Для того щоб скласти канонічне рівняння параболи, достатньо задати тільки величину p, яка називається параметром параболи.

Рівняння параболи із суміщеною вершиною

Розглянемо тепер параболу, симетричну відносно прямої, паралельної осі ОХ (осі OY),

вершина якої міститься не у початку координат, а у довільній точці А(a;b) (у прямокутній системі координат хОу).

1. Рівняння параболи з вершиною в точці а(a;b), з віссю симетрії, паралельною осі ох, і вітками, напрямленими вправо ( мал.5 a))

, де

параметр параболи - відстань від фокуса параболи до її директриси.

Якщо у параболи вітки напрямлені вправо, то її директриса розміщена від вершини

параболи - вліво (на одиниць).

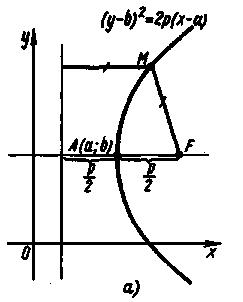
мал.5

2. Рівняння параболи з вершиною в точці а(a;b), з віссю симетрії, паралельною осі ох, і вітками, напрямленими вліво ( мал.5 б))

, де

параметр параболи - відстань від фокуса параболи до її директриси.

Якщо у параболи вітки напрямлені вліво , то її директриса розміщена від вершини

параболи - вправо (на одиниць) .

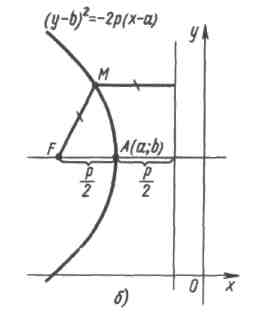
мал.5

3. Рівняння параболи з вершиною в точці а(a;b), з віссю симетрії, паралельною осі oy , і вітками, напрямленими вгору ( мал.6 а))

, де

параметр параболи - відстань від фокуса параболи до її директриси.

Якщо у параболи вітки напрямлені вгору , то її директриса розміщена від вершини

параболи - вниз (на одиниць) .

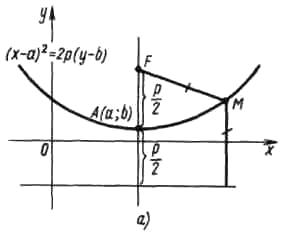
мал. 6

4. Рівняння параболи з вершиною в точці а(a;b), з віссю симетрії, паралельною осі oy , і вітками, напрямленими вниз ( мал.6 б))

, де

параметр параболи - відстань від фокуса параболи до її директриси.

Якщо у параболи вітки напрямлені вниз, то її директриса розміщена від вершини

параболи - вгору (на одиниць) .

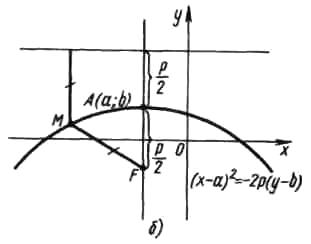
мал. 6

П р и к л а д и р о з в ’я з у в а н н я з а д а ч

Приклад 1. Скласти рівняння параболи з вершиною в початку координат, якщо її фокус

знаходиться в точці F ( .

Розв΄язання:

Оскільки, фокус параболи знаходиться в точці F ( , то скористаємося канонічним рівнянням параболи, симетричної відносно осі ОХ, із вершиною в початку координат і вітки якої напрямлені вправо

, p>0.

За координатами фокуса F ( знайдемо p:

, звідки p= 6.

Підставивши значення p= 6 в канонічне рівняння , одержимо:

.

Відповідь: .

Приклад 2. Знайти координати фокуса, рівняння параболи з вершиною в початку

координат, якщо її рівняння директриси .

Розв΄язання:

Канонічним рівнянням параболи з вершиною в початку координат є рівняння виду,

, p>0, так як задано рівняння директриси .

Загальне рівняння директриси має вигляд . Підставивши значення в рівняння , одержимо:

, p= 8.

Канонічне рівняння параболи з вершиною в початку координат буде мати вигляд

.

Знайдемо координати фокуса F ( . Тоді маємо F ( , F (

Відповідь: , F ( .

Приклад 3. Знайти координати фокуса і рівняння директриси параболи, яка задана

рівнянням .

Розв΄язання:

Із даного канонічного рівняння маємо, що ,тобто p= 4, звідки .

Знайдемо координати фокуса F ( і рівняння дире­ктриси :

F ( , .

Відповідь: координати фокуса F ( , рівняння дире­ктриси .

Приклад 4. Скласти канонічне рівняння параболи з вершиною в початку координат і рівняння її директриси, якщо фокус знаходиться в точці F ( .

Розв΄язання:

Якщо фокус параболи знаходиться в точці F ( , то її канонічне рівняння має вигляд , p > 0.

Координати фокуса F ( відомо, тому , тобто p= 6.

Отже, канонічним рівнянням параболи буде рівняння: . Запишемо рівняння дире­ктриси , тобто, .

Відповідь: канонічне рівняння параболи ,

рівняння дире­ктриси .

Приклад 5. Дано рівняння параболи . Скласти рівняння її

директриси.

Розв΄язання:

Рівняння параболи нагадує рівняння параболи з вершиною в точці А(a;b), з віссю симетрії, паралельною осі ОХ, і вітками, напрямленими вправо або вліво ( , або .

Знайдемо координати вершини параболи.

Для цього перетворимо задане рівняння:

, ,

у лівій частині даного рівняння виділимо повний квадрат двочлена

,

,

,

звідки , . Тоді А(1;2).

, тобто є рівнянням параболи з вершиною в точці А(1;2), з віссю симетрії, паралельною осі ОХ, і вітками, напрямленими вправо.

Знайдемо : із рівняння видно що , .

Якщо у параболи вітки напрямлені вправо, то її директриса розміщена від вершини

параболи - вліво (на одиниць). Так як, відстань від вершини параболи до осі OY рівна 1, а від вершини до директриси рівна 5, то абсциса директриси дорівнює різниці

;

Рівняння директриси: .

Відповідь: Рівняння директриси .

Приклад 6. Дано рівняння параболи . Скласти рівняння її осі та

директриси.

Розв΄язання:

Рівняння параболи нагадує рівняння параболи з вершиною в точці А(a;b), з віссю симетрії, паралельною осі ОХ, і вітками, напрямленими вправо або вліво ( , або .

Знайдемо координати вершини параболи.

Для цього перетворимо задане рівняння:

. , ,

у лівій частині даного рівняння виділимо повний квадрат двочлена:

,

,

,

, звідки , . Тоді А(-2;3).

, тобто є рівнянням параболи з вершиною в точці А(-2;3), з віссю симетрії, паралельною осі ОХ, і вітками, напрямленими вправо.

Вісь параболи проходить через вершину А(-2;3), паралельно осі ОХ, тому її рівняння осі буде мати вигляд : .

Знайдемо : із рівняння видно що , .

Якщо у параболи вітки напрямлені вправо, то її директриса розміщена від вершини

параболи - вліво (на одиниць).

Так як, відстань від вершини параболи до осі OY рівна (-2), а від вершини до директриси рівна 2 то абсциса директриси буде дорівнювати ( -4), тобто .

Відповідь: Рівняння директриси , рівняння осі - .

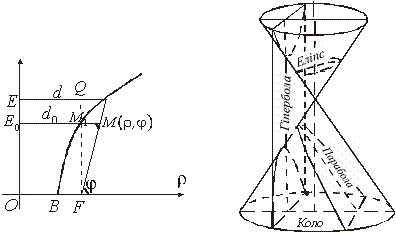
Вказані три криві мають спільне походження: всі вони є певними перерізами двопорожнинного конуса. Цей факт чудово ілюструється малюнком і вказує на джерело універсальності трьох розглянутих кривих.

Використана література:

1. Вища математика. Ч 1.За загальною редакцією П.П.Овчинникова.Київ 2003р.

2. М.В. Грисенко Математика для економістів. Навчальний посібник. Київ 2007р.

3. Н.В. Богомолов Практические занятия по математике. Москва1990г.

4. В.Т. Лисичкин Математика .Москва 1991г.

5. В.М. Лейфура Математика. Київ 2003р.

6. И.И. Математика для техникумов. Москва 1989 г.

7. Вища математика: Навчально-методичний посібник для самостійного вивчення дисципліни (К.Г. Валєєв, І.О.Джалладова, О.І. Лютий та інш. – К.: КНЕУ, 1999.