8.6 Графічний метод розв’язання ігор 2nіm 2.

Пояснимо метод на прикладах.

Приклад 8.6. Розглянемо гру, що задана платіжною матрицею

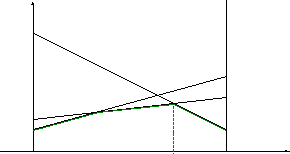
На площині хОy введемо систему координат і на осі Ох відкладемо відрізок одиничної довжини А₁, А₂, кожній точці якого поставимо у відповідність деяку змішану стратегію гравця 1 (х, 1х) (див. на наведеному ниже рисунку). Зокрема, точці А₁ (0;0) відповідає стратегія А₁, а точці А₂ (1;0) – стратегія А₂ і т.д.

y

B₃

11

B₁

7

B₂

B₂

5

B₃

М N

3

B₁

A₁

A₂

2  2

0

x

У точках А₁ і А₂ відновимо перпендикуляр, на яких будемо відкладати виграші гравців. На першому перпендикулярі (у даному випадку він збігається з віссю 0y) відкладемо виграш гравця 1 при стратегії А₁, а на другому – при стратегії А₂. Якщо гравець 1 застосує стратегію А₁, то виграє при стратегії В₁ гравця 2 – 2 у.о., при стратегії В₂ – 3 у.о., а при стратегії В₃ – 11у.о.. Числам 2, 3, 11 на вісі 0х відповідають точки В₁, В₂ і В₃. Якщо ж гравець 1 застосує стратегію А₂, то його виграш при стратегії В₁ дорівнює 7 у.о., при В₂ – 5 у.о., а при В₃ – 2 у.о.. Ці числа визначають точки В₁, В₂, В₃ на перпендикулярі, відновленому в точці А₂.

З'єднуючи між собою точки В₁ і В₁, В₂ і В₂, В₃ і В₃ отримаємо три прямі, відстань до яких від осі 0х визначає середній виграш при будь-якому поєднані відповідних стратегій. Наприклад, відстань від будь-якої точки відрізка В₁В₁ до осі 0х визначає середній виграш ₁ при будь-якому поєднані стратегій А₁ А₂ (з частотами х і 1–х) і стратегією В₁ гравця 2. Ця відстань дорівнює

2х₁ + 6(1  х₂) = ₁ .

(Згадаєте планіметрію і розглянете трапецію А₁ B₁ B₁ A₂). Таким чином, ординати точок, що належать ламаної В₁ M  В₃ визначають мінімальний виграш гравця 1 при застосуванні їм будь-яких змішаних стратегій. Ця мінімальна величина є максимальною в точці . Отже цій точці відповідає оптимальна стратегія Х* = (х, 1х), а її ордината дорівнює ціні гри . Координати точки  знаходимо як точку перетинання прямих В₂ B₂ і В₃ B₃. Відповідні два рівняння мають вигляд

.

Отже Х = (3/11; 9/11), при ціні гри  = 49/11. Таким чином, ми можемо знайти оптимальну стратегію за допомогою матриці .

Оптимальні стратегії для гравця 2 можна знайти із системи

і, отже, Y = (0; 9/11; 2/11). (З рисунка видно, що стратегія B₁ не ввійде в оптимальну стратегію.

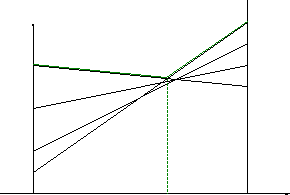
Приклад 8.7. Розв’яжемо гру, задану матрицею

.

A₄

x 8

A₃

7

A₁

A₂

6 К 6

A₁

A₂

5

4

A₃



2

A₄

1

N y

B₂

B₁

Розв’язання. Матриця має розмірність 2 ^х 4. Будуємо прямі, що відповідають стратегіям гравця 1. Ламана А₁ K А₄ відповідає верхній границі виграшу гравця 1, а відрізок  –ціні гри. Розв’язок гри, при цьому, такий

 = (;);Х = (; 0; 0;);  = .