Розділ 10. Безкоаліційні ігри

Антагоністичні ігри, що розглядалися вище, описують конфлікти досить часткового виду. Більш того, реально для більшості конфліктів антагоністичні ігри або зовсім не можуть вважатися прийнятними, або можуть розглядатися як грубі наближення. По-перше, антагоністичні ігри ніяк не розглядають конфлікти з числом рядків більшим двох. Разом із тим, такі конфлікти не тільки зустрічаються в дійсності, але є принципово складнішими ніж конфлікти з двома учасниками, і, навіть, не піддаються зведенню до останнього. По-друге, навіть у конфліктах з двома учасниками інтереси сторін зовсім не повинні бути протилежними. Часто трапляється так, що одна із ситуацій виявляється більш переважною для обох учасників. По-третє, навіть якщо будь-які дві ситуації порівнюються гравцями за протилежними перевагами, розходження в оцінках цих переваг залишає місце для угод, компромісів і кооперацій. По-четверте, змістовна гострота конфлікту часто не відповідає його формальній антагоністичності. Наприклад, при зустрічі двох бойових одиниць воюючих сторін їх прагнення знищити один одного не є антагоністичним конфліктом: в антагоністичному конфлікті мети сторін строго протилежні, тобто для прагнення однієї сторони знищити іншу протилежним буде прагнення уникнути знищення.

Як приклад бескоалційних ігор (БІ) розглянемо ігри двох осіб з довільною сумою. У скінченій БІ двох гравців кожен з них робить один хід – вибирає одну стратегію з наявних у нього скінченого числа стратегій, і після цього отримує виграш відповідно визначеним для кожного з них матрицями виграшів. Іншими словами такі ігри цілком визначаються двома матрицями виграшів для двох гравців. Тому такі ігри називають біматричними. Нехай у гравця 1 є m стратегій, i =, у гравця 2 єn стратегій, j =. Виграші гравців 1 і 2 відповідно задаються матрицями

А = 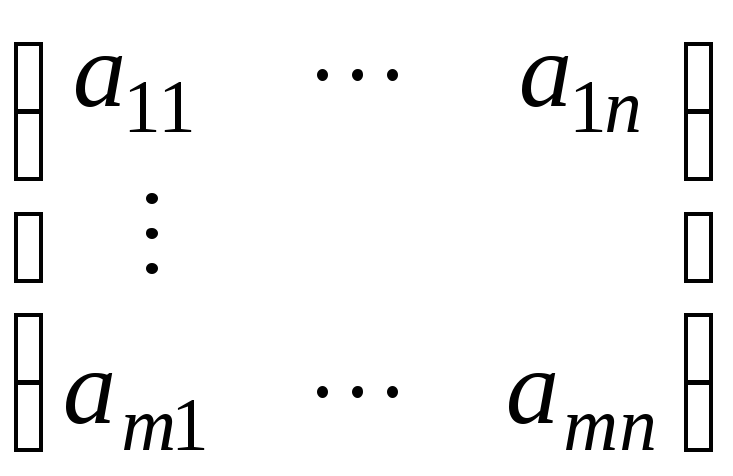,В = .

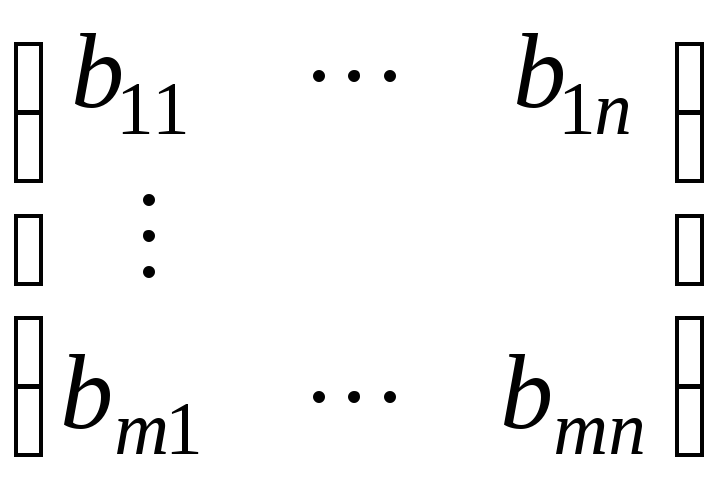Будемо як і раніше вважати повний набір імовірностей x = (x₁, ..., x_m) застосування 1 гравцем своїх чистих стратегій змішаною стратегією гравця 1, і b = (b₁, ..., b_n) – змішаною стратегією гравця 9. тоді середні виграші гравців 1 і 2 відповідно рівні

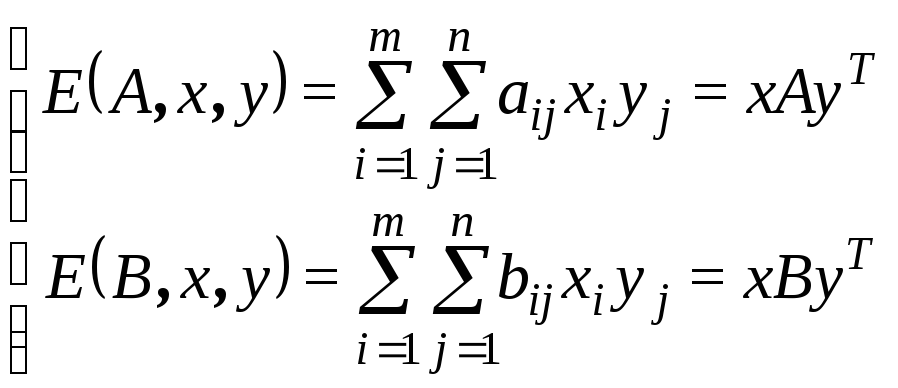(10.1)

Ситуація рівноваги для біматричної гри складає пари (x, y) таких змішаних стратегій гравців 1 і 2, що задовольняють нерівностям :

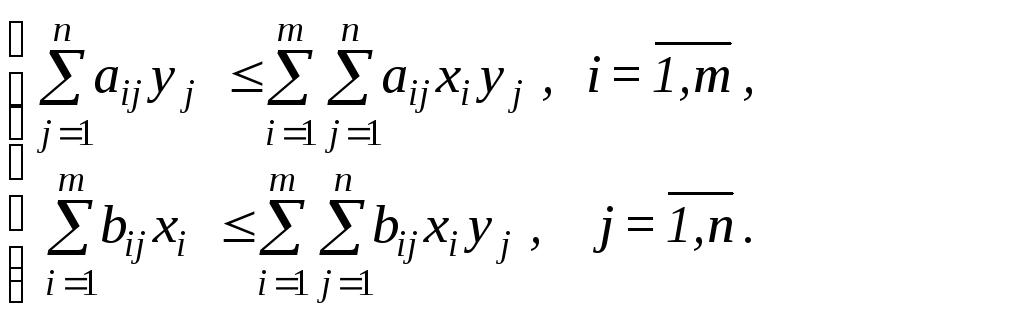(10.2)

або

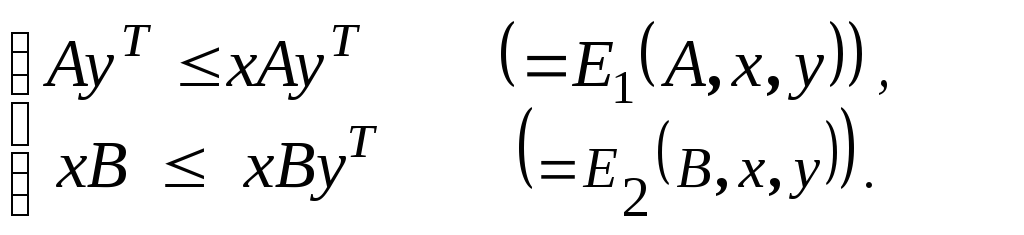(10.3)

Для визначення ситуацій рівноваги необхідно розв’язати систему нерівностей (10.2) або (10.3) щодо невідомих x = (x₁, ..., x_m) і b = (b₁, ..., b_n) за умов

, ,x_i ³ 0 (i =),y_j ³ 0 (j =).

Теорема 10.1. (Нэша). Кожна біматричная гра має принаймні одну ситуацію рівноваги.

Як приклад розглянемо випадок, коли кожен гравець має дві чисті стратегії. У цьому випадку матриці A і B рівні:

A = 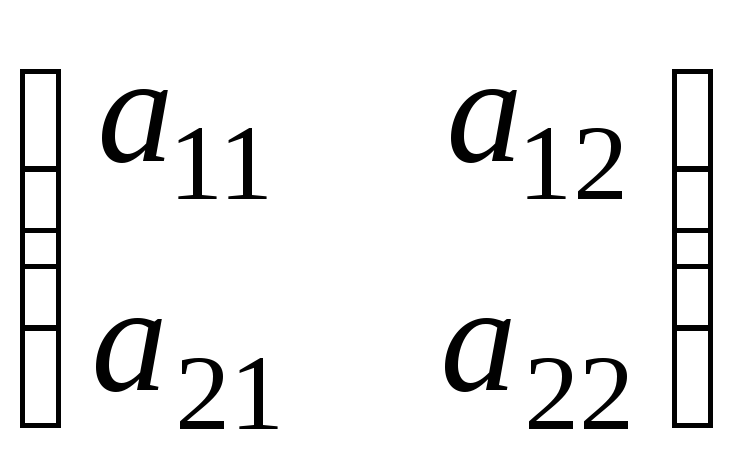,B = .

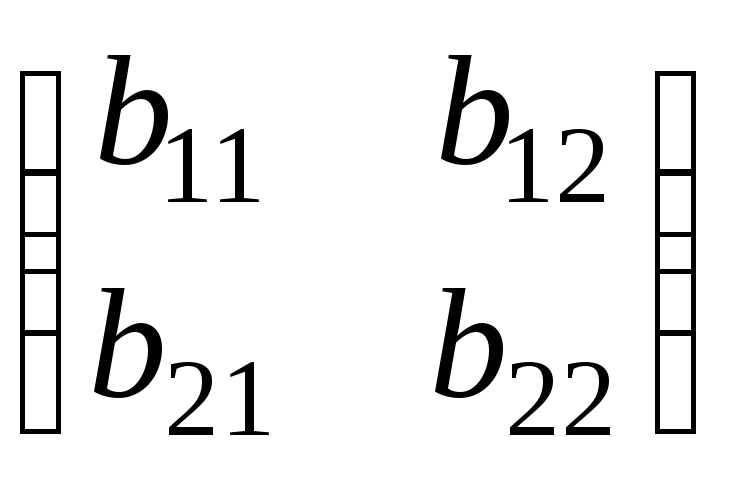Змішані стратегії для гравців 1 і 2 мають вигляд:

(x, 1– x); (y, 1– y); 0 £ x £ 1; 0 £ y £ 1,

а середні виграші рівні :

E₁(A,x,y) = xA = (x; 1- x)=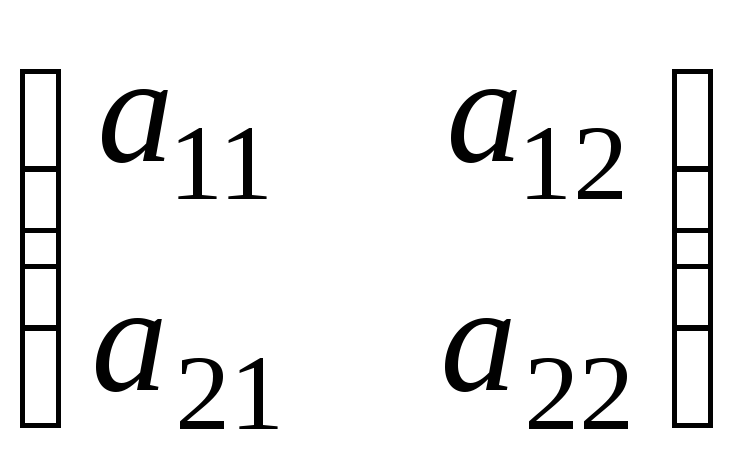

= (a₁₁ – a₁₂ – a₂₁ + a₂₂) xy + (a₁₂ - a₂₂) x + (a₂₁ - a₂₂) y + a_29.

E₂(B,x,y) = xB = (x; 1- x)=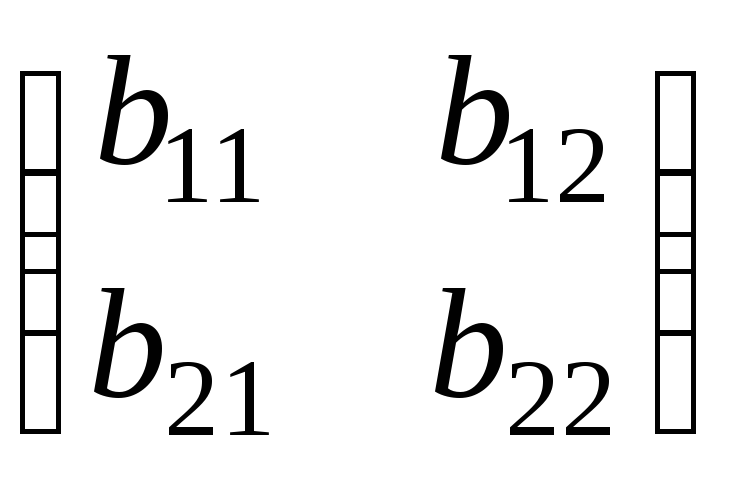

= (b₁₁ - b₁₂ - b₂₁ + b₂₂) xy + (b₁₂ - b₂₂) x + (b₂₁ - b₂₂) y + b_29.

Умови (10.2) будуть виглядати як:

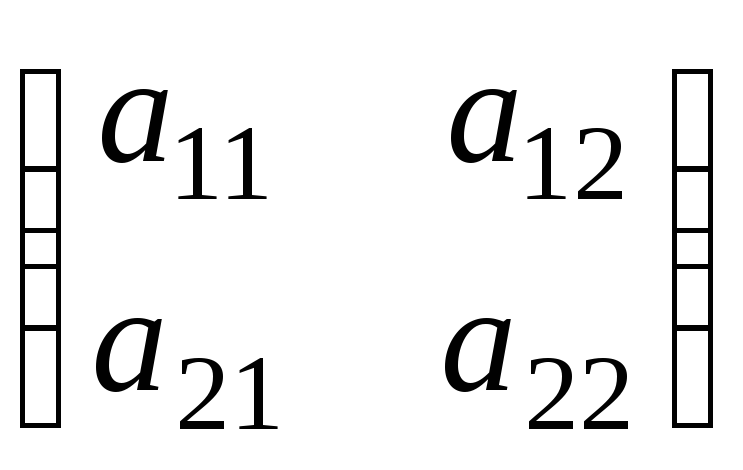
£ E₁(A,x,y),

(x; 1- x)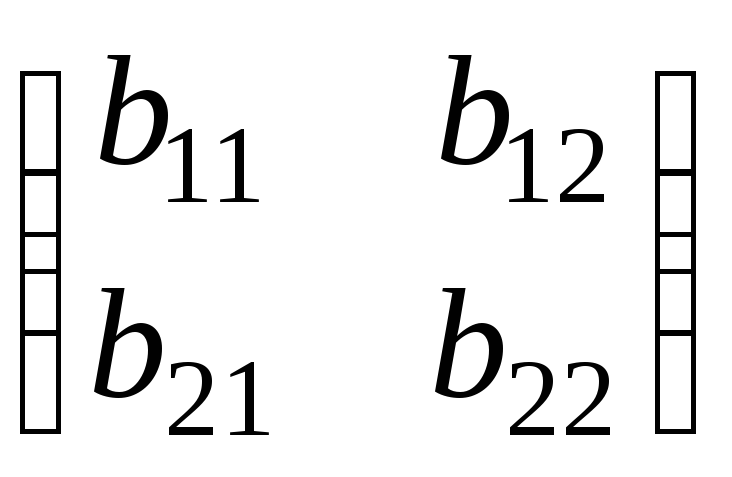£ E₂(B,x,y),

або

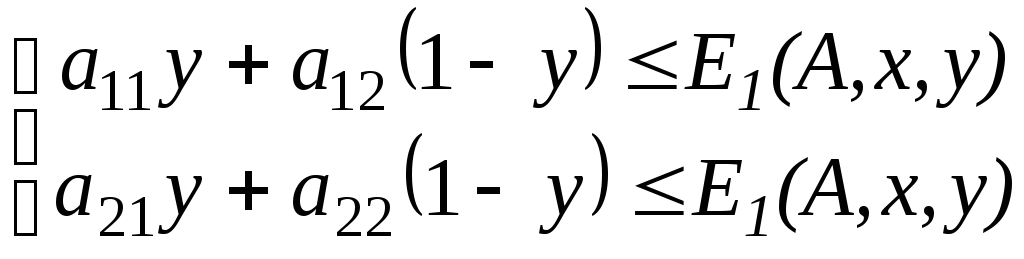(10.4)

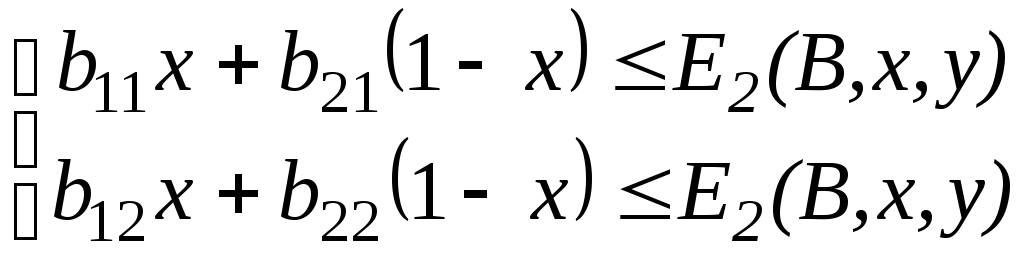(10.5)

Перетворивши (10.4) і (10.5), отримаємо

(1- x) y + (1- x) £ 0

(a₁₁ - a₁₂ - a₂₁ + a₂₂) xy + (a₁₂ - a₂₂) x ³ 0

або

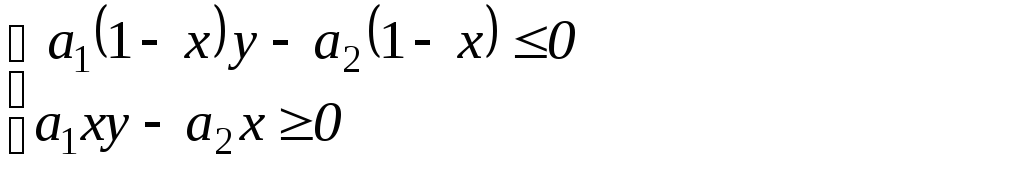(10.6)

Таким чином множина прийнятних стратегій для гравця 1 задовольняє умовам (10.6), 0 £ x £ 1; 0 £ y £ 1. Щоб знайти x розглянемо 3 випадки:

1. Якщо x = 0, то (10.6) справедливо " y, а його верхня нерівність буде мати вигляд:

a₁y - a₂ £ 0. (10.7)

9. Якщо x = 1, то (10.6) справедливо " y, а його верхня нерівність буде мати вигляд:

a₁y - a₂ ³ 0. (10.8)

10. Якщо 0 < x < 1, то верхню нерівність (10.6) розділимо на (1 - x), а нижню нерівність (10.6) – на x. У результаті отримаємо

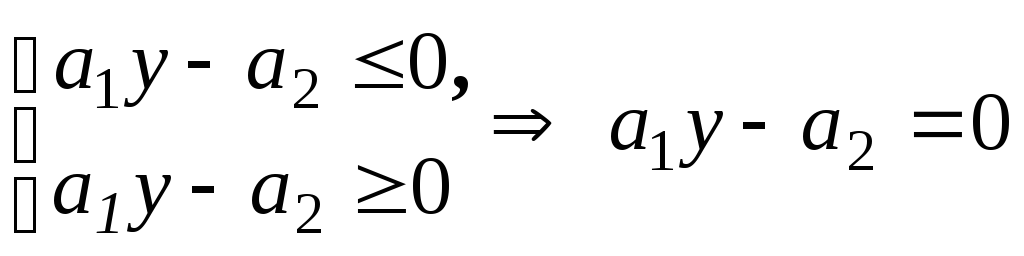(10.9)

Отже, множина К розв’язків системи (10.6) складається з:

• усіх ситуацій виду (0; y), якщо a₁y - a₂ £ 0; 0 £ y £ 1;

• усіх ситуацій виду (x; y), якщо a₁y - a₂ = 0; 0 < x < 1;

• усіх ситуацій виду (1; y), якщо a₁y - a₂ ³ 0; 0 £ y £ 1.

Якщо a₁ = a₂ = 0, то розв’язком є xÎ[0; 1], yÎ[0; 1], оскільки всі нерівності (10.7) – (10.8) виконуються для всіх x і y, тобто множина прийнятних для гравця 1 ситуацій покриває весь одиничний квадрат.

Якщо a₁ = 0, a₂ ¹ 0, то виконується або (10.7), або (10.8), і тому розв’яз­ком є або x = 0, або x=1 при 0 £ y £ 1 (прийнятної стратегії в грі не існує).

Якщо a₁ > 0, то з (10.7) отримуємо розв’язок

x = 0; y £ a₂/a₁:= a.

З (10.8) випливає ще розв’язок визначиться як

x = 1, y ³ a,

а з (10.9) – як

0 < x < 1, y = a.

Якщо a₁ < 0, то розв’язок буде таким:

x = 0, y ³ a; x = 1, y £ a; 0 < x < 1, y = a.

При цьому необхідно враховувати, що додатково повинно виконуватись умова 0 £ y £ 1.

Геометрично це виглядає такий чином:

y ¥ y ¥ y ¥

1 1 1

a₁>0 a₁>0 a₁>0

a<0 a=0 (x, a) 1< a<1

0 1 x 0 1 x 0 1 x

– ¥ – ¥ – ¥

y ¥ y y

¥ ¥

1 a₁>0 1 a₁>0 1 a₁< 0

(x, 1) a=1 (0, b) a >1 0< a<1

(x, a)

x x x

0 – ¥ 1 0 – ¥ 1 0 – ¥ 1

Для гравця 2 дослідження аналогічні. Якщо ввести позначення

b₁ := b₁₁ - b₁₂ - b₂₁ + b₂₂

b₂ := b₂₂ -

то множина L прийнятних для нього ситуацій складається з :

• усіх ситуацій виду (x, 0), якщо b₁x - b₂ < 0; 0 £ x £ 1,

• усіх ситуацій виду (x, y), якщо b₁x - b₂ = 0; 0 £ x £ 1; 0 < y < 1,

• усіх ситуацій виду (x, 1), якщо b₁x - b₂ > 0; 0 £ x £ 1.

При цьому, результати будуть такими:

• якщо b₁ = b₂ = 0, то розв’язок 0 £ x £ 1; 0 £ y £ 1;

• якщо b₁ = 0; b₂ ¹ 0, то розв’язок або y = 0, або y = 1 при 0 £ x £ 1 (прийнятної стратегії в грі не існує);

• якщо b₁ > 0, то y = 0, x < b₂/b₁= b; y = 1, x > b; 0 < y < 1; x = b;

• якщо b₁ < 0, то y = 0, x > b; y = 1, x < b; 0 < y < 1; x = b

При цьому необхідно враховувати, що 0 £ x £ 1.

Геометрично це виглядає такий чином:

y y

1 1

(b,y) (b,y)

x x

0 1 0 1

b₁ > 0 b₁ < 0

0 < b < 1 0 < b < 1

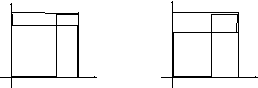
Розв’язком гри є перетинання множин K і L, тобто ті значення x і y, що є загальними для множин K і L.

y y

1 1

x x

0 1 0 1

а) б)

При цьому зиґзаґи K і L можуть бути не тільки однакової, але і протилежної спрямованості. У першому випадку зиґзаґи мають одну точку перетинання, а в-другому ­­­– три. Середні виграші при цьому визначаються по формулах (10.1), якщо в них підставити отримане розв’язок x і y (рис.а). Очевидно a входить у змішану стратегію гравця 2, хоча залежить тільки від виграшів 1 гравця; b входить у змішану стратегію гравця 1, хоча залежить тільки від виграшів гравця 9.

Порівняння цих результатів з результатами розв’язку матричних ігор з нульовою сумою показує, що a збігається з оптимальною стратегією гравця 1 у матричній грі з матрицею A, а b – з оптимальною стратегією гравця 2 у матричній грі з матрицею B. Звідси можна зробити висновок, що рівноважна ситуація направляє поводження гравців не тільки на максимізацію свого виграшу, скільки на мінімізацію виграшу супротивника.

З іншого боку, природно також розглядати поводження гравців у безкоаліційних іграх, спрямоване на максимізацію свого виграшу з урахуванням максимальної протидії гравця, тобто найкращою стратегією гравця 1 вважати оптимальну змішану стратегію гравця 1 у грі з матрицею A, а найкращою стратегією гравця 2 вважати оптимальну змішану стратегію гравця 2 у грі з матрицею B, якщо в ній шукати розв’язок с позицій максимізації виграшу гравця 2, тобто розв’язувати її, як для гравця 1, з матрицею .

Приклад 10.1. Міністерство хоче побудувати один з двох об'єктів на території міста. Міська влада може прийняти пропозицію міністерства або відмовити. Міністерство – гравець 1 – має дві стратегії: будувати об'єкт 1 і будувати об'єкт 9. Місто – гравець 2 – має дві стратегії: прийняти пропозицію міністерства або відмовити.

Свої дії (стратегії) вони застосовують незалежно один від одного, і результати визначаються прибутком (виграшем) відповідно до таких матриць:

A = ,B =

(наприклад: якщо гравці застосовують свої перші стратегії, міністерство вирішує будувати 1 об'єкт, а міські влади дозволяють його будівлю, тоді місто отримує виграш 5 млн у.о., а міністерство втрачає 10 млн у.о., і т.д.)

Розв’язання. Для цієї гри маємо:

a₁ = a₁₁ - a₁₂ - a₂₁ + a₂₂ = -10 - 2 - 1 - 1 = -14 < 0,

a₂ = a₂₂ - a₁₂ = -1 - 2 = -3,

.

Оскільки a₁ < 0, то множина розв’язків K має такий вигляд :

(0, y) при 3/14; (x, 3/14) при 0 £ x £ 1; (1, y) при 0 £ y £ 3/14.

Для другого гравця маємо:

b₁ = b₁₁ - b₁₂ - b₂₁ + b₂₂ = 5 + 2 + 1 + 1 = 9 > 0,

b₂ = b₂₂ - b₂₁ = 1 + 1 = 2,

.

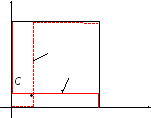
Оскільки b₁ > 0, множина розв’язків має такий вигляд:

1

(x; 0), при 0 £ x £;

(;y), при 0 £ y £ 1; L

(x; 1), при £ x £ 1. K

0 1x

Точкою перетинання множин L і K є точка C з координатами x = 2/9; y = 3/14 і є відповідно прийнятними стратегіями міністерства і міста. При цьому виграш відповідно дорівнює

E₁(A,x,y) = (x, 1-x)==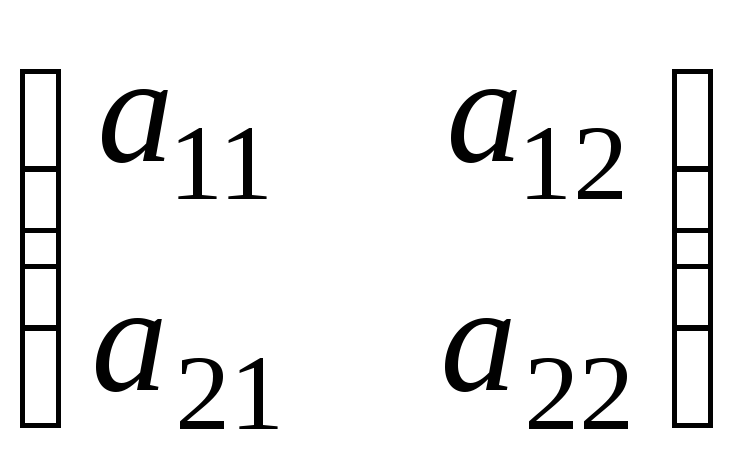

E₂(A,x,y) = (x, 1-x)=

Зауваження. Якщо розв’язати цю гру як матричну гру двох гравців з нульовою сумою, то для гри з матрицею A оптимальні змішані стратегії для гравця 1 і ціна ігри виходять з розв’язку рівнянь

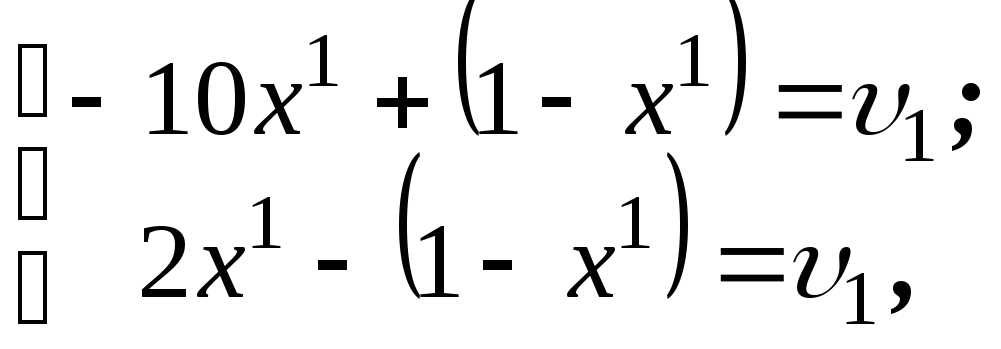
звідки ймовірність застосування гравцем 1 першої стратегії дорівнює , ціна гри– , що збігається зE₁. Ймовірність застосування гравцем 2 першої стратегії ; для гри з матрицеюB оптимальні змішані стратегії і ціна гри для гравця 2 визначаються із системи :

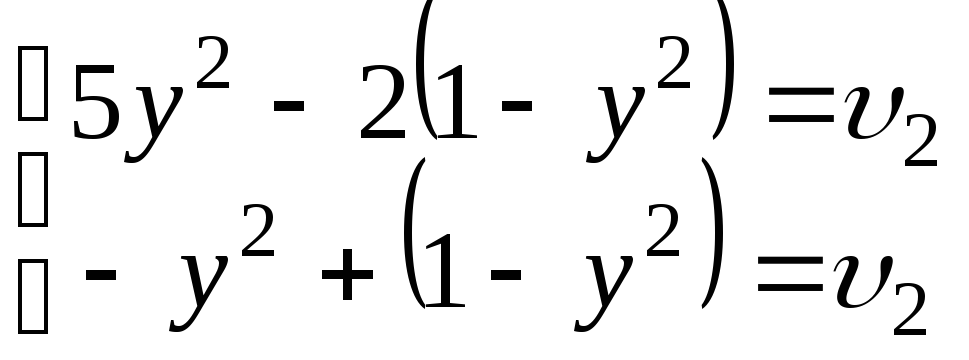
Отже, ймовірність застосування другим гравцем свої стратегії буде визначатися як , а першим гравцем -, ціна гри, при цьому, буде дорівнювати, що збігається зE_9.

Таким чином, якщо кожний із гравців буде застосовувати свої стратегії в цій грі, виходячи тільки з матриць своїх виграшів, тj їхні оптимальні середні виграші збігаються з їх виграшами при ситуації рівноваги.