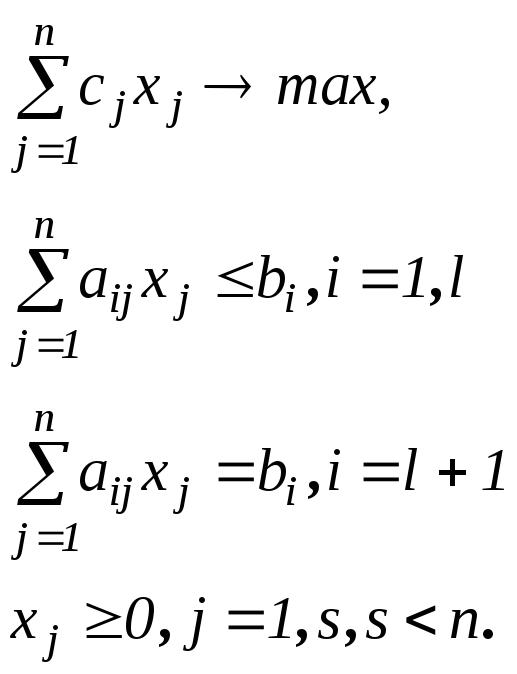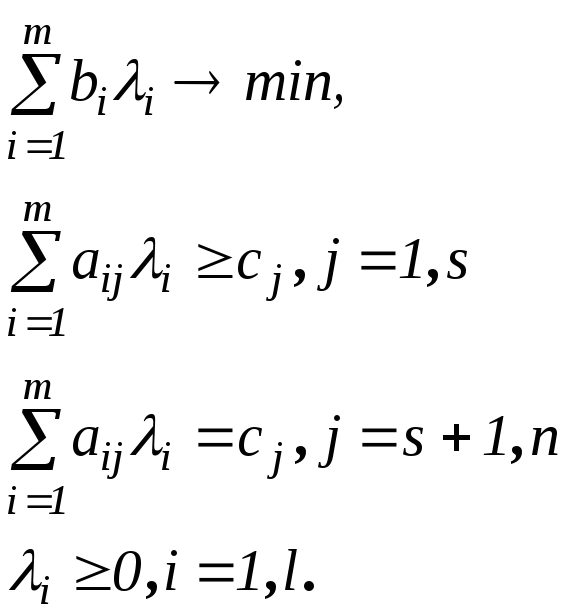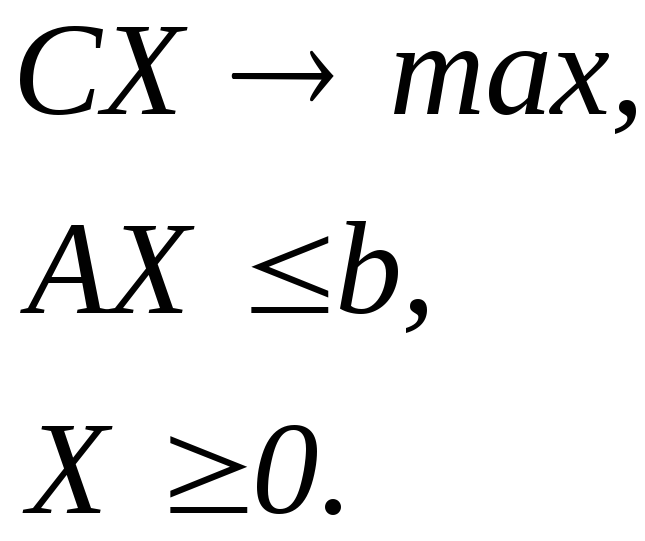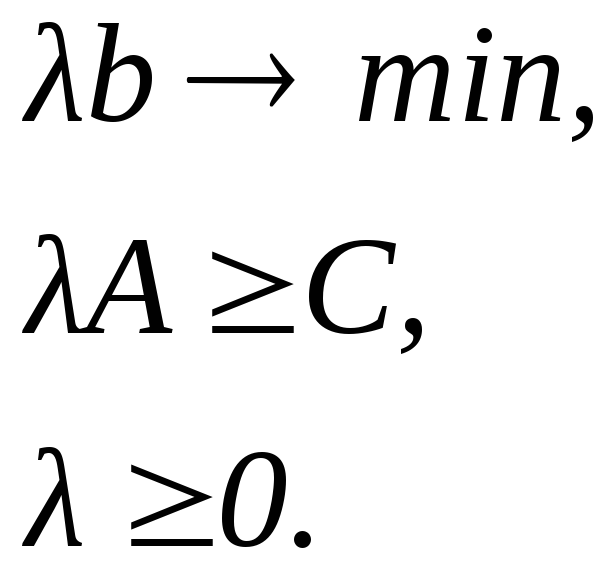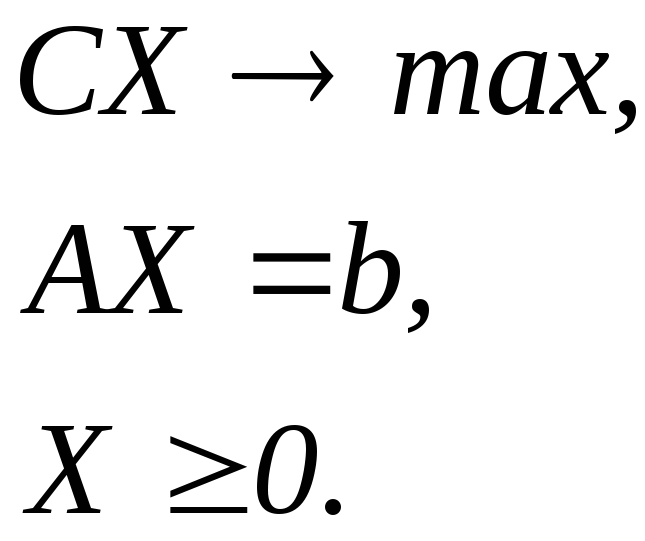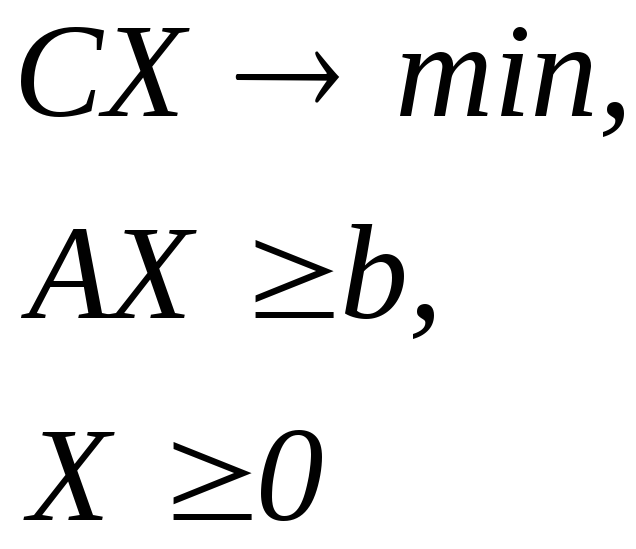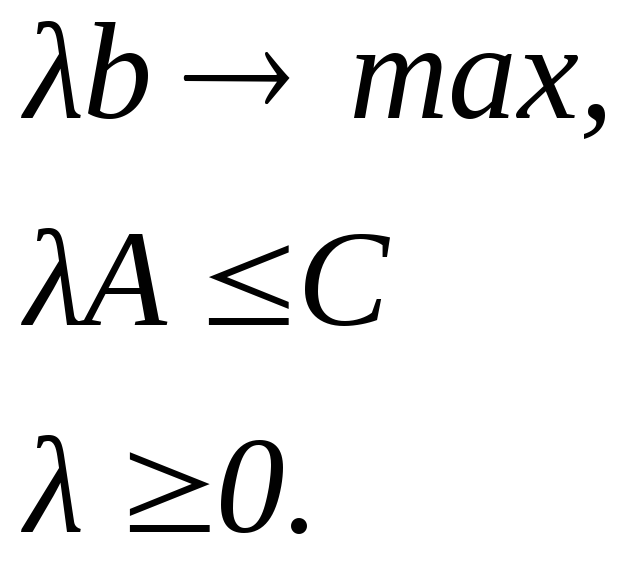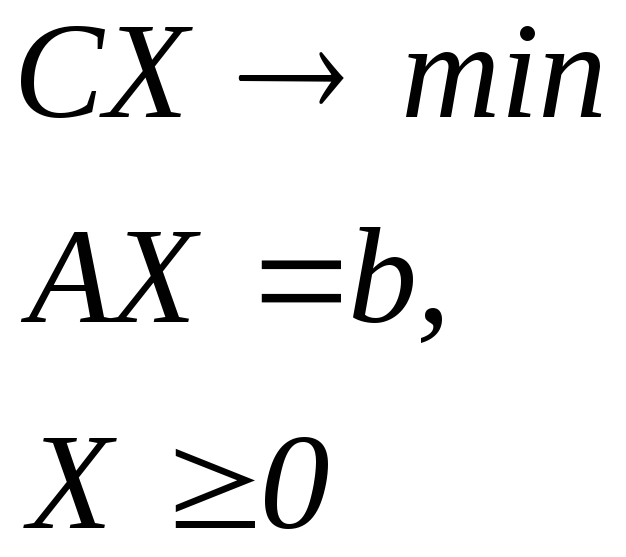2.7 Метод штучної бази

Для отримання системи в канонічному вигляді, що має припустимий базисний розв’язок, існує також і спеціальний метод. Спочатку задача ЛП приводиться до стандартної форми, у якій усі змінні додатні. Потім для кожного обмеження перевіряється існування відповідної базисної змінної. Якщо її не має, то вводиться нова штучна змінна, що відіграє роль базисної для даного обмеження. Після перевірки усіх обмежень отримується система у канонічному вигляді і з'являється можливість заповнити початкову симплексну таблицю. Оскільки введені змінні не мають відношення до суті задачі ЛП у вихідній постановці, то необхідно досягти обертання в нуль штучних змінних. Це можна зробити за допомогою двох-етапного симплекс-методу.

Етап 1. Розглядається штучна цільова функція, що дорівнює сумі штучних змінних, яка мінімізується за допомогою симплекс-методу. Іншими словами, здійснюється виключення штучних змінних. Якщо мінімальне значення допоміжної задачі дорівнює нулю, то всі штучні змінні обертаються в нуль і отримується припустимий базисний розв’язок початкової задачі. Далі реалізується етап 2. Якщо мінімальне значення допоміжної задачі позитивне, то принаймні одна з штучних змінних також позитивна, що свідчить про суперечливість початкової задачі, і обчислення припиняються.

Етап 2. Припустимий базисний розв’язок, що знайдений на першому етапі, поліпшується щодо цільової функції вихідної задачі на основі симплекс-методу, тобто оптимальна таблиця першого етапу стає початковою таблицею другого і змінюється цільова функція.

Зауваження до симплекс-методу.

1. Якщо у ведучому стовпці немає жодного строго додатного елементу, то задача не має оптимального розв’язку, а цільова функція необмежена знизу (у задачі на мінімум) або необмежена зверху (у задачі на максимум).

2. Якщо в останній таблиці оцінка будь-якої небазисної змінної дорівнює нулю, то задача, має нескінченну множину оптимальних розв’язків.

3. Слабкі змінні зі знаком " + ", що вводяться для канонізації нерівностей можна використовувати як базисні.

4. Допустимий базисний розв’язок, в якому одна або кілька базисних змінних дорівнюють нулю, називається виродженим. Поява такого розв’яз­ку може призвести до зациклення. Для виходу із зациклення під час визначення ведучого рядка замість елементів слід перебирати елементи стовпчиків до тих пір поки ведучий рядок не буде визначений однозначно.

2.8 Двоїсті (спряжені) задачі лінійного програмування

Модель пари двоїстих задач у загальній формі. В загальному випадку для кожної задачі ЛП у загальній формі запису можна поставити у відповідність двоїсту (спряжену) для неї задачу (табл.2.6, 2.7).

Таблиця 2.6

Вихідна задача ЛП	Спряжена задача ЛП

Таблиця 2.7

Моделі спряжених задач
Симетричні моделі		Несиметричні моделі
Вихідна	Спряжена	Вихідна	Спряжена

Правила формування двоїстих задач формулюються таким чином.

1. Одна з двох спряжених задач є задачею пошуку максимуму лінійної форми, а друга - мінімуму лінійної форми.

2. Матрицю обмежень спряженої задачі визначають шляхом тран­спонування матриці вихідної задачі.

3. Коефіцієнти лінійної форми спряженої задачі є вільними членами системи обмежень вихідної задачі.

4. Вільні члени системи обмежень спряженої задачі є коефіцієнтами лінійної форми вихідної задачі.

5. Кожній змінній прямої задачі відповідає одне обмеження спряженої задачі, причому якщо j-а змінна невід’ємна, то j-им обмеженням спряженої задачі буде нерівність із знаком  (не менше) і навпаки; змінним, які не мають обмеження на знак, відповідають обмеження рівності.

6. Кожному обмеженню прямої задачі відповідає одна змінна спря­женої задачі, причому, якщо і-е обмеження нерівністю типу  (не більше), то і-а змінна спряженої задачі – невід’ємна; обмеженням у вигляді рівностей відповідають змінні без обмеження на знак.

У загальному випадку розрізняють симетричні і несиметричні двоїсті задачі, відповідні моделі яких наведено у табл. 2.7.

Основні теореми двоїстості. Властивості основної теореми двоїстості можна описати у вигляді таблиці (табл. 2.8).

Таблиця 2.8

Двоїста задача	Пряма задача
	Має плани	Немає планів
Має плани	max F(x)=min G()	min G()
Немає планів	Max F(x)	Можливо

Друга теорема двоїстості надає властивості оптимальних планів парі спряжених задач (умови доповняльної нежорсткості):

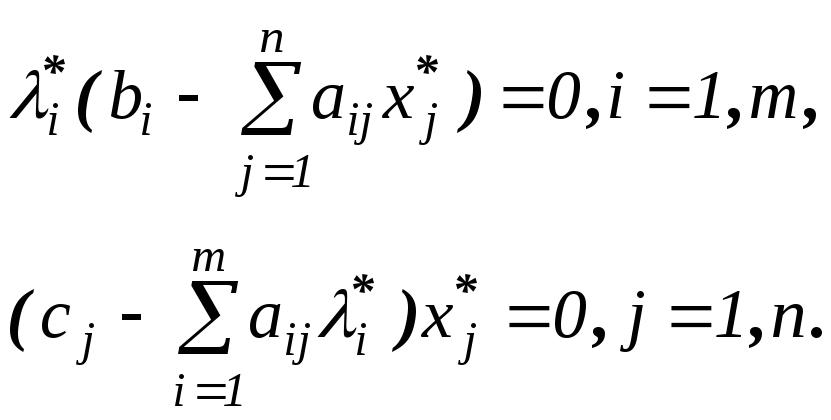
Розв’язавши одну з пари симетричних задач, можна за значеннями в (m+1)-му рядку кінцевої симплекс-таблиці визначити значення змінних оптимального плану другої задачі. Оптимальні значення змінних двоїстої задачі знаходять із співвідношень:

Наприклад, у задачі

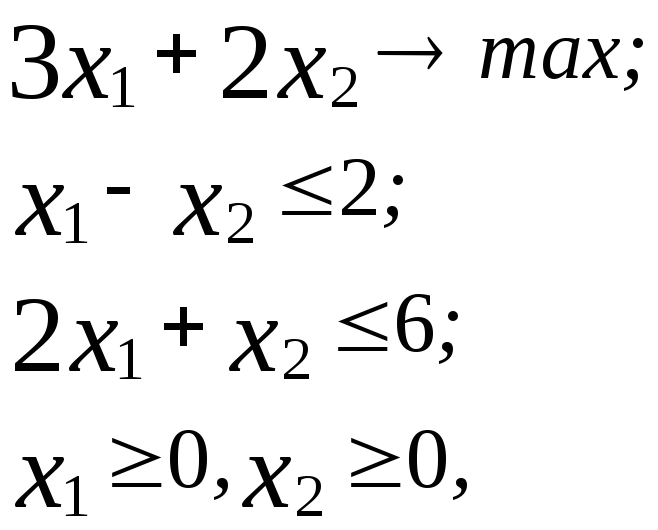
розв’язок якої наведено у таблиці нижче, з останньої таблиці знаходимо, що .Аналогічно з індексного рядка кінцевої таблиці, що відповідає оптимальному плану двоїстої задачі, маємо, що x_j^*= _m+j^под , j=1,n.

Якщо розглядати несиметричні задачі, то співвідношення для визначення змінних оптимального плану двоїстої задачі набуде вигляду деA^-1_x - матриця, обернена до матриці векторів остан­нього базису. Коли ж ви­хідна задача зведена до одиничного базису, обчислення оберненої матриці не потрібне, бо A^-1_x містить колонки кінцевої таблиці на місці колонок одиничних векторів початкової таблиці.

I	Б	C	X		3	2	0	0
					Р1	Р2	Р3	Р4
1	Р3	0	2		1	-1	1	0
2	Р4	0	6		2	1	0	0
m+1		0			-3	-2	0	0
I	Б	C	X		3	2	0	0
1	Р3	3	2		1	-1	1	0
2	Р4	0	2		0	3	-2	1
m+1		6			0	-5	3	0
I	Б	C	X		3	2	0	0
					Р1	Р2	Р3	Р4
1	Р3	3	8/3		1	0	1	1/3
2	Р4	2	2/3		0	1	-2/3	1/3
m+1		6			0	0	-1/3	5/3
I	Б	C		X	3	2	0	0
					Р1	Р2	Р3	Р4
1	Р3	0		8	3	0	1	1
2	Р4	2		6	2	1	0	2
m+1		6			1	0	0	3

Приклад 2.8. Сформулюємо задачу, двоїсту до такої задачі:

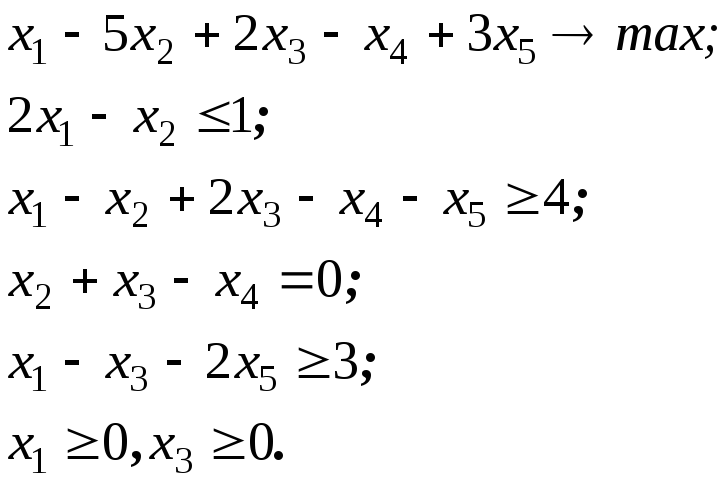
Перепишемо систему обмежень у вигляді

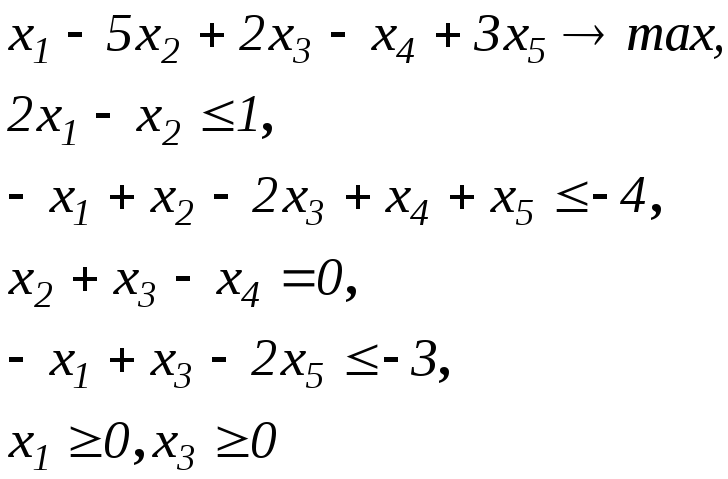
Тоді двоїста задача набуде вигляду

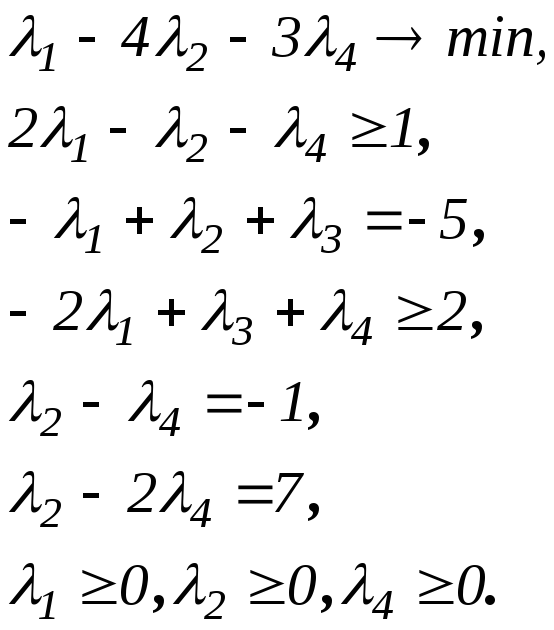
Приклад 2.9. Розв'язати ЗЛП за допомогою геометричної інтерпретації двоїстої задачі:

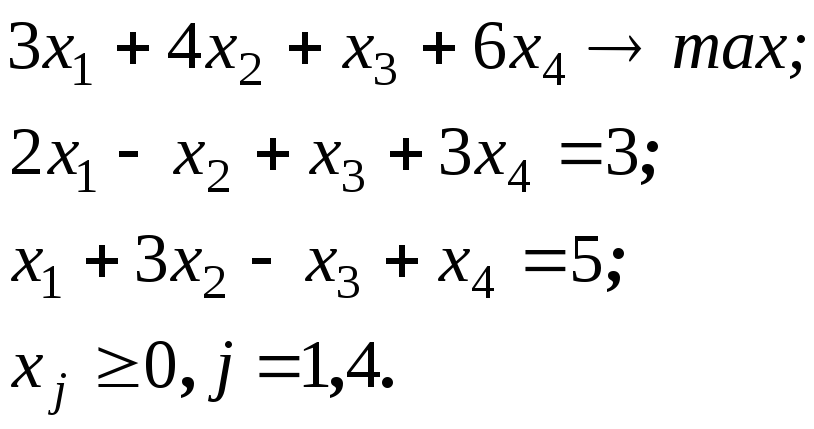
Двоїста їй задача має вигляд:

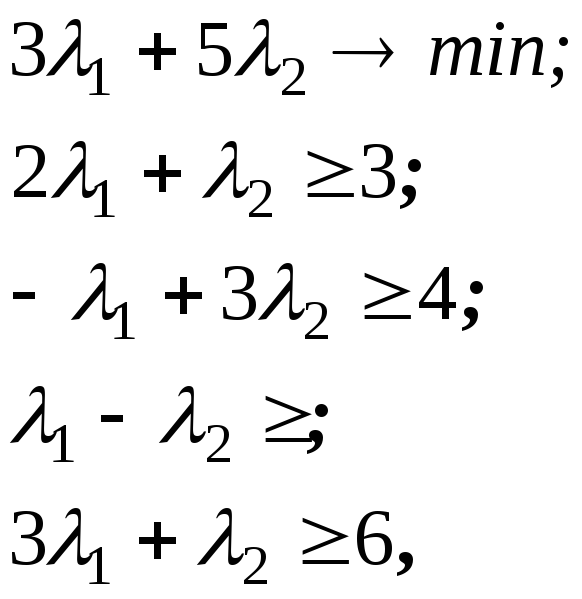
а її геометрична інтерпретація зображена на рисунку нижче.

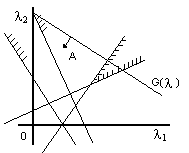
Пряма рівняння G() досягає найменшого значення в точці А, де ^_,^_. Тоді G(^)=23 внаслідок основної теореми F(X^*)=23.

Знайдемо оптимальний план прямої задачі, розглядаючи умови доповняль­ної нежорсткості:

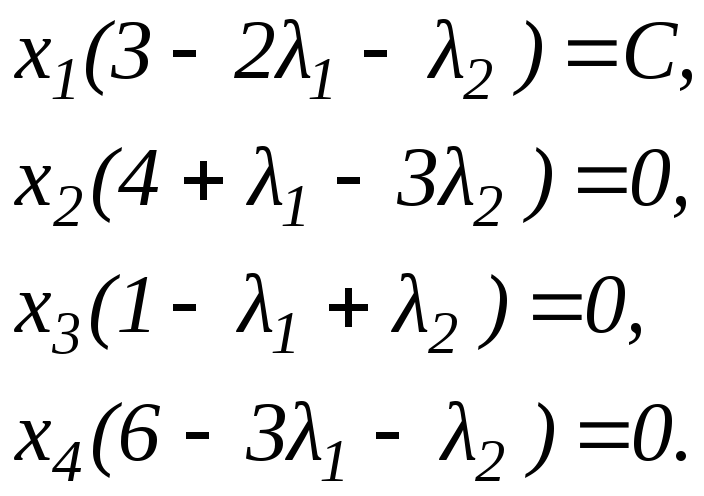
З оптимального плану спряженої задачі маємо, що в другому та третьому співвідношеннях виконується рівність, тоді X₂, X₃, в той час як X₁= 0, X₄=0 оскільки в першому та четвертому співвідно­шеннях рівність не виконується.