8.7 Матричний метод розв’язання ігор

Нехай треба розв’язати гру з платіжною матрицею A = (a_ij)_mn і нехай В - будь-яка квадратна підматриця матриці А , поря­док якої r  2. Тоді алгоритм матричного методу полягає у ви­конанні таких операцій.

І. Вибираємо квадратну підматрицю В матриці А і обчислюємо

,

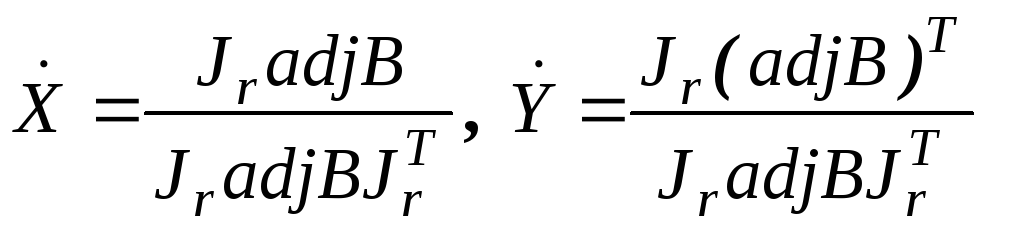де J_r = /1, 1, ..., 1/ - одиничний вектор-рядок; adjB - матриця, приєднана до В; (•)^T - індекс транспонування; - вектор, побудованний зХ викресленням елементів, які відпо­відають рядкам, викресленим з А під час побудови В; – вектор, побудований ізY викресленням елементів, які відпо­відають стовпцям, викресленим з А під час побудови В.

2. Якщо деякі x_i < 0, i =1,r або y_j <0 j =1,r то відкидаємо підматрицю В та спробуємо аналізувати другу.

3. Якщо всі x_i , ir та y_j j =1,r то обчислюємо

4. Будуємо X з таY з , поширюючи ці вектори нулями на тих місцях, де ми викреслювали рядки чи стовпці під час по­будови підматриціВ.

5. Перевіряємо виконанння співвідношень

Якщо хоча б одне з них не виконується, відкидаємо підматриіці і спробуємо аналізувати другу.

Приклад 8.8. Розв’яжемо гру з платіжною матрицею

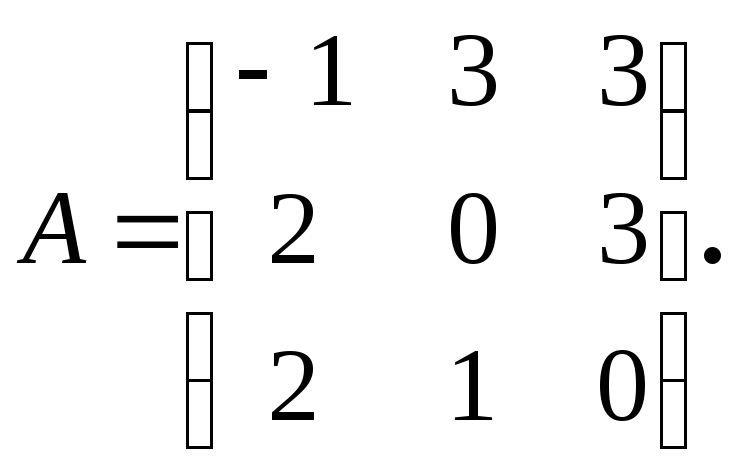
Оскільки матриця А квадратна, то її можна розглядати як підматрицю В, порядок якої r = 3. Тоді

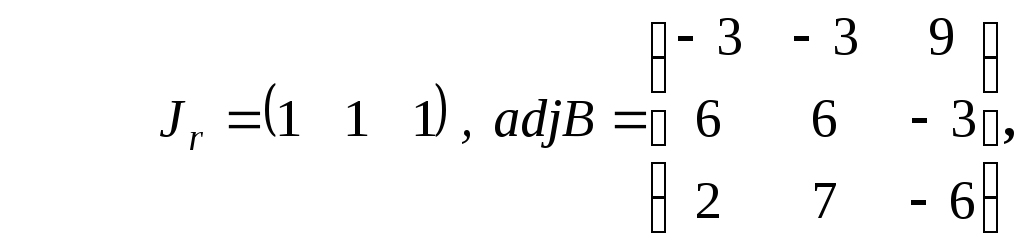
а розв’язок гри, обчислений за наведеними вище формулами, має вигляд

З дев'яти підматриць порядку r=2 лише одна має додатко­вий роз­в’я­зок, а саме для якої

а звідки

Як бачимо, перший гравець має єдину оптимальну стратегію, тоді як другий - множину оптимальних стратегій:

, де

Виникає питання, чи можна зробити вибір між різними оптималь­ними стратегіями. Нехай перший гравець вибирав змішану стратегію Х, а дру­гий - чисту стратегію j. Тоді математичне очікування виграшу першого гравця дорівнює E(X, j).

Змішана стратегія Х домінує змішану стратегію Х’, якщо для кожної чистої стратегії j другого гравця та існує хоча б одна така стратегіяj, для якої Е(Х, j) > Е(Х', j). У такому випадку стратегія Х називається найкращою, якщо вона оптимальна та жодна інша стратегія не домінує її.В розглянутому вище прикладі в другого гравця найкраща страте­гія - це Y= (0, 2/3, 1/3).

8.8. Ітеративні методи розв’язання ігор

^{Зведення матричних ігор до задач лінійного програмування.} Припустимо, що ціна гри додатна ( > 0). Якщо це не так, то відповідно властивості 2.6 завжди можна підібрати таке число с, додаток якого до всіх елементів матриці виграшів дає матрицю з додатними елементами, і отже, з додатними значенням ціни гри. При цьому, оптимальні змішані стратегії обох гравців не змінюються.

Отже, нехай дана матрична гра з матрицею А порядку m n. Відповідно властивості 8.7 оптимальні змішані стратегії х = (х₁, ..., х_m), y = (y₁, ..., y_n) щодо гравців 1 і 2 і ціна гри  повинні задовольняти співвідношенням.

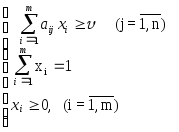(8.7)

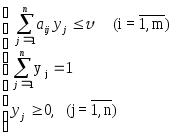(8.8)

Розділимо всі рівняння і нерівності в (8.7) і (8.8) на  (це можна зробити, оскільки за припущенням  > 0) і введемо позначення :

, ,

Тоді (8.7) і (8.8) перепишеться у вигляді :

, ,,,

, ,,.

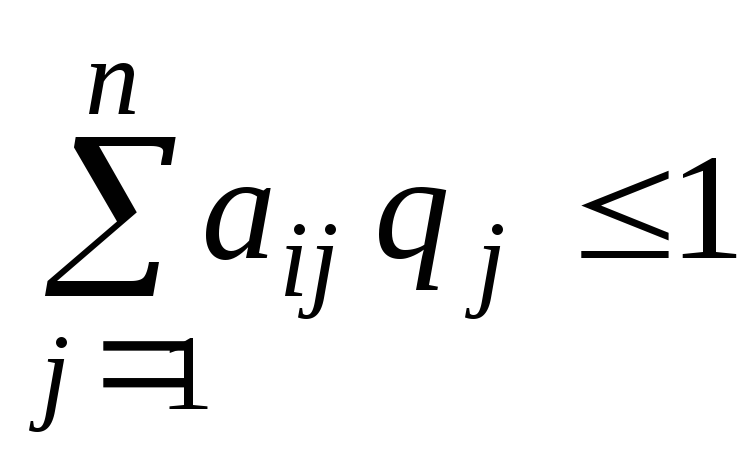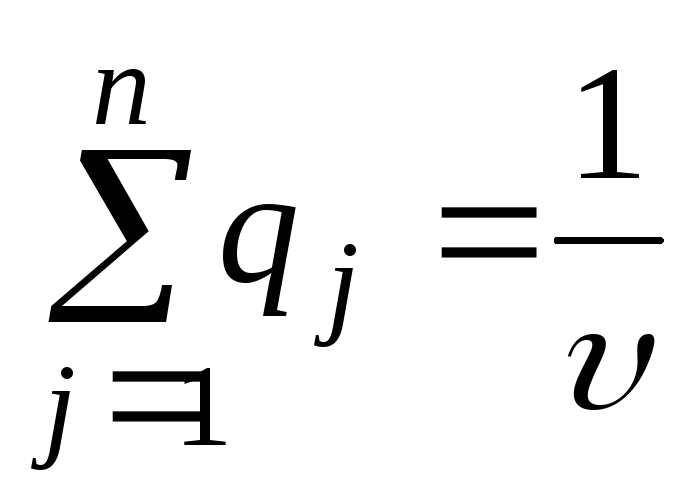Оскільки перший гравець прагне знайти такі значення х_i і, отже, p_i , щоб ціна гри  була максимальною, розв’язок першої задачі зводиться до пошуку таких додатних значень p_i , для яких

, . (8.9)

Оскільки другий гравець прагне знайти такі значення y_j і, отже, q_j, щоб ціна гри  була найменшою, ррохв’язок другої задачі зводиться до пошуку таких додатних значень q_j, , для яких

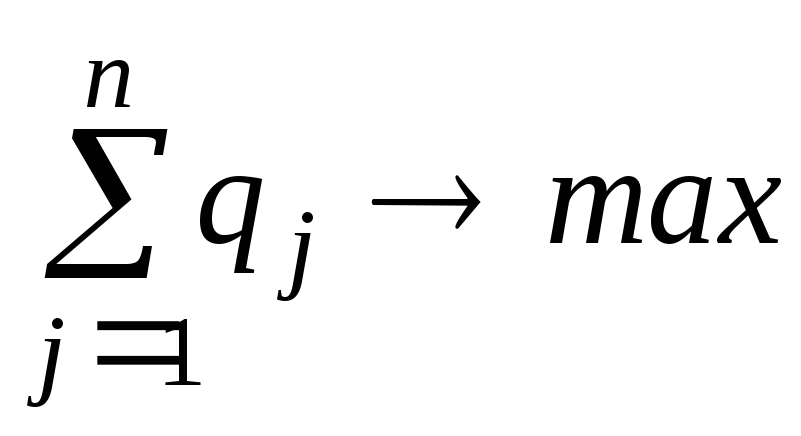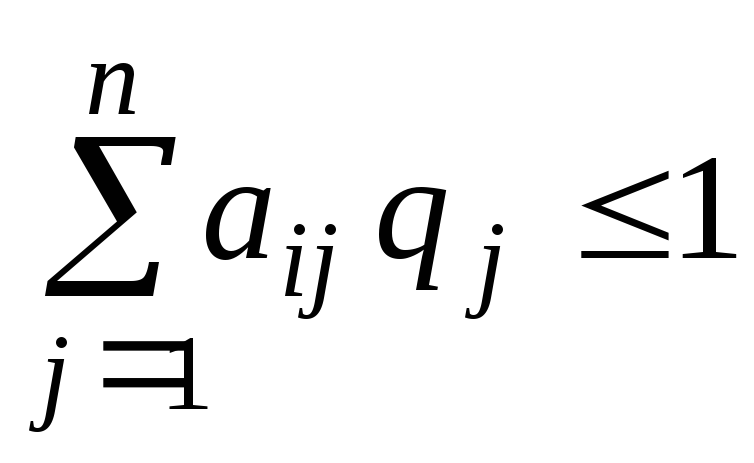, . (8.10)

Формули (8.9) і (8.10) описують двоїсті одна до одної задачі лінійного програмування (ЛП). Розв’язуючи ці задачі, отримаємо значення p_i ,q_j і. Тоді змішані стратегії отримуються за виразами:

. (8.11)

Приклад 8.9. Знайти розв’язок гри, що описується матрицею

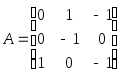
Розв’язання. Під час розв’язання цієї гри до кожного елемента матриці А додамо 1 і отримаємо таку матрицю

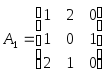
Складемо тепер пару взаємо-двоїстих задач:

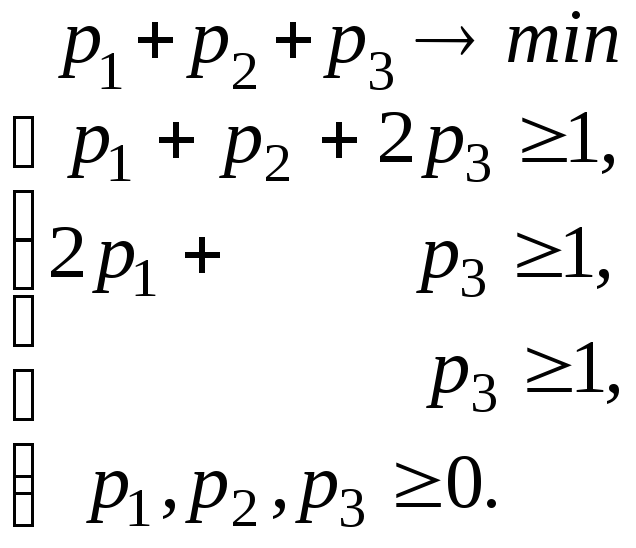
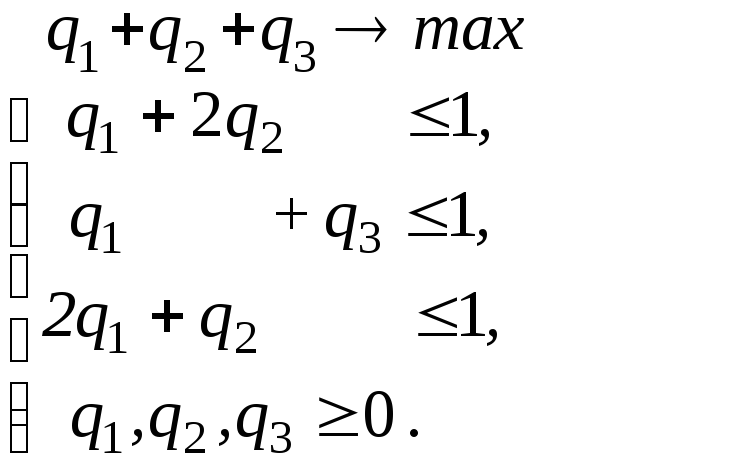
Розв’яжемо другу з них

Б.п.	q1	q2	Q3	q4	q5	q6	Розв’язок		Відношення
	1	1	1	0	0	0	0	3
q4	1	2	0	1	0	0	1	5	—
q5	1	0	1	0	1	0	1	4
q6	2	1	0	0	0	1	1	5	—

Б.п.	q1	Q2	q3	q4	q5	q6	Розв’язок		Відношення
	0	1	0	0	1	0	1	1
q4	1	2	0	1	0	0	1	5
q3	1	0	1	0	1	0	1	4	—
q6	2	1	0	0	0	1	1	5

Б.п.	q1	q2	q3	q4	q5	q6	Розв’язок		Відношення
		0	0		1	0
q2		1	0		0	0
q3	1	0	1	0	1	0	1	4
q6		0	0		0	1

З оптимальної симплекса-таблиці випливає, що

(q₁, q₂, q₃) = (0;; 1),

а із співвідношень подвійності випливає, що

( p₁, p₂, p₃) = (; 1; 0).

Отже, ціна гри з платіжною матрицею А₁ дорівнює

=,

а гри з платіжною матрицею А:

.

При цьому оптимальні стратегії гравців мають вигляд:

Х = (х₁, х₂, х₃) = (р₁; р₂; р₃) = =,

Y = (y₁, y₂, y₃) = (q₁; q₂; q₃) = =.