9.2 Ігри з опуклими функціями виграшів

Ігри з опуклими безперервними функціями виграшів, що називають часто ядром, називаються опуклими.

Нагадаємо, що опуклою функцією f дійсної змінної х на інтервалі (а,b) називається така функція, для якої виконується нерівність

f(a₁ х₁ + a₂ х₂) £ a₁ f(х₁) + a₂ f(х₂),

де х₁ і х₂ – будь-які дві точки з інтервалу (а,b); a₁, a₂ ³ 0, причому

a₁+a₂ = 1.

Якщо для a₁ ¹ 0, a₂ ¹ 0 завжди має місце строга нерівність

f(a₁ х₁ + a₂ х₂) < a₁ f(х₁) + a₂ f(х₂),

то функція f називається строго опуклої на (а;b).

Геометрично опукла функція зображує дугу, графік якої наведено нижче стягуючої її хорди (див. на рисунку нижче).

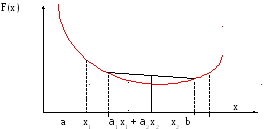
Нагадаємо, також, що безперервна і строго опукла функція f на замкненому інтервалі приймає мінімальне значення тільки в одній точці інтервалу.

Для пошуку розв’язку опуклої гри можна скористатися наступною теоремою.

Теорема 9.4. Нехай М(х, y) – безперервна функція виграшів гравця 1, на одиничному квадраті і строго опукла по y для будь-якого х. Тоді є єдина оптимальна чиста стратегія y = y_o Î[0;1] для гравця 2, ціна гри, при цьому, визначається по формулі

V = M(x, y), (9.1)

значення y_o визначається як рішення наступного рівняння

M(x, y_o) = V. (9.2)

Зауваження. Якщо в теоремі 4 не припускати строгу опуклість функції М(х, y) по y, а просто опуклість, то теорема залишається в силі з тією відмінністю, що в гравця 2 оптимальна чиста стратегія не буде єдиною.

Зауваження. Опуклі ігри називають часто опукло-вгнутими, оскількии в них має сідлообразне ядро, а оскільки ядро сідлообразне, то гра має сідлову точку в чистих стратегіях.

Таким чином, якщо М(х, y) безперервна й опукла по y, то ціна гри визначається за формулою (9.1), і гравець 2 має оптимальну чисту стратегію, обумовлену рівнянням (9.2).

Аналогічно і для гравця 1: якщо функція виграшів М(х, y) безперервна по обох аргументах і строго увігнута по х для будь-якого y, то в цьому випадку гравець 1 має єдину оптимальну стратегію.

Ціна гри визначається за виразом

V = M(x,y), (9.3)

а чиста оптимальна стратегія х_o гравця 1 визначається з рівняння

M(x_o, y) = V. (9.4)

Приклад 9.4. Нехай на квадраті [0;1] задана функція

М(х, y) = . (9.5)

Оскільки дляx Î[0; 1], y Î(0;1), то М(х, y) строго увігнута по х для будь-якого y Î(0;1). Отже, ціна гри знаходиться за виразом (9.3)

V = .

Відзначимо, що при 0 £ х £справедлива рівність

= ,

а при 0,5 < х £ 1

= .

Оскільки

V = max [;] =

= max [;] =max [;] =.

При цьому значення х виходить рівним х_o = . Це ж значення виходить з розв’язку рівняння

= ,

оскільки мінімум досягається при y = 0, і це рівняння перетворюється як

= ,

звідки випливає, що х = .

Помітимо, що якщо у функції виграшів (5) поміняти місцями х и y, те вона не зміниться, а отже, ця функція опукла і по y при всіх х Î[0;1]. Тому до неї застосовна та ж теорія, тобто в гравця 2 існує оптимальна чиста стратегія y_o, обумовлена з рівняння (4)

=

Очевидно, максимум по х досягається при х = 1/2, і останнє рівняння прийме вид

= .

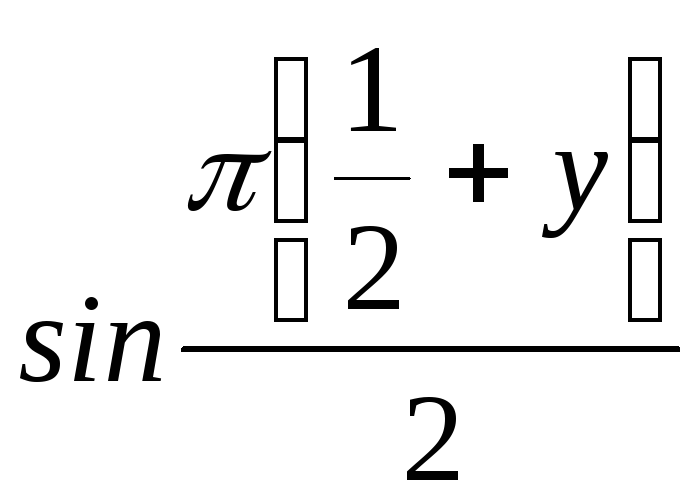Рішенням останнього рівняння буде y_o = 0. Отже, гравець 2 має оптимальну чисту стратегію y_o = 0.

Зауваження. У наведеному вище прикладі ми могли визначити оптимальну стратегію гравця 1, а гравця 2 - тільки випадково, у силу “удалого” виду М(х, y).

Розглянемо тепер метод визначення оптимальних стратегій того гравця, для якого функція виграшів не обов'язково опукла. Нехай безперервна функція М(х, y), задана на одиничному квадраті, опукла по y. Ми буде цікавити питання перебування оптимальних стратегій 1 гравця. Припустимо також, що для х Î[0; 1], y Î[0; 1] існує частинна похідна функції М(х, y) по y, причому в точках y = 0 і y = 1 (х, y) = розглядається як права і ліва похідна відповідно. Позначимо черезy_o одну з оптимальних чистих стратегій гравця 2 (ця стратегія існує відповідно до теореми 9. 4).

Відповідно до теореми 9.2 чисті стратегії х гравця 1 можуть входити в його оптимальну стратегію з позитивною імовірністю, якщо для них виконується рівність М(х, y_o) = V. Такі чисті стратегії х називаються істотними.

Теорема 9.5. Нехай дана нескінченна антагоністична гра з нескінченною і дифференціюємою по y на одиничному квадраті при будь-якому х функцією виграшів М(х, y), з оптимальною чистою стратегією y_o гравця 2 і ціною гри V, тоді :

1) якщо y_o = 1, то серед оптимальних стратегій гравця 1 мається істотна чиста стратегія х₁, для якої

(х₁, 1) £ 1;

2) якщо y_o = 0, то серед оптимальних стратегій гравця 1 є істотна чиста стратегія х₂, для якої

(х₂, 0) ³ 0;

3) якщо 0 £ y_o £ 1, то серед оптимальних стратегій гравця 1 знайдеться така, що є сумішшю двох істотних стратегій х₁ і х_9. Для цих стратегій

(х₁, y_o) £ 0, (х₂, y_o) ³ 0,

стратегія х₁ сумісна з ймовірністю a, стратегія х₂ – з ймовірністю (1 - a), де a знаходиться з рівняння

a(х₁, y_o) + (1 - a)(х₂, y_o) = 0. (9.6)

Приклад 9.5. Нехай функція виграшів у нескінченній антагоністичній грі задана на одиничному квадраті і дорівнює

М(х, y) = (х - y)² = х² - 2хy + y^9.

Ця функція безперервна по х и y, і тому ця гра має рішення. Крім того

= 2 > 0.

Отже, М(х, y) опукла по y, і тому відповідно теореми 9.4 ціна гри визначається за формулою (9.1), гравець 2 має чисту оптимальну стратегію y_o, обумовлену виразом (9.2). Таким чином, маємо

V = (x - y)²;

Для визначення (x² - 2xy + y²) послідовно знайдемо

= 2x - 2y := 0 Þ x = y,

= 2 > 0 Þ при x = y функція M має мінімум для будь-якого y, максимум досягається в одній із крайніх точок x = 0 і (або) x = 1.

M(0; y) = y², M(1; y) = 1 - 2y + y² = (y - 1)² , V=max {y²; (1 - y)²}.

Даний max {...} досягається в тому випадку, якщо y² = (1 - y)², тобто y = 1/9. Отже V = 1/4 при y_o = 1/9.

Визначимо тепер оптимальні стратегії для гравця 1. Оскільки y_o = 1/2, то 0 < y_o < 1. Відповідно до теореми 9.5 розглянемо третій випадок.

Визначимо х з рівняння М(х, y_o) = V, тобто (х -1/2 )² = 1/4.

Розв’язуючи останнє рівняння, отримаємо х₁ = 0, х₂ = 1.

Тепер необхідно визначити величину a – ймовірність застосування чистої стратегії х₁ = 0. Для цього використовуємо рівняння (9.6)

a(0,) + (1- a)(1,) = 0.

Неважко знайти

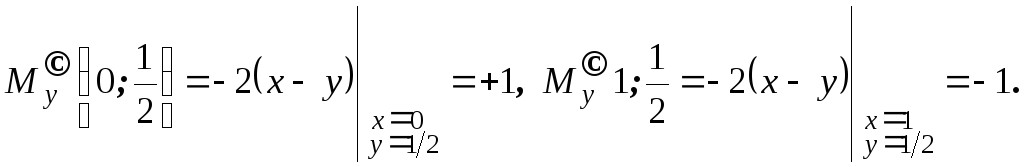
Тоді рівняння для a прийме вигляд: a - (1 - a) = 0, звідки a = 1/2 . Отже, стратегія гравця 1: F(х) = 1/2J_o(х) + 1/2J₁(х), а гравця 2: Q(y) = (y).

Тут через (x) позначена східчаста функція (x) = .