З другої групи умов доповняльної нежорсткості маємо

Оптимальні значення змінних вихідної задачі знайдемо з рівнянь

Тобто, x₂ = 4, x₃ = 7. Оптимальний план вихідної задачі X* = (0, 4, 7, 0); L(X*)= 23.

Приклад 2.10. Критерій оптимальності плану ЗЛП.

Перевірити, чи буде план Х =(0,1,0,3) оптимальним планом для наведеної нижче задачі лінійного програмування.

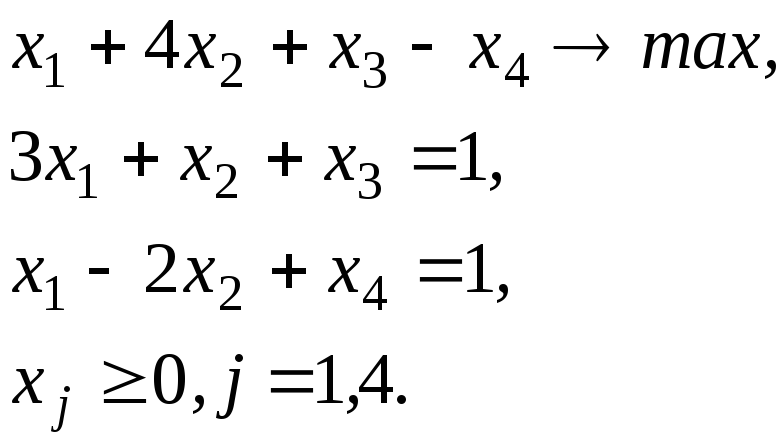
Сформулюємо двоїсту задачу:

₁ +₂  min,

3₁ +₂  1,

₁ –2₂  4,

₁  1, ₂  –1,

Як наслідок другої теореми двоїстості маємо з умов додатності змінних x₂ та x₄, що друге та четверте обмеження двоїстої задачі мають виконуватися як рівності, тобто: Розв’язок цієї системи рівнянь _2_ -1. Він задоволь­няє також перше й третє обмеження-нерівності двоїстої задачі. Умови ж другої теореми повністю задовольняються, що свідчить про оптимальність плану Х.

Розділ 3. Транспортні задачі (т-задачі)

3.1 Математична структура т-задач

Припустимо, що деякий однорідний продукт (вантаж), який зосереджено у m постачальників, по a_i одиниць у кожного (), потрібно перевезтиn споживачам у кількості не менше як b_i одиниць у кожному (). Відома вартість перевезення одиниці вантажу віді-го постачальника до j-го споживача c_ij. Необхідно знайти такий план перевезень продукції від постачальників до споживачів, за яким загальні витрати Z на транспортування були б мінімальними.

Для побудови математичної моделі такої задачі введемо матрицю плану перевезень X = (x_ij), елементи якої означають обсяг перевезень продукції від і-го постачальника до j-го споживача. Тоді для загальних транспортних витрат для обсягу продукції, що вивозиться від кожного поста­чаль­ника і для обсягу продукції, яка надходить до кожного із споживачів можна записати такі вирази:

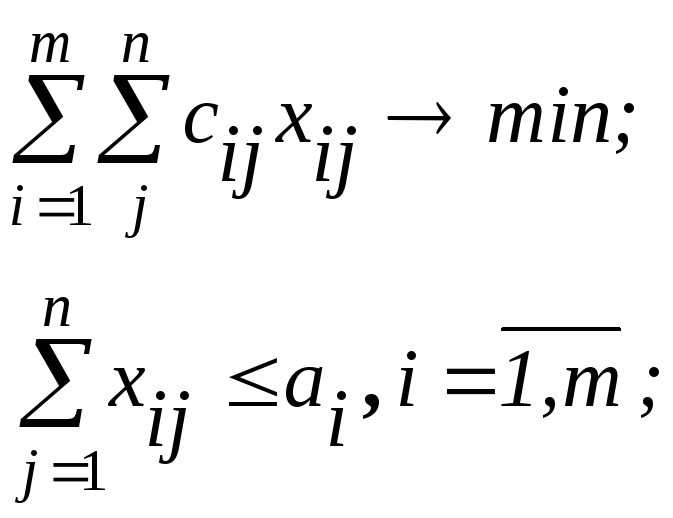
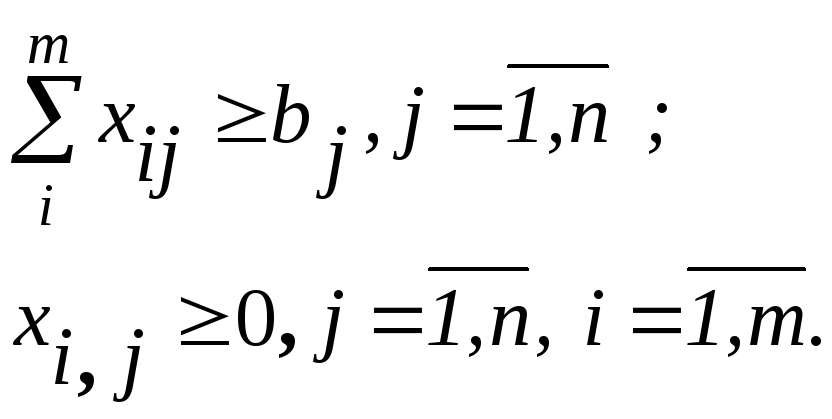
Наведена система формул описує математичну модель класичної транспортної задачі. Згідно з економічним змістом транспортної задачі значення всіх сталих коефіцієнтів моделі, а саме запаси продукції у постачальників, потреби в продукції кожного споживача і транспортні витрати не можуть бути від’ємними, тобто

.

За такими припущеннями Т-задача завжди має розв'язок за умови, що загальний обсяг продукції у постачальників не менший від загальної потреби споживачів (теорема про розв’язаність транспортної задачі):

Транспортна задача називається закритою коли виконується балансова умова і, у відповідності з вище вказаною теоремою, завжди має розв’язок. В інших відпадках транспортну задачу називають відкритою, при цьому можливі такі два випадки.

1. Загальний запас продукції в постачальників перевищує загальні потреби з боку споживачів:

У даному випадку, якщо ввести до розгляду додаткового (n+1)-го фіктивного споживача з потребою

одиниць продук­ції, то відкрита транспортна задача перетвориться на закриту. При цьому питомі вартості перевезень за фіктивними маршрутами вважають такими, що дорівнюють нулю.

2. Загальний запас продукції в постачальників менший від загальних потреб з боку споживачів:

У таких випадках може виникати інша задача: як оптимальним чином перевезти наявну продукцію (можливо і недостатню для задоволення потреб). Така нова задача може бути розв’язана введенням фіктивного (m+1) постачальника із запасом продукції a_m+1. При цьому, питомі вартості перевезень за фіктивними маршрутами вважаються рівними нулю, а обсяги перевезень x_m+1,j за цими маршрутами розглядаються для відповідних споживачів як недопостачання продукції через її дефіцит.

Умови транспортної задачі зазвичай записуються у табличному вигляді, як це показано у табл. 3.1.

Таблиця 3.1

Пункти відправлення (ПВ)	Пункти доставки (ПД)					Запаси аі
	B1	…	Bk	…	Bn
A1	c11 x11	…	c1k x1k	…	C1n x1n	a1
…	…	…	…	…	…	…
Al	cl1 xl1	…	clk xlk	…	cln xln	aL
…	…	…	…	…	…	…
Am	cm1 xm1	…	cmk xmk	…	cmn xmn	am
Потреби bj	B1	…	bk	…	bn	a