11.2. Характеристичні функції ігор з малим числом гравців

Як було сказано раніше, для кожної множини гравців N існує єдиний клас стратегічно еквівалентних несуттєвих ігор з множиною гравців N. Таким чином, залишається розглянути класи істотних кооперативних ігор.

Розглянемо спочатку класи ігри у (0,1)-редуційній формі для випадку ігор з нульовою сумою.

1. Ігри 2-х гравців. Будь-яка кооперативна гра двох гравців з нульовою сумою є несуттєвою.

Доведення. Припустимо, що мається істотна кооперативна гра двох гравців з характеристичною функцією , Тоді вона повинна бути стратегічно еквівалентна деякій грі в (0,1)-редуційній формі з характеристичною функцією ¹, що означає таке:

¹(1) = 0, ¹(2) = 0, ¹(1,2) = 1 (11.6)

З властивості додатковості повинно бути ¹(2) = ¹(1,2) – ¹(1) = 1 – 0 =1, що суперечить (11.6). А це значить, що припущення про істотність кооперативної гри двох гравців з нульовою сумою невірно.

Отже, клас кооперативних ігор двох гравців з нульовою сумою обмежується несуттєвими іграми.

2. Ігри 3-х гравців. Нехай  – характеристична функція істотної гри в (0,1)-редуційній формі, тоді

(1) = (2) = (3) = 0, (1,2,3) = 1.

З властивості додатковості маємо :

(1,2) = (1,2,3) – (3) = 1– 0 =1,

(1,3) = (1,2,3) – (2) = 1– 0 =1,

(2,3) = (1,2,3) – (1) = 1– 0 =1,

і, таким чином, характеристична функція цілком визначена. Отже, є два класи кооперативних ігор трьох гравців з нульовою сумою: клас істотних і клас несуттєвих ігор.

3. Ігри 4-х гравців. Розглянемо всі класи стратегічної еквівалентності таких ігор.

Насамперед є клас несуттєвих ігор у (0,1)-редуційній формі. Визначимо характеристичну функцію  такої гри:

(1) = (2) = (3) = (4) = 0, (1,2,3,4) = 1.

Виходячи з властивості додатковості, отримуємо

(1,2,3) = (1,2,3,4) – (4) = 1– 0 =1;

(1,2,4) = (1,2,3,4) – (3) = 1– 0 =1;

(1,3,4) = (1,2,3,4) – (2) = 1– 0 =1;

(2,3,4) = (1,2,3,4) – (1) = 1– 0 =1.

Тепер необхідно визначити значення характеристичної функції на коаліціях двох гравців. Усього таких коаліцій шість:

(1,2), (1,3), (1,4), (2,3), (2,4), (3,4).

Характеристична функція на цих коаліціях відповідно властивості додатковості задовольняє тільки наступним співвідношенням:

(1,4) = 1– (2,3),

(1,3) = 1– (2,4),

(1,2) = 1– (3,4).

Оскільки значень невідомих шість, а співвідношень тільки три, то їх значення із шести можуть бути обрані довільно. Позначимо ці довільні значення через x₁, x₂, x₃, тобто

(1,4) = x₁ , (2,4) = x₂ , (3,4) = x₃ .

Тоді

(2,3) = 1– x₁ , (1,3) = 1– x₂ , (1,2) = 1– x₃ .

Крім того повинно бути 0  x₁, x₂, x₃  1 , оскільки значення характеристичної функції на коаліції з двох гравців не може бути менше, ніж значення характеристичної функції для одного з цих гравців (рівне нулю для одного гравця), і не може бути більше, ніж значення характеристичної функції для коаліції з трьох гравців (рівне одиниці для трьох гравців). Геометрично (x₁, x₂, x₃) можна зобразити як точку одиничного куба, тобто кожному класу стратегічної еквівалентності ігор чотирьох гравців буде відповідати точка одиничного куба. Отже, множина класів стратегічної еквівалентності істотних ігор чотирьох гравців нескінченно і залежить від трьох довільних параметрів.

4. Ігри, що складаються з більше ніж 4 гравці, мають більшу розмаїтість класів стратегічної еквівалентності істотних ігор. Так, розмірність множини класів ігор n гравців дорівнює , тобто єдовільних параметрів.

Розглянемо тепер кооперативні ігри без умови постійності суми.

Для ігор 2-х гравців (множина N ={1,2}), умови редуційності дають

((() = ((1) = ((2) = ((1,2) = 1.

Таким чином, істотні кооперативні ігри двох гравців з ненульовою сумою складають один клас стратегічної еквівалентності.

Для ігор 3-х гравців (множина N ={1,2,3}), умови редуційності дають

() = (1) = (2) = (3) = 0; (1,2,3) = 1.

Значення характеристичної функції на множинах коаліцій двох гравців довільні (тут немає умови додатковості)

(1,2) = C₃, (1,3) = C₂, (2,3) = C₁,

але задовольняють умові

0  C₁, C₂, C₃  1.

Таким чином, класи стратегічної еквівалентності загальних кооперативних ігор трьох гравців можуть бути поставлені у відповідність точкам тривимірного одиничного куба.

Для ігор більш 3-х гравців з ненульовою сумою розгляд аналогічний.

Для дослідження ігор велике значення має можливість врахування переваги розподілу, що здійснюється за допомогою поняття домінування.

Означення11.2. Нехай є два розподіли x = (x₁, ..., x_n) і y = (y₁, ..., y_n) у кооперативній грі G = {N,}, і K N – деяка коаліція. Тоді розподіл x домінує y по коаліції K, якщо

1)  (K) (властивість ефективності домінуючого платежу);

2) x_i > y_i для всіх iK (властивість переваги).

Властивість ефективності означає, що порівнюваний коаліцією розподіл x повинен бути, реалізованим цією коаліцією: сума виграшів кожного з членів коаліції не повинна перевищувати впевнено отримувану нею кількість. Інакше коаліція, зустрівшись із розподілом, що дає їй стільки, скільки вона самостійно не в змозі дістати, повинна погодитися на нього і не займатися його порівнянням з будь-якими або іншими розподілами.

Умова переваги відображає необхідність “єдності” у перевазі з боку коаліції: якщо хоча б одна з нерівностей x_i > y_i буде порушена, тобто якщо хоча б для одного з членів коаліції K виграш в умовах розподілу y буде не меншим, ніж в умовах розподілу x, то можна буде говорити про перевагу розподілу x щодо розподілу y не всією коаліцією K, а тільки тими її членами, для яких відповідна нерівність x_i > y_i дотримується.

Співвідношення домінування x над y по коаліції K позначається через .

Означення 11.3. Розподіл x домінує y, якщо існує така коаліція K, для якої розподіл x домінує y. Це домінування позначається таким чином:

x > y.

Наявність домінування x > y означає, що на множині гравців N знайдеться коаліція, для якої x переважає y. Відношення домінування не характеризується цілком властивостями рефлексивності, симетрії, транзитивності, можливі тільки часткова симетрія і транзитивність. Співвідношення домінування можливе не по всякій коаліції. Так, неможливе домінування по коаліції, що складається з одного гравця або з усіх гравців.

Справедлива така теорема.

Теорема 11.3. Якщо  і ¹ – дві стратегічно еквівалентні характеристичні функції, причому розподілам x і y відповідають розподіли і, то зx > y випливає >.

Очевидно, що усі явища, що описуються в термінах домінування розподілів, відносяться до класів стратегічної еквівалентності, тому достатньо вивчати ці класи (а не самі ігри) для істотних ігор по їх (0,1)-редуційній формі, а для несуттєвих ігор - по нульових іграх. У будь-якій несуттєвій грі є тільки один розподіл, тому ніяких домінувань у ній немає.

Розглянемо домінування розподілів в істотній грі на такому прикладі.

Приклад 11.1. Нехай є (0,1)-редуційна форма істотної гри трьох гравців з постійною сумою (рівної 1). Оскільки домінування неможливе ні по одній з одноелементних коаліцій 1, 2, 3, а також по коаліції, що складається з усіх трьох гравців, то домінування можливе тільки по одній із двохелементних коаліцій {1,2}, {1,3}, {2,3}.

Для наочності домінування розподілів введемо поняття бароцентричних координат. Осями координат служать три осі x₁, x₂, x₃, що складають між собою однакові кути 60^о, вісь x₃ знаходиться на відстані одиниці від точки перетинання осей x₁ і x₂ (рис. 11.1), координати точки x = (x₁, x₂, x₃) – відповідно відстані від цієї точки до осей x₁, x₂, x₃, узяті з такими знаками, як зазначено на рис 11.1. (Наприклад, для точки x на рис. 11.1 x₁ < 0, x₂ > 0, x₃ > 0).

У

Рис.11.1

Рис.11.22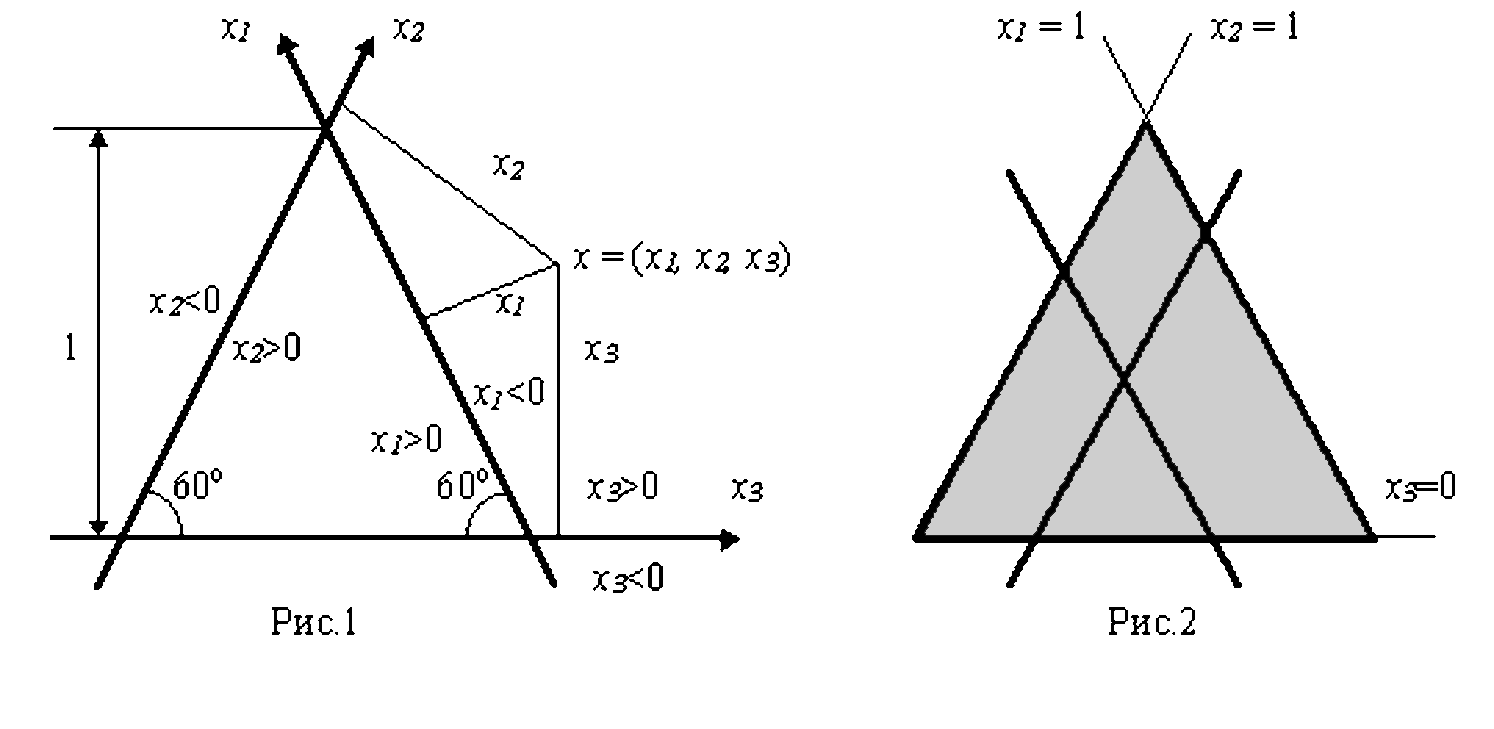

барицентрической системі координат завжди виконується рівність

x₁ + x₂ + x₃ = 1. (11.6)

На площині завжди є точка з координатами x₁, x₂, x₃, що задовольняють рівності (11.6). По цьому бароцентрична система координат автоматично задовольняє одній з умов, що визначають результат гри трьох гравців. З іншого боку, оскільки гра в (0, 1)-редуційній формі, то точка x повинна знаходитися в заштрихованому трикутнику (див. рис. 11.2). Розподіли x₁, x₂, x₃ повинні задовольняти нерівностям

x₁ + x₂  (1, 2), x₁ + x₃  (1, 3), x₂ + x₃  (2, 3).

З умови додатковості очевидно, що

x₁ + x₂ = 1  x₃  1 = (1, 2), x₁ + x₃  1, x₂ + x₃  1.

Розподіл x = (x₁, x₂, x₃) домінує розподіл y = (y₁, y₂, y₃)

по коаліції {1, 2}, якщо x₁ > y₁, x₂ > y₂;

по коаліції {1, 3}, якщо x₁ > y₁, x₃ > y₃;

по коаліції {2, 3}, якщо x₂ > y₂, x₃ > y₃,

тобто якщо розподіл y знаходиться в одному із показаних на рис. 11.3 паралелограмів, за винятком трьох граничних прямих, що проходять через точку x, то розподіл x домінує розподіл y, а будь-яка точка, що знаходиться в не заштрихованих трикутниках переважає x.

Таким чином, якщо x і y  два результати і жоден з них не переважає інший, то відповідні точки лежать на прямій, паралельній однієї з координатних осей.

x₃ =  1 x₂ =  1

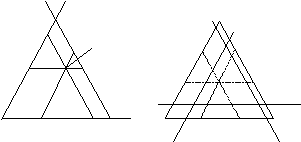x = (x₁, x₂, x₃)

x₃ = 1  C₃

x₁ = 0

x₁ = 1  C₁ x₂ = 1  C₂

Рис. 11.3 Рис. 11.4

Приклад 11.2. Нехай є (0, 1)-редуційна гра трьох гравців з ненульовою сумою.

Розглянемо спочатку умови домінування розподілу x = (x₁, x₂, x₃) над розподілом y = (y₁, y₂, y₃) по коаліції {1, 2}. У цьому випадку маємо :

(11.7)

Оскільки може бути так, що C₃ < 1 , то першу з умов (11.7) не можна відкинути, як це робиться в іграх з постійною сумою. Це значить що, x повинно бути не нижче прямої

x₁ + x₂ = C₃.

Або, з урахуванням (11.6), наведене вище рівняння прийме вигляд

x₃ = 1 + C₃ .

Таким чином, якщо розподіл x такий, що

x₁  1  C₁, x₂  1  C₂, x₃  1  C₃, (11.8)

то є три паралелограми, заштрихованих на рис. 11.4, знаходячись у яких, точки x домінують y.

Якщо в (11.8) одна з нерівностей, наприклад, третя не має місця, тобто тільки 2 паралелограми, заштрихованих на рис. 11.5, знаходячись у деяких точках x домінує y.

З розглянутого прикладу видно, що можливо багато варіантів, що виникають під час вивчення питань, зв'язаних з домінуванням розподілів у кооперативних іграх. З ростом числа гравців надзвичайно швидко росте кількість таких варіантів. У зв'язку з цим виникає необхідність виділення цілком стійких розподілів, тобто таких розподілів, що не домінуються ніякими іншими розподілами. Множина цілком стійких розподілів у коопе­ра­тивній грі називається с-ядром цієї гри.

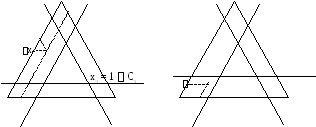x₁ = 1  C₁ x₂ = 1  C x₂ = 1  C₂ x₁ = 1  C₁

x₃ = 1  C₃

x

Рис. 11.5 Рис. 11.6

Теорема 11.4. Для того щоб розподіл x належав з-ядру кооперативної гри з характеристичною функцією , необхідно і досить, щоб для будь-якої коаліції K виконувалася нерівність

(11.9)

Оскільки нерівності (11.9) лінійні щодо x, то з останньої теореми випливає, що с-ядро в будь-якій кооперативній грі є опуклим багатокутником. До особливостей кооперативних ігор щодо існування с-ядра відносяться:

- у несуттєвій грі с-ядро існує і складається з єдиного розподілу цієї гри;

- у будь-якій істотній грі з постійною сумою с-ядро порожнє.

Для загальної гри трьох гравців у (0; 1)-редуційній формі маємо наступне (рис. 11.7).

Її характеристична функція має вигляд :

() = (1) = (2) = (3) = 0, (1, 2, 3) = 1,

(1, 2) = З₃; (1, 3) = З₂; (2, 3) = З₁,

де 0  З₁, З₂, З₃  1.

На підставі останньої теореми для належності розподілу x с-ядра необхідно і достатньо виконання нерівностей

x₁ + x₂  C₃, x₁ + x₃  C₂, x₂ + x₃  C₁,

або, використовуючи рівність x₁ + x₂ + x₃ = 1, одержимо

x₃  1  C₃, x₂  1  C₂, x₃  1  C₁. (11.10)

3

1 2

Рис. 11.7

Це означає, що точка x повинна лежати ближче до i-ої вершини основного трикутника (див. рис. 11.7), ніж пряма

_i = 1  С_i, (i = 1,2,3). (11.11)

З нерівності (11.10) шляхом підсумовування одержимо

x₁ + x₂ + x₃  3  (С₁ + С₂ + С₃)

або, з огляду на те, що x₁ + x₂ + x₃ = 1, одержимо

С₁ + С₂ + С₃  2. (11.12)

Нерівність (11.12) є необхідною умовою існування непорожнього с-ядра. З іншого боку, якщо (11.12) виконується, то можна взяти такі невід’ємні ₁, ₂, ₃, щоб

,

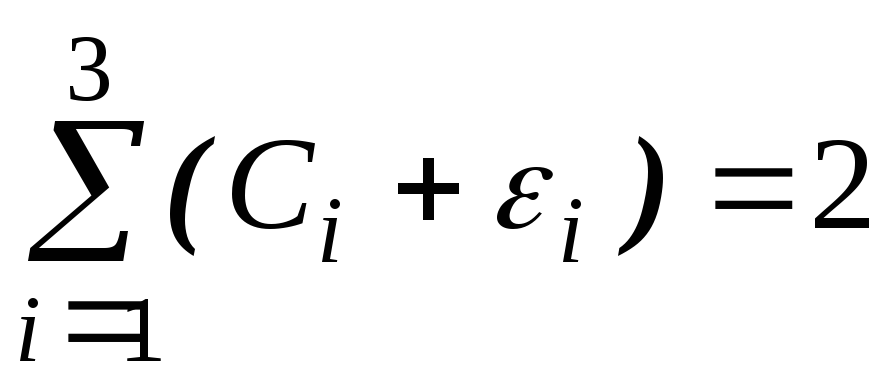і покласти

x_i = 1  C_i  _i (i = )

Такі значення x_i і задовольняють нерівностям (11.10), тобто такий розподіл x = (x₁, x₂, x₃) належить с-ядру.

Геометрично непорожнє с-ядро є заштрихованим трикутником (рис. 11.7), зі сторонами, що описуються рівняннями (11.11) за умови, що виконується співвідношення

₁ + ₂ + ₃ = 1,

і розв’зок будь-якої пари рівнянь (11) є невід’ємними. Так, наприклад, розглянемо систему

₁ = 1  С₁, ₂ = 1  З₂.

Оскільки 0  С₁  1, 0  С₂  1, то ₁, ₂  0. Звідси одержуємо

₃ = 1  ₁  ₂ = 1  (1  С₁)  (1  С₂) = С₁ + С₂  1.

Для того, щоб ₃  0, необхідно щоб С₁ + С₂  1  0 або С₁ + С₂  1.

3 3

1 2 1 2

Рис. 11.8 Рис. 11.9

У цьому випадку с-ядро, що наведено на рис. 11.7 усередині основного трикутника. Аналогічно розглядаються інші можливі варіанти сполучення нерівностей. Наприклад, якщо С₁+ С₂ < 1, то с-ядро має вигляд заштрихованого чотирикутника усередині основного трикутника (рис.11.8). Взагалі багатокутник, що представляє с‑ ядро, утвориться як опуклий багатокутник перетинанням прямих (11.11) і рядків основного трикутника. Якщо, наприклад, виконуються нерівності

С₁ + С₂ < 1; С₂ + С₃ < 1; С₁ + С₃ < 1,

то с-ядро буде у вигляді шестигранника (рис. 11.9).

Очевидно, у розв’язання кооперативної гри повинні входити розподіли, кращі з визначеної точки зору. Так, розподіли, що входять у с-ядро, є стійкими в трохи пасивному змісті, тобто за цих обставинах немає основ відхилятися від такого розподілу. Однак, знайти розподіл такий, що не тільки не домінувався б будь-якими іншими розподілами, але сам домінував би будь-який інший розподіл, не вдається. Тому розв’язок шукають на шляху розширення класу розподілів . І це розширення полягає у тому, що розв’язком гри повинен бути не один розподіл, а деяка їх множина.

Дж. фон Нейман і О. Моргенштерн запропонували вимагати від мно­жи­ни розподілів, що приймається як розв’язок кооперативної гри такі дві властивості: внутрішню стійкість, що полягає у в тому, щоб розподіли з розв’язку не можна було протипоставити один одному, і зовнішню стійкість, що полягає в можливості кожному відхиленню від розв’язку протиставляти деякий розподіл, що належить розв’язку. Таким чином ми приходимо до такого о означення.

Означення 11.4. Розв’язком по Нейману-Моргенштерну (Н-М- розв’язком) кооперативної гри називається множина R розподілів у ньому, що характеризується такими властивостями :

• внутрішня стійкість: ніякі два розподіли з R не домінують один одного;

• зовнішня стійкість: який би не був розподіл S, що не належить R, знайдеться розподіл r, що належить R, і який би домінував S.

Змістовна інтерпретація Н-М- розв’язку полягає у тому, що будь-які дві норми поведінки, що відповідають Н-М- розв’язку, не можуть бути протипоставлені один одному; яке б ні було відхилення від допустимих поведінок, знайдеться така коаліція, що буде прагнути до відновлення норми.

Теорема 11.5. Якщо в кооперативній грі існує с-ядро C і Н-М- розв’язок R, то C R.

Властивості Н-М- розв’язків.

Н-М- розв’язок кооперативної гри не може складатися тільки з одного розподілу, оскільки в цьому випадку характеристична функція гри несуттєва.

Недоліки Н-М- розв’язків.

1. Відомі приклади кооперативних ігор, що не мають Н-м-розв’язків. Більш того, у даний час не відомо критеріїв, що дозволяють судити про наявність у кооперативних ігор Н-м-розв’язків. Тим самим закладений у Н-м-розв’язках принцип оптимальності не є універсально реалізованим, і область його реалізації поки залишається невизначеною.

2. Кооперативні ігри, якщо не мають Н-м-розв’язку, то, як правило, більш одного розподілу. Тому принцип оптимальності, що приводить до Н-м-розв’язку, є не повним: узагалі говорячи, він не в змозі вказати гравцям єдиної системи норм розподілу виграшу.

3. Розв’язок істотних кооперативних ігор складається більш, ніж з одного розподілу. Таким чином, навіть вибір будь-якого конкретного Н-м-розв’язку ще не визначає виграшу кожного з гравців.

11. Поняття Н-м-розв’язку відображає тільки в дуже малій степені риси справедливості.

Перераховані недоліки відображають положення справ у дійсності: більшість економічних і соціальних проблем допускає множину рішень, і ці рішення не завжди піддаються безпосередньому порівнянню за їх перевагами.

Перераховані недоліки Н-М- розв’язків коаліційних ігор сприяють пошукам нових підходів. Одним з таких підходів є підхід Шепли, суть якого в тому, що він будується на підставі аксіом справедливості розподілів.

Означення 11.5. Носієм гри з характеристичною функцією  називається така коаліція T, що

(S) = (S  T)

для будь-якої коаліції S.

Зміст носія T полягає у тому, що будь-який гравець, що не належить T, є нейтральним, він не може нічого внести в коаліцію і йому нічого не слід виділяти із загального виграшу.

Означення 11.6. Нехай  – характеристична функція кооперативної гри n гравців,  – будь-яка перестановка множини N гравців. Через  позначимо характеристичну функцію такої гри, що для коаліції S = {i₁, i₂, ..., i} буде

u ({( i₁), ( i₂), ..., ( i)}) = (S).

Змістовний сенс функції  полягає у тому, що якщо в грі з характеристичною функцією  поміняти місцями гравців щодо перестановки , то отримаємо гру з характеристичною функцією .

Аксіоми Шепли.

1^о. Аксіома ефективності. Якщо S – будь-який носій гри з характеристичною функцією , то

= (S).

Іншими словами, “справедливість вимагає”, щоб під час розподілу загального виграшу носія гри нічого не виділяти стороннім, що не належать носієві, так само як і нічого не стягувати з них.

2^о. Аксіома симетрії. Для будь-якої перестановки  і iN повинне виконуватися

() = _i (),

тобто гравці, що однаково входять у гру, повинні “по справедливості” отримувати однакові виграші.

3^о. Аксіома агрегації. Якщо є дві гри з характеристичними функціями  і , то

 _i ( + ) =  _i () +  _i (),

тобто заради “справедливості” необхідно вважати, що при участі гравців у двох іграх їх виграші в окремих іграх повинні складатися.

Означення11.7. Вектором цін (вектором Шепли) гри з характеристичною функцією  називається n-мірний вектор

 () = (₁(), ₂(), ..., _n()),

що задовольняє аксіомам Шепли.

Існування вектора Шепли випливає з наступної теореми

Теорема 11.7. Існує єдина функція , що визначена для всіх ігор і задовольняє аксіоми Шепли.

Означення11.8. Характеристична функція _S(T), що визначена для будь-якої коаліції S, називається найпростішої, якщо

_S(T) =

Змістовно найпростіша характеристична функція описує таке положення справ, при якому множина гравців S виграє одиницю тоді і тільки тоді, коли воно містить деяку основну мінімальну коаліцію S, що виграє.

Можна довести, що компоненти вектора Шепли в явному вигляді запишуться як

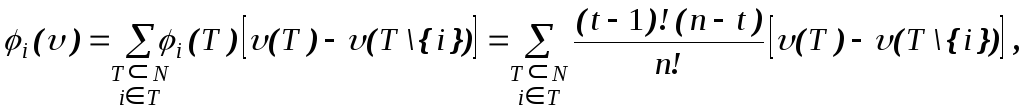
де t – число елементів у T.

Вектор Шепли змістовно можна інтерпретувати таким чином: гранична величина, що вносить i-й гравець у коаліцію T, описується як

(T)  (T \{i}),

і вважається виграшем i-го гравця; _i (T) – це ймовірність того, що i-й гравець вступить у коаліцію T \{i}; _i () – середній виграш i-го гравця в такій схемі інтерпретації. У тому випадку, коли  – найпростіша,

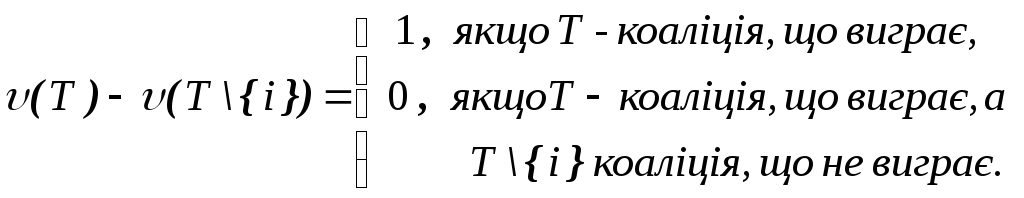
Отже

,

де підсумовування по T поширюється на всі такі коаліції, що виграють, і що коаліція T \{i} не є коаліцією, що виграє.

Приклад 11.3. Розглянемо корпорацію з чотирьох акціонерів, що мають акції відповідно в таких обсягах:

a₁ = 10; a₂ = 20; a₃ = 30; a₄ = 40.

Будь-яке рішення затверджується акціонерами, що мають у сумі більшість акцій. Це рішення вважається виграшем, що дорівнює 1. Тому дана ситуація може розглядатися як проста гра чотирьох гравців, де коаліціями, що виграють, є такі:

{2; 4}, {3; 4},

{1; 2; 3}, {1; 2; 4}, {2; 3; 4}, {1; 3; 4},

{1; 2; 3; 4}.

Знайдемо вектор Шепли для цієї гри.

Під час пошуку ₁ необхідно враховувати, що є тільки одна коаліція T = {1; 2; 3}, що виграє, а коаліція T \{1} = {2; 3} не виграє. У коаліції T є t=3 гравця, тому

.

Далі, визначаємо всі коаліції, що виграють, але не виграють без 2-го гравця: {2; 4}, {1; 2; 3}, {2; 3; 4}. Тому

.

Аналогічно отримуємо значення:

і .

У результаті вектор Шепли визначиться як

.

При цьому, якщо вважати, що вага голосу акціонера пропорційна кількості наявних у нього акцій, то отримаємо вектор голосування

,

який відрізняється від вектора Шепли.

Аналіз гри показує, що компоненти 2-го і 3-го гравців рівні, хоча третій гравець має більше акцій. Це виходить внаслідок того, що можливості утворення коаліцій у 2-го і 3-го гравця однакові. Для 1-го і 4-го гравця ситуація природна, що відповідає силі їх капіталу.