
- •Теория телетрафика
- •8.1. Общие сведения 88
- •9.1. Общие сведения 105
- •11.1. Общие сведения 140
- •1.1. Теория телетрафика – одна из ветвей теории массового обслуживания
- •1.2. Математические модели систем распределения информации
- •1.3. Основные задачи теории телетрафика
- •1.4. Общие сведения о методах решения задач теории телетрафика
- •1.5. Краткий исторический обзор развития теории телетрафика
- •Контрольные вопросы
- •2.1. Основные понятия
- •2.2. Принципы классификации потоков вызовов
- •2.3. Характеристики потоков вызовов
- •2.4. Простейший поток вызовов
- •2.5. Нестационарный и неординарный пуассоновские потоки
- •2.6. Потоки с простым последействием
- •2.7. Симметричный и примитивный потоки
- •2.8. Поток с повторными вызовами
- •2.9. Поток с ограниченным последействием. Поток Пальма
- •2.10. Просеивание потоков. Потоки Эрланга
- •2.11. Длительность обслуживания
- •2.12. Поток освобождений
- •Контрольные вопросы
- •3.1. Поступающая, обслуженная, потерянная нагрузки
- •3.2. Концентрация нагрузки
- •3.3. Основные параметры и расчет интенсивности нагрузки
- •3.4. Характеристики качества обслуживания потоков вызовов
- •3.5. Пропускная способность коммутационных систем
- •Контрольные вопросы
- •4.1. Обслуживание вызовов симметричного потока с простым последействием
- •4.2. Обслуживание вызовов простейшего потока
- •4.3. Обслуживание вызовов примитивного потока
- •Контрольные вопросы
- •5.1. Обслуживание вызовов простейшего потока при показательном законе распределения длительности занятия
- •5.2. Обслуживание вызовов простейшего потока при постоянной длительности занятия
- •5.3. Область применения систем с ожиданием
- •Контрольные вопросы
- •6.1. Постановка задачи
- •6.2. Предельная величина интенсивности поступающей нагрузки
- •6.3. Уравнения вероятностей состояний системы с повторными вызовами
- •6.4. Основные характеристики качества работы системы с повторными вызовами
- •Контрольные вопросы
- •7.1. Общие сведения
- •7.2. Моделирование случайных величин
- •7.3. Моделирование коммутационных систем на универсальных вычислительных машинах
- •7.4. Точность и достоверность результатов моделирования
- •Контрольные вопросы
- •8.1. Общие сведения
- •8.2. Некоторые характеристики неполнодоступных схем
- •8.3. Выбор структуры ступенчатой неполнодоступной схемы
- •8.4. Выбор структуры равномерной неполнодоступной схемы
- •8.5. Построение цилиндров
- •8.6. Идеально симметричная неполнодоступная схема
- •8.7. Формула Эрланга для идеально симметричной неполнодоступной схемы
- •8.8. Априорные методы определения потерь в неполнодоступных схемах
- •8.9. Инженерный расчет неполнодоступных схем
- •Контрольные вопросы
- •9.1. Общие сведения
- •9.2. Комбинаторный метод. Полнодоступное включение выходов
- •9.3. Потери в двухзвеньевых схемах при отсутствии сжатия и расширения
- •9.4. Потери в двухзвеньевых схемах при наличии сжатия или расширения
- •9.5. Двухзвеньевые неполнодоступные схемы
- •9.6. Метод эффективной доступности
- •9.7. Структура многозвеньевых коммутационных схем
- •9.8. Способы межзвеньевых соединений и методы искания в многозвеньевых схемах
- •9.9. Расчет многозвеньевых коммутационных схем в режиме группового искания. Метод клигс
- •9.10. Метод вероятностных графов
- •9.11. Оптимизация многозвеньевых коммутационных схем
- •Контрольные вопросы
- •10.1. Качество обслуживания на автоматически коммутируемых сетях связи
- •10.2. Расчет нагрузок на входах и выходах ступеней искания коммутационных узлов
- •10.3. Расчет нагрузок, поступающих на регистры и маркеры
- •10.4. Способы распределения нагрузки
- •10.5. Колебания нагрузки. Расчетная интенсивность нагрузки
- •Контрольные вопросы
- •11.1. Общие сведения
- •11.2. Обходные направления и использование метода эквивалентных замен при расчете числа линий в обходных пучках
- •11.3. Динамическое управление. Характер задач, возникающих при управлении потоками
- •11.4. Кроссовая коммутация как управление структурой сети
- •11.5. Метод укрупнения состояний пучков при определении характеристик управляющей информации
- •Контрольные вопросы
- •12.1. Цели и задачи измерений
- •12.2. Принципы измерений параметров нагрузки и потерь
- •12.3. Обработка результатов измерений
- •12.4. Определение объема измерений
- •Контрольные вопросы
- •Список литературы
Контрольные вопросы
1. Укажите основные особенности ступенчатой и равномерной неполнодоступных схем и их отличие.
2. Какими параметрами характеризуется структура ступенчатой НС?
3. Какими параметрами характеризуется структура равномерной НС?
4. Составьте матрицы связности для четвертого, шестого и девятого вариантов структуры шестигрупповой НС, приведенной на рис. 8.2, и сравните их.
5. Определите структурные параметры двухгрупповой (g=2) ступенчатой НС на 14 выходов (=14) при доступности d=10.
6. Определите число возможных вариантов структуры неполнодоступной НС при d=10, =30, g=6.
7. Определите структурные параметры четырехгрупповой равномерной НС при d= 10 и =16.
8. Определите число нагрузочных групп идеально симметричной НС для случайного равновероятного искания при =16 и d=10.
9. Определите вероятность потерь в идеально симметричной НС с параметрами =3, d=2 при интенсивности поступающей нагрузки у=1 Эрл.
10. Укажите, как зависит число выходов НС от доступности при заданных нагрузке и вероятности потерь.
11. Укажите, как зависит число выходов НС от качества обслуживания (вероятности потерь) при заданных нагрузке и доступности.
12. Изобразите характер зависимости среднего использования выхода НС от общего числа выходов при заданных доступности я вероятности потерь.
ГЛАВА ДЕВЯТАЯ
Звеньевые коммутационные системы
9.1. Общие сведения
Особенности звеньевых коммутационных схем заключаются в том, что в соединении между одним из входов и одним из выходов схемы кроме точек коммутации участвуют также промежуточные линии (ПЛ).
Р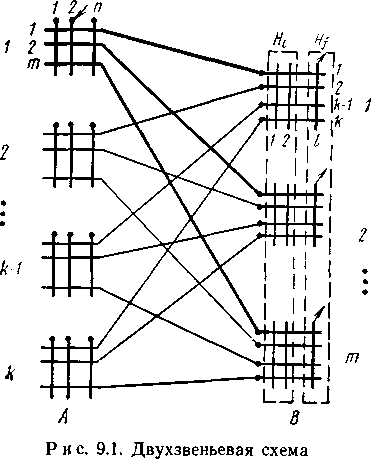 ассмотрим
двухзвеньевую схему, приведенную на
рис. 9.1, у которой любой выход схемы
доступен любому входу (полнодоступный
пучок выходов). Схема изображена в общем
виде и имеет k коммутаторов в первом
звене на п входов и т выходов
каждый и т коммутаторов во втором
звене на k входов и l выходов
каждый. Выходы схемы разбиты на группы
(направления). На рисунке показано два
направления – направление Hi,
к которому отнесены по два выхода в
каждом коммутаторе второго звена и
имеющее таким образом 2т выходов, и
направление Hj, имеющее т
выходов (по одному выходу в каждом
коммутаторе второго звена). В общем
случае число выходов в каждом коммутаторе,
отводимых для одного направления, может
быть равно q, и тогда суммарное число
выходов в направлении составит тq.
ассмотрим
двухзвеньевую схему, приведенную на
рис. 9.1, у которой любой выход схемы
доступен любому входу (полнодоступный
пучок выходов). Схема изображена в общем
виде и имеет k коммутаторов в первом
звене на п входов и т выходов
каждый и т коммутаторов во втором
звене на k входов и l выходов
каждый. Выходы схемы разбиты на группы
(направления). На рисунке показано два
направления – направление Hi,
к которому отнесены по два выхода в
каждом коммутаторе второго звена и
имеющее таким образом 2т выходов, и
направление Hj, имеющее т
выходов (по одному выходу в каждом
коммутаторе второго звена). В общем
случае число выходов в каждом коммутаторе,
отводимых для одного направления, может
быть равно q, и тогда суммарное число
выходов в направлении составит тq.
В простейших однозвеньевых коммутационных схемах с полнодоступным включением выходов, которые называют коммутаторами, обслуживание поступающего на вход вызова заключается вподключении к этому входу свободного выхода в одной точке коммутации (одно звено соединения). В более сложных неполнодоступных схемах (см. рис. 8.1) при установлении соединения устанавливается путь, содержащий также только одно звено.
В двухзвеньевой коммутационной схеме для установления соединения входа с выходом требуются две точки коммутации и одна из промежуточных линий, и, таким образом, соединительный путь содержит два звена соединения – ПЛ и выход.
Коммутационные схемы, содержащие два и более звеньев в соединительном пути, называют звеньевыми. В общем случае звеньевая схема – это схема, имеющая входы, выходы, коммутаторы и промежуточные линии. Все эти элементы взаимно связаны между собой и образуют некоторую структуру, которая позволяет соединить вход с выходом, используя определенные промежуточные линии и точки коммутации, т. е. устанавливая соединительный путь между входом и выходом. Каждый соединительный путь в схеме можно задать упорядоченным набором промежуточных линий. При этом любые две соседние промежуточные линии соединительного пути могут быть соединены между собой в точке коммутации. Если все промежуточные линии и выход, составляющие соединительный путь, свободны, то и этот путь свободен. Соединительный путь считается занятым, если хотя бы одна из промежуточных линий или выход заняты.
Любая звеньевая схема имеет конечное число состояний, каждое из которых отличается комбинацией занятых входов, выходов и промежуточных линий.
По сравнению с однозвеньевыми полнодоступными схемами, рассмотренными в гл. 4–6, и однозвеньевыми неполнодоступными схемами, рассмотренными в гл. 8, звеньевые схемы имеют большее число состояний. Поэтому для звеньевых схем, представляющих практический интерес, система уравнений для вероятностей состояний во многих случаях не может быть решена, а в отдельных случаях не может быть даже выписана.
Исследование звеньевых схем сложно не только из-за их большого числа состояний. Дополнительные усложнения возникают также и из-за того, что между процессами, происходящими в разных направлениях выходов звеньевой схемы, существует взаимная зависимость. Это можно уяснить, рассматривая схему на рис. 9.1. Для установления соединения к выходам направлений Hi и Hj используются одни и те же промежуточные линии. Поэтому занятие промежуточных линий для подключения к выходам одного направления изменяет вероятность занятия выходов другого направления.
Если для звеньевой схемы предположить, что существуют условные вероятности блокировки i, которые зависят лишь от числа занятых выходов, то для простейшего потока вызовов и показательного распределения длительности занятия можно записать уравнения для вероятностей состояний и воспользоваться методом условных вероятностей, разработанным Г. П. Башариным. Однако в общем случае условные вероятности блокировки зависят не только от числа занятых выходов, но и от структуры схемы, поступающей нагрузки и алгоритма установления соединения, что усложняет задачи исследования звеньевой схемы. В связи с этим инженерный расчет звеньевых схем основывается на априорных предположениях относительно способа математического описания результатов воздействия поступающего потока вызовов на отдельные звенья соединения. Обычно предполагается, что процессы, протекающие в различных звеньях схемы, независимы и могут быть описаны каким-нибудь простым законом распределения; кроме того, используются и другие упрощающие предположения. Это облегчает решение задачи, однако вносит отклонение от истинных характеристик, имеющих место в процессе функционирования схемы.
В большинстве случаев нельзя заранее указать, в какой степени то или иное упрощающее предположение искажает истинную величину отыскиваемого показателя (например, вероятности потерь), поэтому для определения степени погрешности приближенных методов можно воспользоваться сравнением с результатами моделирования на ЭВМ. Поскольку наиболее простыми звеньевыми схемами являются схемы с двумя звеньями соединения, то в первую очередь изучим методы расчета потерь в таких схемах.
Из самых распространенных в настоящее время приближенных инженерных методов расчета двухзвеньевых схем рассмотрим два метода: комбинаторный метод Якобеуса и метод эффективной доступности. Сейчас существует тенденция разработки методов расчета числа соединительных устройств с использованием результатов статистического моделирования на ЭВМ. Полученные результаты, как правило, аппроксимируются какими-нибудь простыми функциональными зависимостями. Так как практически невозможно получить числовые данные для любых значений нагрузки и параметров структуры, которые могут встретиться при расчетах, то такого типа методы предполагают интерполяцию и экстраполяцию в области, где числовые данные не получены.
