Задача 6.5.

Задача планування виробничої лінії.

Оптимізувати режим функціонування виробничої лінії, яка охоплює 11 операцій з виготовлення двох виробів. Лінію обладнано одним багатоопераційним верстатом. Послідовність і тривалість (у хвилинах) виконання операцій відбиває рис. 6.3.

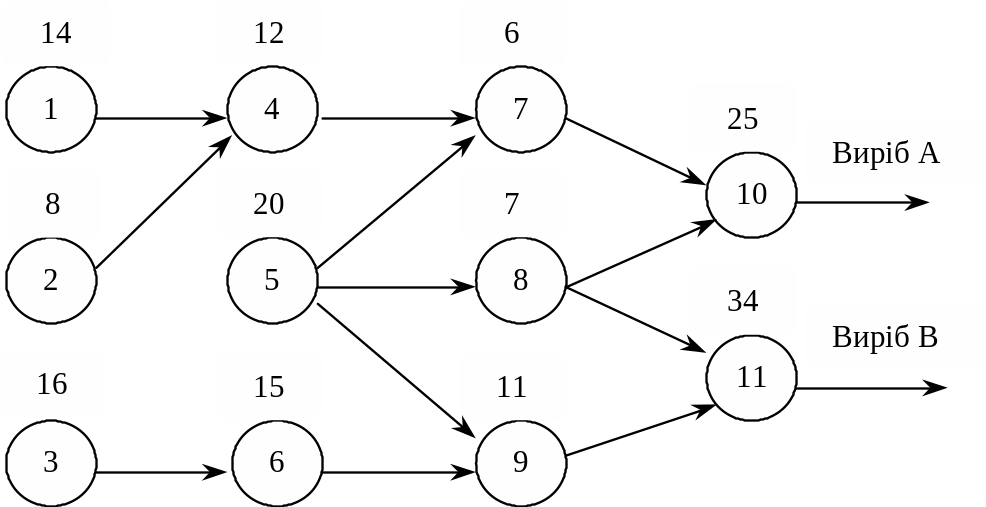
Рис. 6.3

Установлено термін виготовлення кожного з виробів А та В як проміжок часу від деякого початкового моменту. Нехай це буде відповідно 120 і 150 хв. Передбачається, що в кожний момент часу на верстаті може виконуватися одна операція.

Визначити оптимальний термін початку кожної операції.

Розв’язування. Розглянемо спочатку задачу в загальному вигляді, скориставшись позначеннями:

a_j(k) — час виконання j-ї операції ; d_j — момент часу (термін) для j-го виробу, до якого необхідно завершити операцію j; х_j — час (термін) початку j-ї операції; t — сумарний час виконання всіх операцій. Економіко-математична модель містить три типи обмежень.

1. Послідовність виконання i-ї операції записується для всіх пар операцій якщо i-та операція передує в часі j-й операції.

2. Обмеження нерозгалуженості виробничого процесу для операцій і та j, які не виконуються одночасно (i ≠ j), має вигляд:

або x_i – х_j ≥ a_j, якщо операція j передує в часі операції і; або x_j – х_i ≥ a_i, якщо операція і передує в часі операції j.

Зауважимо, що логічні обмеження виду «або-або» не можуть входити до економіко-математичної моделі задачі лінійного програмування, оскільки породжують неопуклу множину допустимих розв’язків. Тому необхідно ввести допоміжні змінні, які дозволяють записати наведені щойно логічні умови у вигляді лінійних обмежень. Це такі бульові змінні:

Увівши змінні y_ij, запишемо шукані обмеження:

,

,

де М — досить велике число.

3. Обмеження щодо термінів виготовлення кожного виробу:

,

де j — остання операція для k-го виробу.

4. Усі операції мають бути виконанні до моменту часу t:

.

Критерій оптимальності:

тобто ставиться задача, щоб обидва вироби були виготовлені за мінімальний час.

Запишемо числову економіко-математичну модель:

за наведених далі умов.

1. Послідовність виконання операцій:

,

,

,

,

,

,

,

,

,

,

,

.

2. Обмеження щодо нерозгалуженості виробничого процесу:

,

,

,

,

,

,

,

.

3. Обмеження щодо термінів виготовлення виробів:

,

.

4. Усі операції мають бути виконані до моменту часу t:

,

,

,

,

,

,

,

,

,

,

.

5. Обмеження на змінні:

, ;

, .

Отже, маємо частково цілочислову задачу з бульовими змінними.

Задача 6.6.

Задача оптимального призначення.

Розподілити чотирьох робітників за чотирма видами устаткування так, щоб їх загальна продуктивність праці була максимальною. Дані стосовно продуктивності праці кожного робітника на устаткуванні кожного виду наведено в таблиці:

Робітник	Продуктивність праці, грн./год, на устаткуванні
	1	2	3	4
1	12	9	8	7
2	10	7	6	5
3	9	6	4	4
4	8	5	3	2

Розв’язування. Дану задачу можна розглядати як транспортну, в якій робітники ототожнюються з постачальниками вантажів, а види устаткування — зі споживачами цих вантажів. Обсяги пропозиції та попиту в кожному випадку дорівнюють одиниці. Отже, змінні будуть бульовими:

Якщо c_ij — продуктивність праці і-го робітника на j-му устаткуванні, то економіко-математичну модель про призначення у загальному вигляді можна записати так:

за умов

,

,

,

.

Числова модель набирає вигляду:

за умов

,

,

,

,

,

,

,

,

,

— цілі числа .

З огляду на особливу структуру цієї задачі, зокрема її «транспортний» характер та рівність правих частин обмежень, для розв’язування можна застосувати ефективніший алгоритм, ніж для звичайної задачі цілочислового програмування з бульовими змінними. Пропонуємо читачеві ознайомитися з такими алгоритмами самостійно [9; 38].