Величина полного ускорения

(3.6)

Скорость и пройденный путь при прямолинейном равнопеременном движении определяются, соответственно, по формулам:

υ = υ₀ ± at (3.7)

(3.8)

(3.9)

(3.10)

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени (показывает на какой угол поворачивается радиус-вектор в единицу времени):

[рад/с] (3.11)

Вращение тела с постоянной по величине угловой скоростью называется равномерным. В этом случае угловая скорость может быть определена

(3.12)

Равномерное движение можно характеризовать периодом вращения Т (с) – промежутком времени, в течение которого вращающееся вокруг неподвижной оси тело совершает полный оборот, т.е. поворачивается на угол  = 2.

Тогда угловая скорость равна

(3.13)

(3.14)

Число полных оборотов, совершаемых телом при равномерном вращении в единицу времени называется частотой обращения:

v (3.15)

откуда

ω = 2πv (3.16)

угловое ускорение тела, равный первой производной его угловой скорости или второй производной от угла поворота по времени:

[рад/с².] (3.17)

Формулы связи угловых и линейных величин:

υ = r · ω (3.18)

a_τ = r · ε (3.19)

a_n = r · ω² (3.20)

S = r · φ (3.21)

В случае равнопеременного вращения ε = const.

ω = ω₀ + εt. (3.22)

. (3.23)

Примеры решения задач.

1 . Круглый конус с радиусом основания r и высотой h катится без скольжения по поверхности стола, как показано на рисунке 3.2. Вершина конуса закреплена шарнирно в точке О на уровне точ­ки С - центра основания конуса. Точка С движется с постоянной скоростью υ. Найти относительно стола: 1) угловую скорость ω ко­нуса; 2) его угловое ускорение ε.

Р ешение.

1. Согласно ω = ω₀ + ω′, где ω₀ и ω′ ­угловые скорости вращения вокруг осей 00' и ОС соответственно. Модули векторов ω₀ и ω′ легко найти с помощью рисунка:

.

Их отношение . Отсюда следует, что вектор ω совпадает в каждый момент с образующей конуса, которая проходит через точ­ку касания А.

Модуль вектора ω

.

2. Угловое ускорение ε конуса, есть производ­ная вектора по времени. Так как ω₀ = const, то

.

Вектор ω′, оставаясь постоянным по модулю, поворачивается вокруг оси 00' с угловой скоростью ω₀. Его приращение за промежуток времени dt равно по модулю |dω′| = ω′ω₀ dt, или в векторном виде dω′ = [ω′ω₀]dt. Таким образом,

ε = [ω′ω₀]

Модуль этого вектора .

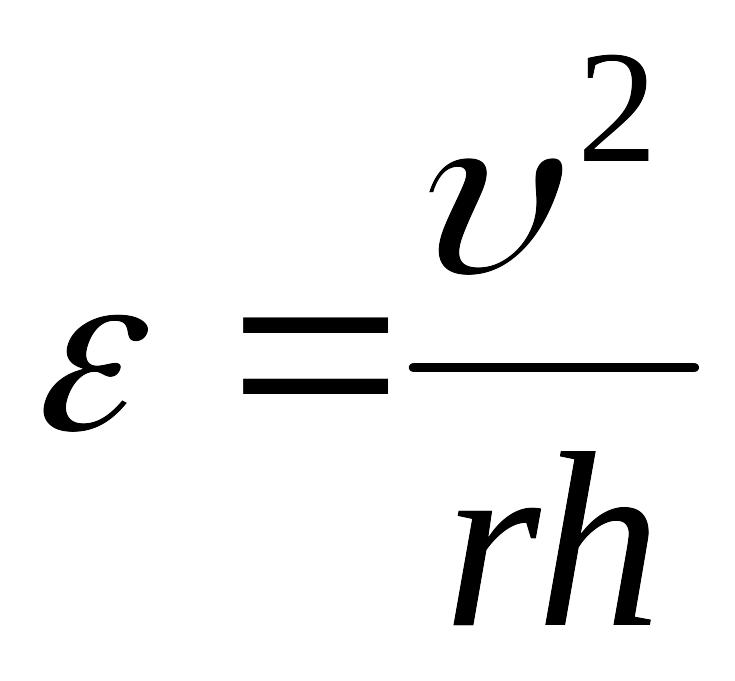Ответ: ; .

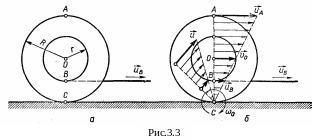
2. Катушка с намотанной на ней нитью лежит на горизонтальной поверхности стола (рис. 3.3 а) и может катиться по ней без скольжения. С какой скоростью будет перемещаться ось катушки, если конец нити тянуть в горизонтальном направлении со скоростью ? Радиус внутренней части катушки r, внешней - R. Каковы будут скорость и ускорение точки А?

Р ешение.

1-й способ. Качение катушки по столу можно представить как результат наложения двух одновременных независимых движений: переносного поступательного движения всех точек катушки с одинаковыми скоростями , равными по модулю скорости оси катушки и относительного – вращения вокруг её оси с некоторой угловой скоростью ω₀. Учитывая это, абсолютную (результирующую) скорость произвольной точки катушки (в том числе и В), удалённой от её оси на расстояние σ, можно представить как векторную сумму скоростей этой точки в переносном и относительном движении, т.е.

, (1)

где υ = ωσ - линейная скорость точки, обусловленная круговым относительным движением.

Угловая скорость ω₀ определяется из условия, что катушка катится по поверхности стола без скольжения. Точка С катушки в момент соприкосновения с поверхностью стола не движется относительно стола, её абсолютная скорость u_C = 0. Для этой точки σ = R и, следовательно, относительная скорость движения, направленная влево, равна по модулю переносной скорости, направленной вправо, т.е.

(2)

В задаче дана абсолютная скорость точки В, , равная по модулю скорости конца нити, и надо найти переносную скорость (абсолютную скорость оси катушки) и скорость точки А.

Согласно выражениям (1) и (2) с учётом направления относительных скоростей точек В и А и того, что σ_B = r и σ_A = R, получим для u и u_A соответственно:

,

откуда и .

Переносное движение всех точек катушки является равномерным поступательным, поэтому для всех точек a_n = 0 и их полное ускорение равно относительному ускорению: . Относительное ускорение представляет собой нормальное ускорение, вызванное равномерным вращением катушки вокруг её оси, поэтому

.

2-й способ. Движение катушки по столу есть плоскопараллельное движение твёрдого тела без проскальзывания, так как скорость точки С в данный момент времени равна нулю. Если принять ось, проходящую через точку С перпендикулярно плоскости чертежа, за мгновенную ось вращения, то качение катушки можно представить как непрерывный ряд мгновенных поворотов вокруг линии опоры с некоторой угловой скоростью ω₀ (рис.3.3 б). Связь между абсолютной скоростью u произвольной точки катушки, удалённой от мгновенной оси вращения на расстояние х, и ω₀ даётся формулой u = ω₀x.

Учитывая, что для точек В, О и А x_B = R – r, x_o = R, x_A = 2R и что абсолютная скорость точки В равна скорости конца нити ( u_B = u), получим для этих точек:

u = ω₀(R – r ); υ₀ = ω₀R; u_A = 2 ω₀R

Решая систему относительно искомых неизвестных, получим:

и .

Несмотря на то, что мы нашли скорость точки А, её ускорение нельзя сразу определить по формуле нормального ускорения, т.к. нам неизвестен радиус кривизны траектории точки. Следует обратить внимание, что если он равен не 2R, как это может показаться, а 4R (рекомендуется это доказать), поэтому для нахождения a_A нужно поступить точно также, как это было сделано в первом случае.

При отклонении нити от горизонтального положения вверх – увеличении угла между нитью и плоскостью стола – угловая скорость вращения катушки вокруг мгновенной оси будет уменьшаться (поскольку уменьшается расстояние х при неизменной скорости u). В том случае, когда нить составит с горизонтом угол α₀, при котором продолжение нити пройдёт через точку С ( радиус x = 0), катушка будет вращаться на месте. При углах α > α₀ катушка начнёт двигаться влево.

Ответ: ; ; .

3. Поезд тронулся с места и на некотором участке пути двигался равноускоренно с ускорением 0,2 м/с². Определить его скорость в конце второй минуты и путь, пройденный им за это время. Начертить графики координаты, пути и скорости.

Р ешение.

По условию вид движения равноускоренный с начальной скоростью равной нулю. Тогда скорость определим по формуле:

υ = υ₀ ± at = at = 0,2 · 120 = 24м/с,

а путь как произведение средней скорости на время движения:

м.

Графики для данного вида движения будут выглядеть как ниже изображено.

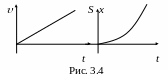
Ответ: υ = 24м/с; S = 1440м.

4. Колесо, вращаясь равнозамедленно, при торможении уменьшило свою частоту вращения за 1 мин с 300 об/мин до 180 об/мин. Найти угловое ускорение колеса и число оборотов, сделанных им за это время.

Р ешение.

Угловое ускорение найдём из уравнения скорости при равнозамедленном вращательном движении, выразив угловую скорость через частоту вращения:

.

После подстановки числовых значений, получаем:

рад/с ².

Для нахождения числа оборотов используем уравнение углового пути при равнозамедленном вращательном движении:

об.

Ответ: ε = 0,21рад/с ²; N = 240об.