Примеры решения задач.

1. Каково соотношение между высотой H горы и глубиной h шахты, если период колебаний математического маятника на вершине горы и на дне шахты один и тот же.

Р ешение.

Период колебаний математического маятника

Т.к. по условию периоды колебаний равны, то равны и ускорения свободного падения g_h = g_H.

Но

.

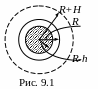
Тело, находящееся на глубине h под землёй, не испытывает со стороны вышележащего шарового слоя толщиной h никакого притяжения, т.к. притяжения отдельных частей слоя взаимно компенсируются. Масса заштрихованной части Земли:

Тогда

(1)

Отдельно преобразуем выражения, входящие в уравнение (1):

Поскольку , то . Аналогично

Тогда из (1)

(2)

На высоте имеем: , где ; r₂ = R + H, т.е.

(3)

Поскольку H << R, то

Тогда из (3) получаем:

(4)

Поскольку g_h = g_H, то, приравняв правые части (2) и (4), получим:

(5)

Воспользуемся выражением для суммы бесконечно убывающей геометрической прогрессии . При q << 1; . Тогда уравнение (5) можно записать в виде:

Слагаемым ввиду его малости можно пренебречь. Тогда

.

Ответ: h = 2H.

2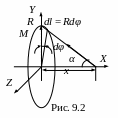 . Определить напряжённость поля тяготения тонкого кольца радиусом R и массы M в точке А (рис. 9.2), расположенной на оси кольца на расстоянии х от его плоскости.

Решение.

Ф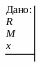 изическая система состоит из кольца и его поля тяготения. Необходимо решить основную задачу поля тяготения – рассчитать поле кольца. Но кольцо нельзя считать материальной точкой.

Разделим кольцо на столь малые элементы, чтобы каждый из них можно было считать материальной точкой. Рассмотрим один такой элемент dl = Rdφ (рис. 9.2). Он создаёт поле тяготения, вектор напряжённости которого в точке А равен , а его модуль

, (1)

где - масса элемента dl. Вектор составляет угол α с осью ОХ и угол φ с осью OZ. Проекция вектора на ось ОХ

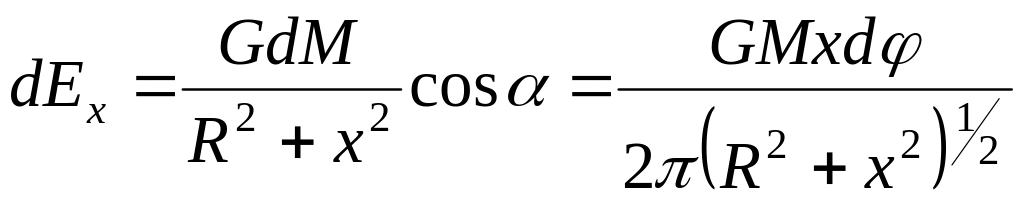(2)

После интегрирования (2) по углу φ находим проекцию искомого вектора напряжённости на ось ОХ:

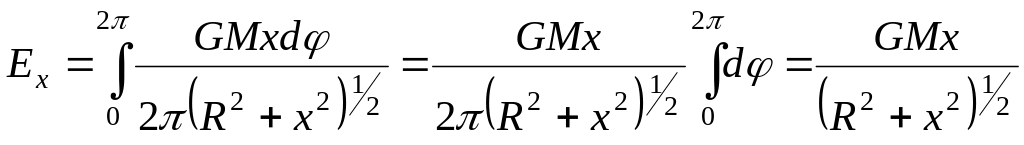(3)

Легко видеть, что в силу симметрии сумма проекций элементарных напряжённостей на оси OY и OZ равны нулю. Следовательно, искомый вектор напряжённости направлен вдоль оси ОХ и его модуль выражается формулой (3). После расчёта поля напряжённости кольца можно поставить ряд задач на движение тел в этом поле.

Ответ: .

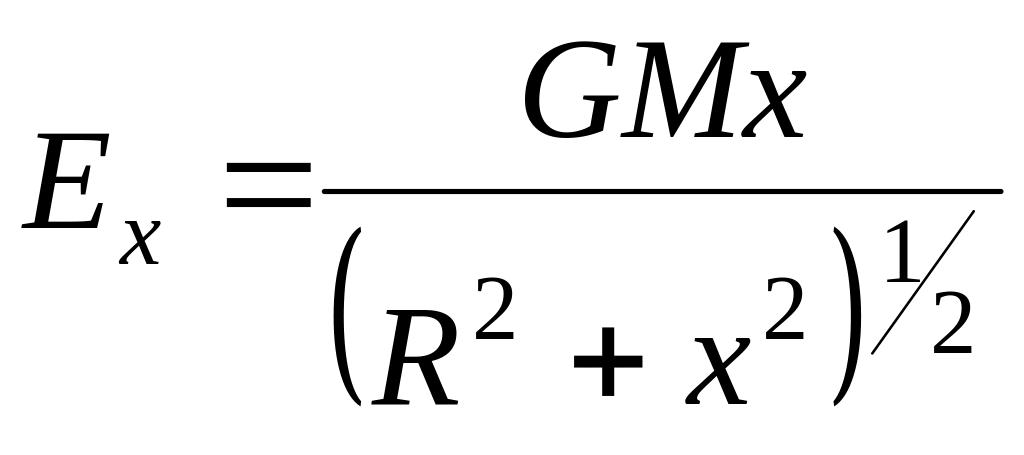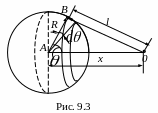
3. Сфера массы M и радиуса R разделена на две полусферы плоскостью, проходящей через её центр. Определить потенциал поля тяготения каждой полусферы в точке О, расположенной на прямой (перпендикулярно делящей плоскости и проходящей через центр сферы) на расстоянии x > R от центра сферы (рис. 9.3).

Р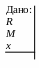 ешение.

Для расчёта поля тяготения каждой полусферы (не материальные точки) применим метод ДИ. Разделим каждую полусферу на узкие кольца ширины Rdθ и радиуса Rsinθ. Рассмотрим одно такое кольцо. Его площадь

dS = 2πRsinθ ∙ Rdθ = 2πR²sinθ ∙ dθ (1)

а масса

(2)

Так как все элементы этого кольца находятся на одинаковом расстоянии l от точки О, то элементарный потенциал поля тяготения этого кольца в точке О

(3)

Из треугольника АВО, по теореме косинусов

l² = R² + x² – 2Rxcos θ (4)

После дифференцирования последнего соотношения

Подставив это соотношение в (3), окончательно получим выражение для элементарного потенциала, как функции одного переменного l:

(5)

Можно было бы выразить элементарный потенциал, как функцию одного переменного угла θ (исключив l и (3) с помощью (4)). В этом случае интегрирование будет более сложным, чем интегрирование соотношения (5).

Обозначив U₁ потенциал правой полусферы, U₂ - потенциал левой, после интегрирования (5) находим

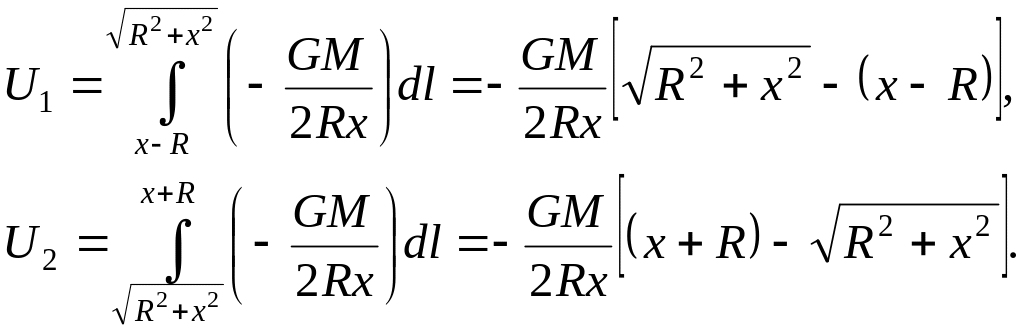
Сложив эти уравнения, получим выражение для потенциала поля тяготения сферы в точке, расположенной вне сферы

Тем же методом можно рассмотреть случай, когда x < R. Также можно рассчитать поле тяготения вне и внутри однородного шара.

Ответ: .

4. Какую скорость относительно поверхности Земли должен иметь искусственный спутник, чтобы лететь по круговой орбите, расположенной в плоскости экватора, на высоте h = 1600км над Землёй? Радиус Земли принять равным R = 6400км, ускорение свободного падения у её поверхности g = 9,8м/с².

Р ешение.

Если пренебречь силами притяжения, действующими на спутник со стороны небесных тел, и не учитывать сопротивление среды, можно с достаточной степенью точности считать, что на спутник при его движении действует только сила земного притяжения F.

Под действием этой силы спутник равномерно движется по окружности радиусом R + h с некоторой скоростью относительно Земли. Сила притяжения сообщает спутнику нормальное ускорение, равное по модулю и направленное к центру Земли.

Согласно второго закона Ньютона

(1)

Модуль силы тяготения в уравнении второго закона Ньютона нужно представить в развёрнутом виде, используя закон всемирного тяготения:

(2)

Если в решении задач подобного типа фигурирует масса Земли, расчёты можно значительно упростить, исключив произведение GM с помощью формулы

(3)

Скорость спутника относительно поверхности Земли равна:

u = υ ± υ₀, (4)

где υ₀ - линейная скорость точек Земли на экваторе, которую можно найти из соотношения

(5)

Знак «плюс» или «минус» в уравнении (4) берётся в зависимости от того, запущен ли спутник с востока на запад или с запада на восток.

Уравнения (1) – (5) содержат шесть неизвестных величин: F, M, m, υ, υ₀, u. Решая систему относительно скорости спутника, находим:

.

Подставляя числовые значения в выражение для скорости, находим:

u₁ ≈ 7,6км/с и u₂ ≈ 6,6км/с.

Эти результаты показывают, что запускать искусственные спутники Земли легче в направлении с запада на восток, чем в противоположном.

Ответ: u₁ ≈ 7,6км/с; u₂ ≈ 6,6км/с.

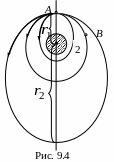
5. Два искусственных спутника Земли движутся по одной и той же круговой орбите на расстоянии L друг от друга, причём величина L много меньше радиуса орбиты. Период обращения спутника равен T. Как можно сблизить спутники на орбите, если на одном из них есть двигатель, с помощью которого можно практически мгновенно сообщить некоторую дополнительную скорость Δυ, малую по сравнению с орбитальной скоростью и направленную по касательной к траектории? Как скорость Δυ связана с L и T?

Р ешение.

На рисунке 9.4 показана круговая траектория радиусом r₁, по которой движутся спутники на расстоянии L друг от друга. Если в произвольной точке А спутнику сообщить дополнительную скорость Δυ в направлении орбитального движения, то он будет двигаться по эллиптической орбите 1 с фокусом в центре Земли. Период обращения по такой орбите больше, чем по круговой. Если же дополнительную скорость в точке А направить против движения по орбите, то спутник перейдёт на эллиптическую орбиту 2, период обращения по которой меньше T.

Отсюда становится ясным, какие манёвры следует производить для сближения спутников. Прежде всего отметим, что поскольку круговая и эллиптические орбиты имеют только одну общую точку А, встреча спутников может произойти только в этой точке. Поэтому встреча может произойти только через промежуток времени после совершения манёвра, кратный периоду обращения спутника по эллиптической орбите. Если двигатель установлен на спутнике, идущем впереди, то его нужно разогнать, переводя на орбиту 1. Если же двигатель находится на спутнике, идущем сзади, то его нужно тормозить, переводя на орбиту 2. Обратите внимание на кажущийся парадокс: для того, чтобы догнать, нужно притормозить!

Для определённости рассмотрим первый случай: в момент совершения манёвра пассивный спутник находится в точке В, отстоящей на L от точки А. Найдём величину дополнительной скорости Δυ, которую нужно сообщить активному спутнику, чтобы встреча произошла через один оборот. Обозначим через υ скорость движения по круговой орбите. Тогда период обращения T₁ по эллиптической орбите должен быть больше периода обращения T по круговой на время прохождения дуги L по круговой орбите:

(1)

Найдём связь между периодом обращения T₁ по эллиптической орбите и той добавочной скоростью Δυ, которая переводит спутник на эту орбиту. В этом нам помогут законы Кеплера. На основании третьего закона Кеплера

(2)

где - большая полуось эллипса (рис. 10.4).

Для того чтобы связать расстояние r₂ от центра Земли до апогея эллиптической орбиты с Δυ, воспользуемся вторым законом Кеплера и законом сохранения энергии: обозначив через υ₁ = υ + Δυ и υ₂ скорости спутника в перигее и апогее эллиптической орбиты, имеем:

r₁υ₁ = r₂υ₂ (3)

(4)

Выражая υ₂ из (3) и подставляя в (4), получим:

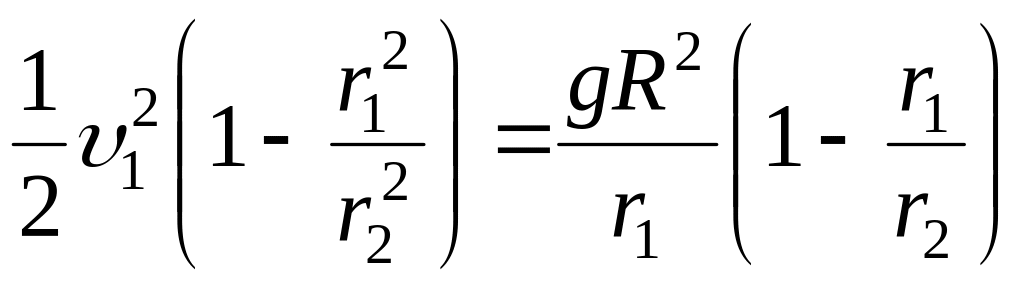(5)

Замечая, что есть квадрат скорости спутника на круговой орбите радиусом r₁, из уравнения (5) получаем

Отсюда большая полуось эллипса

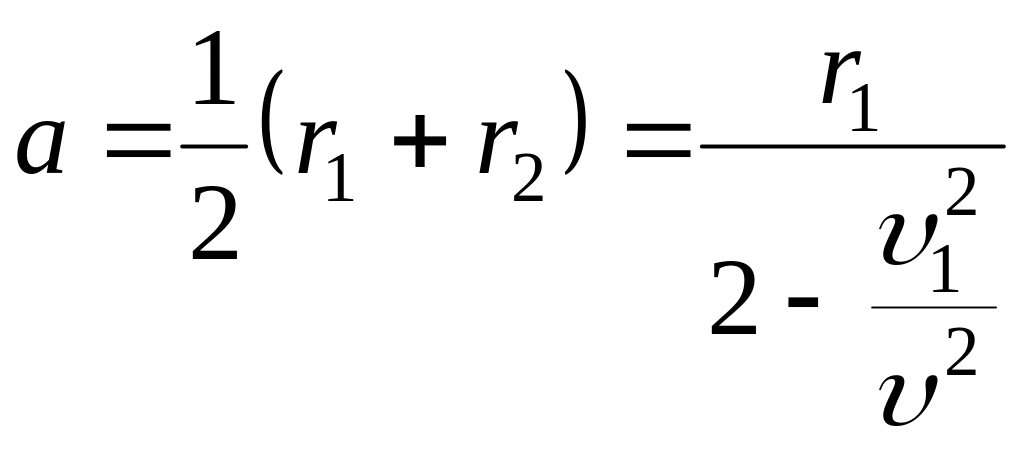
Поскольку по условию добавочная скорость Δυ много меньше скорости орбитального движения υ, то

Теперь для большой полуоси имеем . Подставим полученное выражение для а в уравнение третьего закона Кеплера (2). Возведя отношение в куб и учитывая, что , находим

(6)

Сравнивая (1) и (6), видим, что

(7)

Итак, если мы хотим, чтобы встреча спутников произошла через один оборот, то идущему впереди спутнику нужно сообщить добавочную скорость Δυ, определяемую соотношением (7).

Чтобы встреча произошла через n оборотов, нужно сообщить добавочную скорость .

Таким образом, мы можем израсходовать тем меньше топлива для совершения манёвра, чем больше времени согласны ждать встречи.

Не забудьте, что после завершения манёвра сближения, для того чтобы перевести спутник снова на круговую орбиту, придётся погасить сообщённую ему добавочную скорость, т.е. ещё раз включить двигатель.

Второй случай, когда требуется «догнать» идущий впереди спутник рекомендуется рассмотреть самостоятельно. Вы получите такое же выражение для Δυ.

Ответ: .