О сновные определения и формулы

Основой теории относительности являются два постулата, сформулированные А. Эйнштейном.

Первый постулат – принцип относительности: все физические явления в любых ИСО при одинаковых начальных условиях протекают одинаково. Принцип относительности Эйнштейна является обобщением механического принципа относительности на все явления физики.

Второй постулат – принцип инвариантности скорости света в вакууме: скорость света в вакууме не зависит от скорости движения источника света и наблюдателя и одинакова во всех инерциальных системах отсчёта (c = 3·10⁸ м/с = сonst).

В соответствии с двумя постулатами специальной теории относительности между координатами и временем в двух исо k и k’ существуют соотношения, которые называются преобразованиями Лоренца.

Закон сложения скоростей: если материальная точка M (рис. 12.1) движется вдоль оси OX, а следовательно, и OX’ в инерциальных системах K и K’ и имеет в этих системах отсчёта скорости, равные соответственно u и u’, то

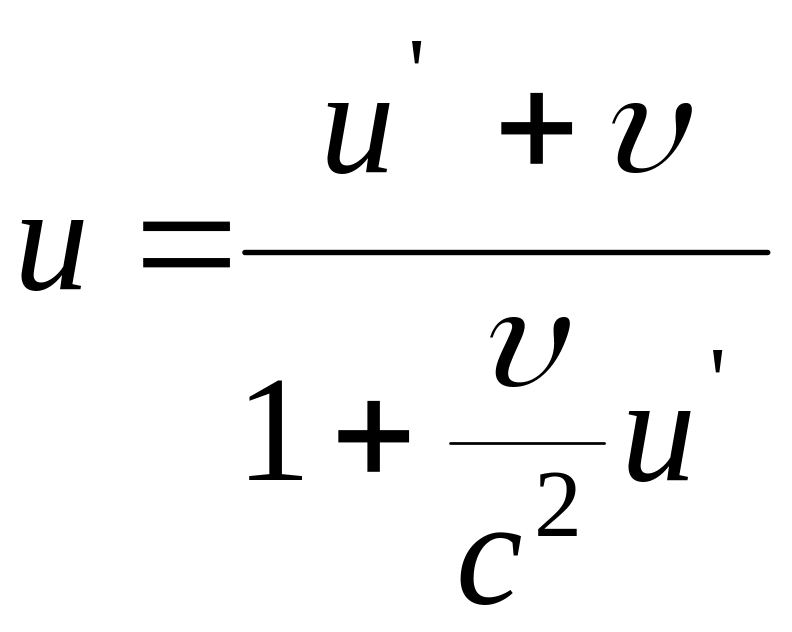
где υ – скорость движения системы K’ относительно K.

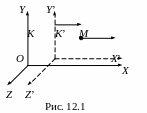
Длина тела в различных ИСО. Длина тела в системе K’, где оно покоится, называется собственной длиной. Из преобразований Лоренца следует, что длина тела (масштаб) меняется при переходе от одной ИСО к другой и определяется соотношением

где l- длина тела в ИСО, относительно которой тело движется; l₀- длина тела в ИСО, относительно которой оно покоится.

Длительность событий также относительна. Промежуток времени Δt, измеренный в системе отсчёта, относительно которой тело неподвижно, называется собственным временем. Собственное время отсчитывается по часам, движущимся вместе с системой отсчёта. Из преобразований Лоренца следует, что

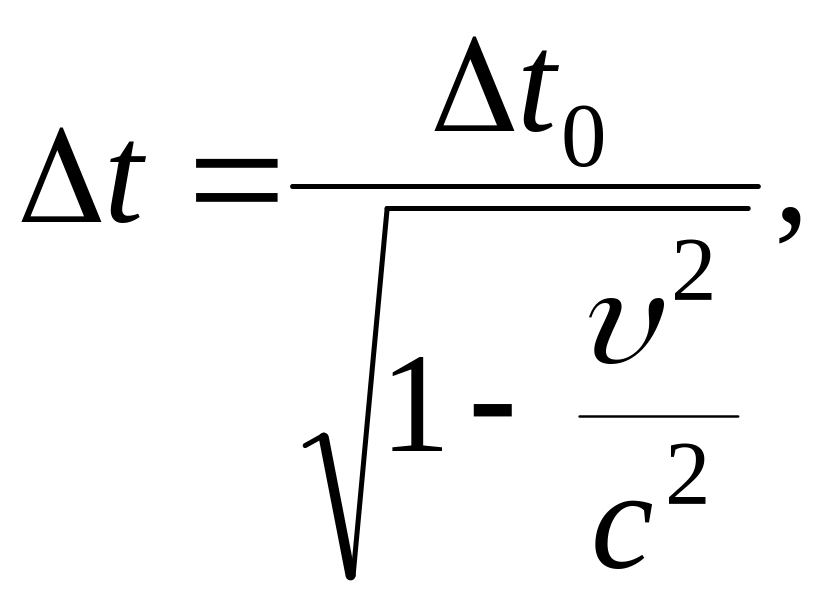
где t – лабораторное время – промежуток времени, измеренный в ИСО, относительно которой тело движется.

Закон взаимосвязи массы и энергии выражается формулой А. Эйнштейна:

W = m₀c² + W_k = mc²

где - релятивистская масса частицы, она зависит от скорости υ, с которой частица движется в данной системе отсчёта.

При условии υ << c релятивистская масса принимает значение массы покоя, то есть m = m₀.

Полная энергия частицы равна произведению её релятивистской массы на квадрат скорости света в вакууме.

W = mc²

Величина W₀ = m₀c² определяет максимальную величину энергии, которая могла быть извлечена из данного тела в ИСО, относительно которой оно покоится.

Между полной энергией W и релятивистским импульсом р в специальной теории относительности существует связь

где p = mυ – релятивистский импульс частицы, движущейся со скоростью υ.

Импульс р и кинетическая энергия W_k связаны соотношением

.

Примеры решения задач.

1. Релятивисткая частица распадается на два одинаковых «осколка», каждый из которых имеет массу покоя m. Один из «осколков» неподвижен относительно лабораторной системы отсчёта, а другой движется со скоростью υ = 0,8c. Какую скорость u и массу покоя M имела частица до распада?

Р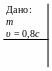 ешение.

Согласно законам сохранения энергии и импульса должны выполняться соотношения:

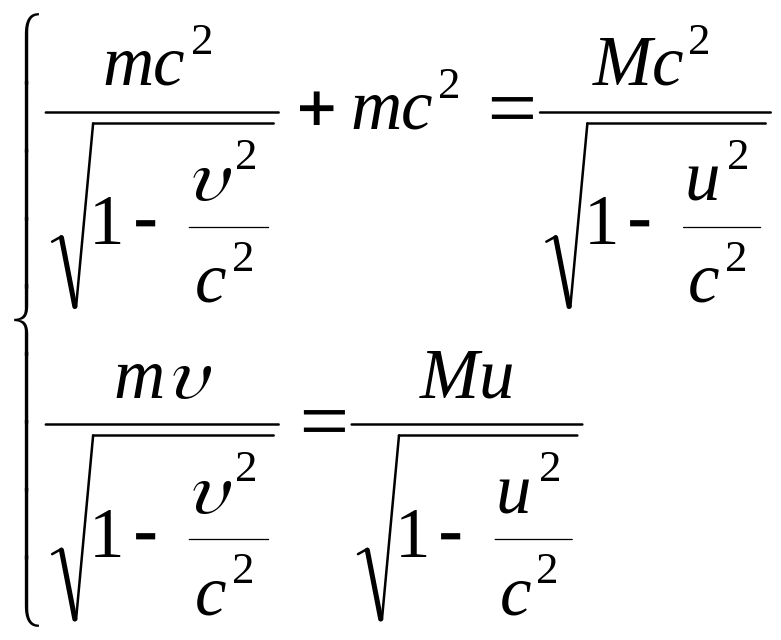
Разделив почленно второе уравнение на первое, получим:

Это скорость центра масс. Подставляя данное значение в любое из уравнений системы, получим:

.

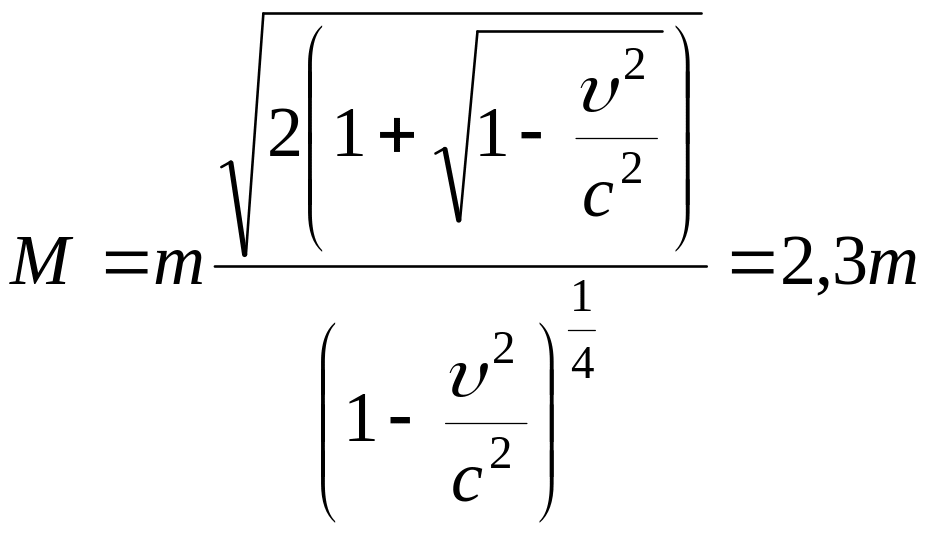Разумеется при υ << c мы получили бы M ≈ 2m. При реальных распадах нестабильных ядер и элементарных частиц расчёты усложняются: заметную часть энергии могут уносить кванты электромагнитного излучения и нейтрино.

Ответ: u = 0,5c; M = 2,3m.

2. Определить скорость электрона, имеющего кинетическую энергию равную 1,53 МэВ.

Р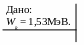 ешение.

Кинетическая энергия в инерциальных системах отсчёта определяется по формуле:

.

Откуда можем получить:

,

где энергия покоя электрона величина постоянная и равна:

МэВ.

Подставляя полученные данные имеем:

и тогда скорость электрона:

υ = c ∙ β = 3 ∙ 10⁸ ∙ 0,97 = 2,9 ∙ 10⁸м/с.

Ответ: υ = 2,9 ∙ 10⁸м/с.

3. Какую ускоряющую разность потенциалов должен пройти протон, чтобы его продольный размер стал в два раза меньше поперечного?

Р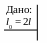 ешение.

Используя определение работы и способ её вычисления при перемещении заряда в электрическом поле, а также формулу определения кинетической энергии в релятивисткой механике, можем записать:

,

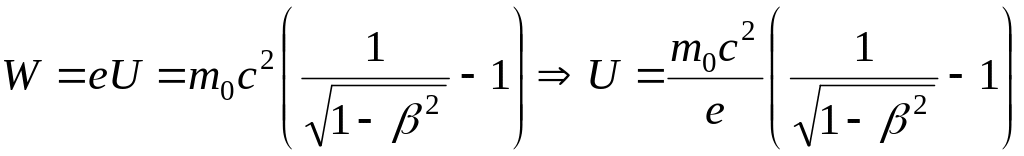но, используя условие: , подставив в предыдущую формулу с учётом исходных данных, получим:

В.

Ответ: U = 9,39 ∙ 10⁸В.

4. Два ускорителя выбрасывают частицы навстречу друг другу со скоростями 0,9c. Определить относительную скорость сближения частиц.

Р ешение.

Для решения воспользуемся законом сложения скоростей в релятивисткой механике:

Из условия υ = – u = 0,9c. Тогда: .

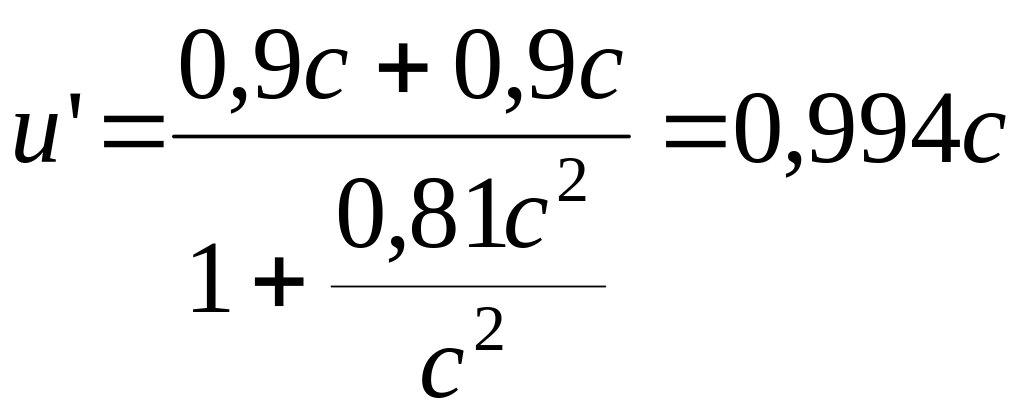Ответ: u’ = 0,994c.

5. Найти скорость мезона, если его полная энергия в 10 раз больше покоя.

Р ешение.

Используя исходные данные, из формулы полной энергии выразим кинетическую энергию через энергию покоя:

W = W_k + W₀ → W_k = W – W₀ = 10W₀ – W₀ = 9W₀.

С другой стороны кинетическую энергию можем определить по формуле вытекающей из определения полной энергии:

Подставляя в неё имеющиеся данные, выражаем и определяем скорость мезона:

м/с.

Ответ: υ = 2,985 ∙ 10⁸м/с.

6. Мю – мезон, рождающийся в верхних слоях атмосферы, пролетает до распада 6000м. Определить с какой скоростью летит мю – мезон, если его собственное время жизни 2,2 ^. 10 ^–6 с.

Р ешение.

Скорость определим из уравнения пути при равномерном движении:

,

где время определим по формуле длительности событий в инерциальных системах отсчёта: 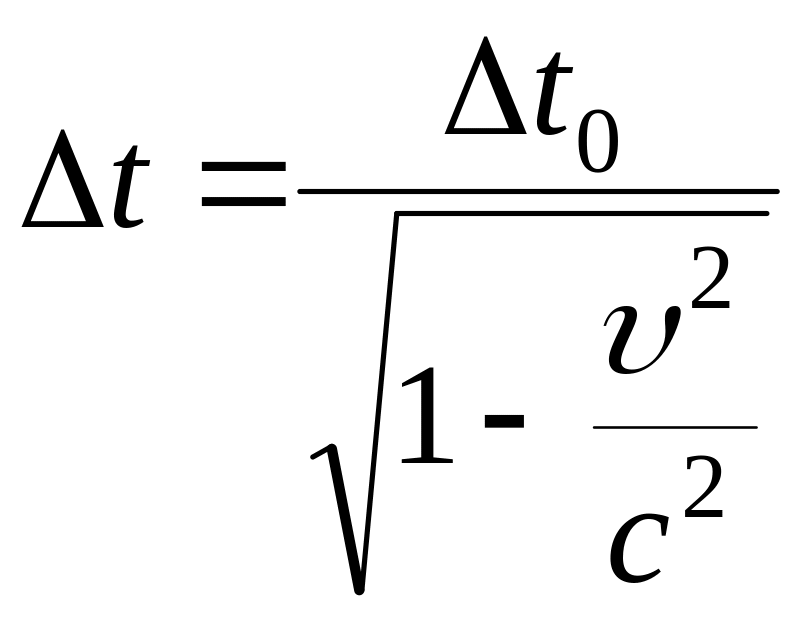. Тогда можем записать:

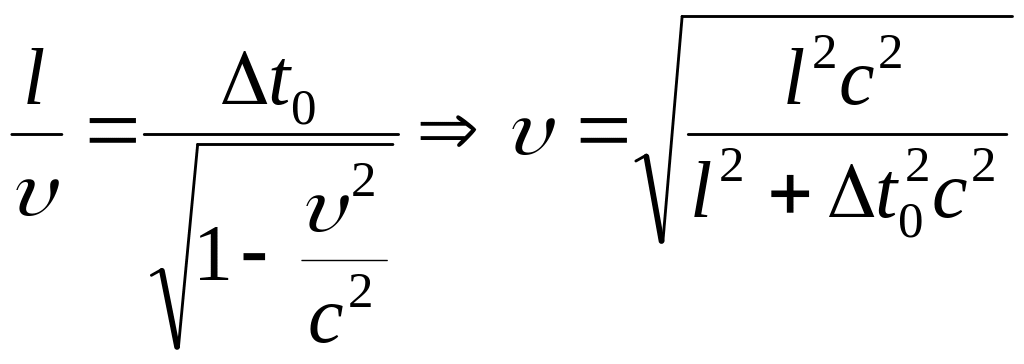
Подставляя числовые значения, получим:

.

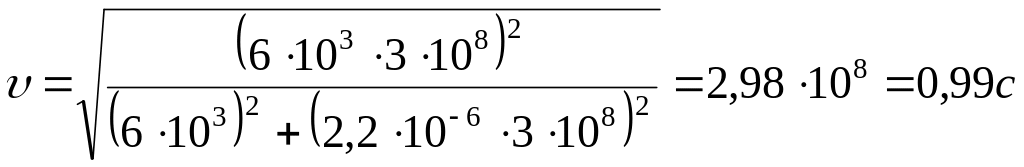Ответ: υ = 0,99c.

7 . Как зависит период обращения релятивисткого протона в циклотроне от скорости протона υ? Величина индукции магнитного поля равна B.

Р ешение.

При движении в циклотроне на протон действует сила Лоренца F = eB υ. Эта сила сообщает протону центростремительное ускорение , где R - радиус окружности по которой движется протон. Из соотношения находим

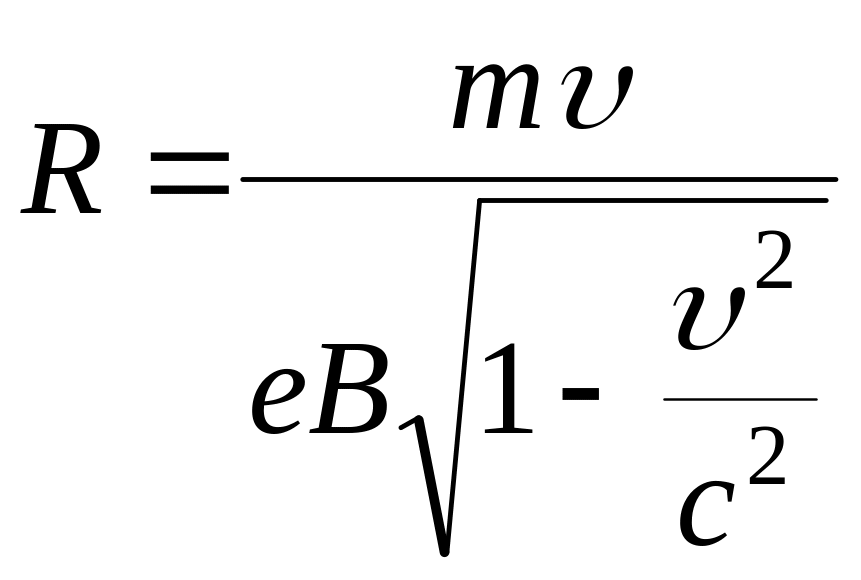
Период обращения по окружности

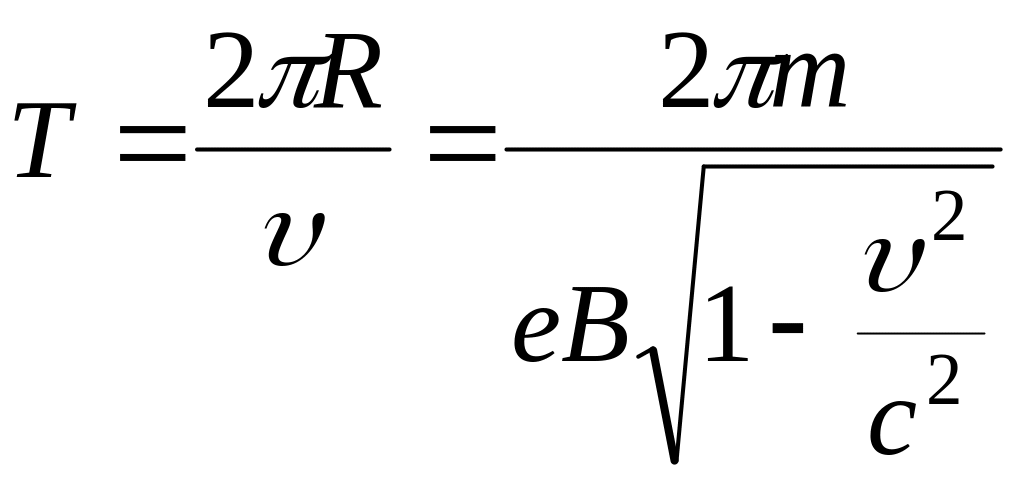
При υ << c период не зависит от скорости частицы: . График зависимости T(υ) приведён на рисунке 12.2.

Ответ: .
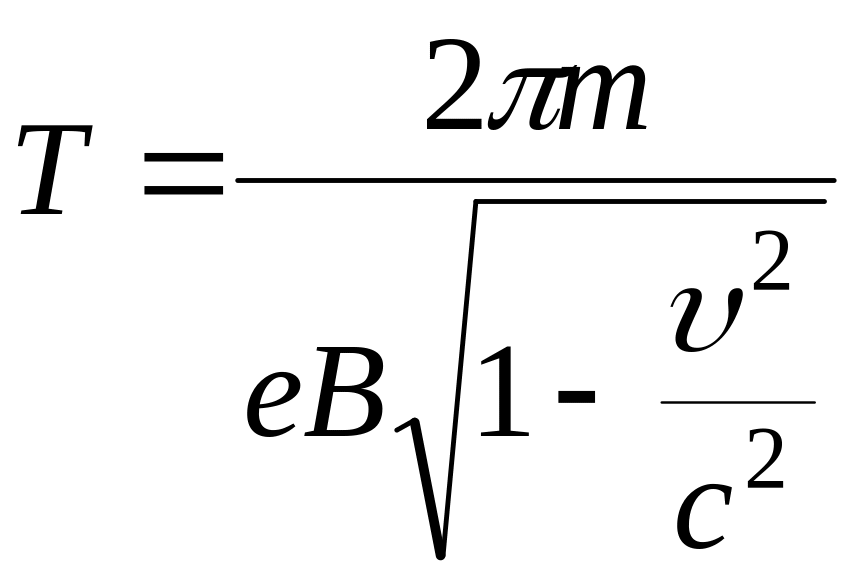