Примеры решения задач.

1. Два тела массами m₁ = 1 кг и m₂ = 2 кг связаны невесомой нитью и движутся по горизонтальной поверхности (на Земле) под действием силы F = 10 Н, направленной горизонтально и приложенной к телу m₁. Определить силы, действующие на каждое тело, если коэффициент трения между каждым телом и поверхностью равен μ = 0,05 (рис. 4.1).

Решение.

1 ) Тело m₁ взаимодействует с Землей, нитью и телом m₂. С Землей тело m₁ взаимодействует по закону всемирного тяготения, следовательно, на него действует сила, направленная вниз и равная .

2) Тело m₁ взаимодействует с Землей упруго, появляется упругая сила реакции опоры , направленная вверх.

3) В результате взаимодействия тела m₁ с Землей появляется сила трения F_mp1 = μN₁.

4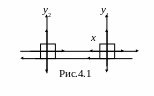 ) Тело m₁ взаимодействует с нитью упруго: на него действует сила натяжения нити , направленная влево (нить невесома, поэтому сила взаимодействия между нитью и телом равна 0).

5) На тело m₁ действует сила .

Рассуждая также, можно показать, что на тело m₂ действуют четыре силы: упругая сила натяжения нити , сила тяжести , упругая сила реакции опоры сила трения F_mp1 = μN₂.

На основании II закона Ньютона можно видеть, что силы (так как нить невесома, масса ее равна 0, т.е. ).

Запишем для каждого тела II закон Ньютона:

Выберем систему координат для решения векторных уравнений. Система координат выбирается произвольно, исходя из условий задачи и для каждого тела отдельно.

Возьмем направление оси х в направлении ускорения (слева направо). Ось у направлена вертикально.

Найдем проекции всех сил на оси координат.

Ось х: I тело: F_x = F; F_нх = –F_н1; F_mpx = –F_mp1; N_1x = 0; m₁g_x = 0.

II тело: F_нх = –F_н2; F_mpx = –F_mp2; N_2x = 0; m₂g_x = 0.

Ось у: I тело: N_1y = N₁; m₁g_y = – m₁g.

II тело: N_2y = N₂; m₂g_y = – m₂g.

Составим систему уравнений движения для каждого тела.

I тело:

(1)

II тело:

(2)

Найдем силу трения F_mp1 и F_mp2:

Н.

Н.

Определим ускорение системы тел, подставив F_mp1 и F_mp2 в уравнения (1) и (2):

, так как нить невесома. Сложив эти два уравнения, получим выражение

;

Зная ускорение, найдем силу натяжения нити, например,

Н.

Ответ: F_mp1 = 0,49Н; F_mp2 = 0,98Н; F_н1 = F_н2 ≈ 6,6Н.

2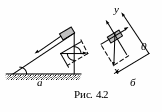 . Тяжёлое тело находится на вершине наклонной плоскости на грани скольжения (рис. 4.2а). За какое время тело спустится с наклонной плоскости, если она станет двигаться в горизонтальном направлении с ускорением a = 0,5м/с²? Длина наклонной плоскости l = 1м, угол наклона её к горизонту равен α = 30⁰.

Р ешение.

В задаче рассматриваются два состояния тела: первое, когда оно находится на грани скольжения, второе – в равноускоренном движении.

Условие о нахождении тела на грани скольжения имеет вспомогательное значение. Оно позволяет определить коэффициент трения скольжения μ между телом и плоскостью.

1. Для определения μ (это самостоятельная задача) нужно составить основное уравнение динамики с учётом того, что ускорение тела равно нулю.

На тело находящееся на наклонной плоскости, действуют сила тяжести, равная , реакции опоры и сила трения .

Выберем систему отсчёта – Землю и свяжем с ней прямоугольную систему координат. Ось Ох направим вдоль наклонной плоскости вниз, ось Оу – перпендикулярно наклонной плоскости вверх. Находим проекции сил на оси Ох и Оу. Они равны соответственно:

mgsinα, – F_mp, – mgcosα и N

Под действием приложенных сил тело находится на наклонной плоскости в равновесии на грани скольжения, следовательно, основное уравнение динамики в проекциях на оси координат будет иметь вид:

mgsinα – F_mp = 0 и N – mgcosα = 0, причём F_mp = μN.

Решая уравнения совместно относительно коэффициента трения, находим:

μ = tgα.

Полученная формула для коэффициента трения скольжения имеет место лишь для случая, когда тело равномерно скользит по наклонной плоскости или находится на грани скольжения. Если угол наклона плоскости больше или меньше предельного, пользоваться этой формулой нельзя.

2. Сообщая горизонтальное ускорение наклонной плоскости, мы тем самым как бы вынимаем её из-под груза и уменьшаем силу давления плоскости на груз в направлении нормали. В результате сила нормального давления , а стало быть, и сила трения, препятствующая скольжению груза по плоскости, уменьшаются: mgsinα станет больше F_mp и груз начнёт перемещаться относительно плоскости с некоторым ускорением .

Движение груза относительно неподвижного тела отсчёта (Земли) будет сложным, оно складывается из двух прямолинейных движений – переносного с ускорением (вместе с наклонной плоскостью) и относительного ускорения вдоль наклонной плоскости.

На груз, находящийся в ускоренном движении, действуют такие же силы, что и при его равновесии: , и (рис. 4.2б), но модули сил и будут другими. Проецируем силы на координатные оси Ох и Оу. Проекции сил равны соответственно

mgsinα, – F_mp, – mgcosα и N,

проекции относительного и переносного ускорений равны:

a₀, 0, – acosα и – sin α.

Под действием приложенных сил тело ускоренно движется вниз по наклонной плоскости с некоторым ускорением относительно Земли и в направлении, перпендикулярном наклонной плоскости вместе с наклонной плоскостью с ускорением, проекция которого на ось Оу равна - asinα.

Основное уравнение динамики для проекций на ось Ох имеет вид:

mgsinα – μN₁ = ma₁. (1)

Перемещение тела с ускорением можно рассматривать как состоящее из двух: движения относительно наклонной плоскости с ускорением и движения в противоположную сторону вместе с плоскостью с ускорением, модуль которого acosα. Поэтому

a₁ = a₀ – acosα (2)

Основное уравнение динамики для проекций на ось Оу имеет вид:

N₁ – mgcos α = – masin α (3)

В заключение остаётся записать кинематическое уравнение, обратив внимание на то, что относительно наклонной плоскости тело движется с ускорением :

(4)

Уравнения (1) – (4) содержат четыре неизвестные величины: a₁, a₀, N₁ и t. Решая их совместно, для времени спуска тела с наклонной плоскости, получим:

с.

Ответ: t = 1,87с.

3. К концам лёгкой нити, перекинутой через блок, укрепленный на динамометре, подвешены два груза массами m₁ = 0,1кг и m₂ = 0,2кг. Определите ускорение грузов, натяжение нити и показание динамометра при условии, что блок вместе с грузами поднимается на динамометре вверх с ускорением a_n = 1,2м/с². Массой блока и динамометра пренебречь.

Р ешение.

Решение задач динамики, в которых тела одновременно участвуют в двух ускоренных движениях – относительном и переносном, принципиально ничем не отличаются от задач, где рассматривается одно движение. Особое внимание здесь нужно обратить на то, что в основном уравнении динамики под всегда подразумевается полное (абсолютное) ускорение относительно неподвижного тела отсчёта – Земли и его приходится представлять как сумму относительного и переносного ускорений:

.

Е сли в сложном движении участвуют не одно, а несколько тел (как, например, в данной задаче), то независимо от того, требуется или нет определять внутренние силы системы, движение каждого тела необходимо рассматривать отдельно, поскольку они имеют разные абсолютные ускорения.

В данной задаче грузы перемещаются относительно блока (относительное движение) и одновременно с этим поднимаются вверх вместе с блоком (переносное движение). Делаем схематический чертёж (рис.4.3), где прежде всего проставляем векторы относительного ускорения и переносного .

На левый груз действуют сила тяжести и сила натяжения нити . Под действием этих сил груз движется вертикально вверх с некоторым ускорением относительно неподвижного тела отсчёта – Земли, поэтому

T – m₁g = m₁a₁ (1)

Модуль ускорения связан с модулем относительного и переносного ускорений соотношением:

a₁ = a₀ + a_n, (2)

поскольку оба эти ускорения направлены вверх.

На правый груз также действуют две силы: и , однако сразу установить, какая из них больше, какая меньше, и определить тем самым направление полного ускорения этого груза нельзя. В зависимости от значений величин m₁g и m₂g при заданном а больший груз может иметь относительно Земли ускорение, направленное или вверх (при T > m₂g), или вниз (если T < m₂g), или даже находиться в состоянии покоя (при T = m₂g).

Предположим, что направление полного ускорения a₂ совпадает с направлением относительного движения, т.е. m₂g > T и вектор направлен вниз (груз опускается, приближаясь к Земле). Тогда основное уравнение динамики в проекциях на ось, направленную в сторону предполагаемого движения груза, будет иметь вид:

m₂g – T = m₂a₂ (3)

При нашей договорённости о направлении относительное ускорение должно быть больше переносного (a₀ > a_n), и, следовательно,

a = a₀ – a_n (4)

Блок взаимодействует с тремя телами: Землёй, динамометром и нитью. Основное уравнение динамики (при условии, что масса блока ничтожно мала) даёт:

N – 2T = 0 (5)

Решая уравнения (1) – (5) совместно относительно искомых неизвестных величин, находим:

м/с²;

м/с²;

Н;

N = 2T = 2,94Н.

Ускорение a₂ получилось положительным. Это значит, что мы выбрали правильное направление ускорения (груз движется вниз).

Ответ: a₁ = 4,87м/с²; a₂ = 2,47м/с²; Н; N = 2,94Н.

4. Небольшая шайба движется по наклонной плоскости, коэффициент трения которой μ = tgα, где α - угол наклона плоскости к горизонту. Найти зависимость скорости υ шайбы от угла φ между вектором скорости и осью х (рис. 4.4), если в начальный момент υ = υ₀ и φ = π/2.

Р ешение.

Ускорение шайбы вдоль плоскости определяется составляющей силы тяжести на эту плоскость F_x = mgsinα и силой трения F_mp = μmgcosα. В нашем случае μ = tgα, поэтому

F_mp = F_x = mgsinα

Найдём проекции ускорения на направление касательной к траектории и на ось х:

О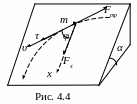 тсюда видно, что a_τ = – a_x, а это значит, что скорость υ и её проекция υ_x различаются лишь на некоторую постоянную С, не зависящую от времени, т.е. υ = – υ_x + C, где υ_x = υcosα. Постоянную С находим из начального условия υ = υ₀, откуда C = υ₀. В результате получим:

.

С ростом времени φ → 0 и .

Ответ: .

5. Тяжёлый шарик подвешен на нити длиной l. Нить равномерно вращается в пространстве, образуя с вертикалью угол α (конический маятник). Сколько оборотов делает шарик за время t? Решите задачу при условии, что конический маятник установлен в ракете, поднимающейся вертикально вверх с ускорением .

Р ешение.

При вращении нити на шарик действуют две силы: со стороны Земли сила тяжести, равная , и со стороны нити сила натяжения . Под действием приложенных сил шарик движется равномерно в горизонтальной плоскости по окружности радиусом R с некоторой скоростью υ (рис. 4.5а). Это возможно лишь при условии, что равнодействующая сил и оказывается направленной перпендикулярно скорости к центру окружности О и, следовательно, сообщает шарику нормальное ускорение

, где

Изобразив силы, действующие на шарик, составляем основное уравнение динамики в проекциях по нормали к окружности:

(1)

Чтобы найти из этого соотношения какую-либо величину, в частности модуль суммы , нужно определить длину диагонали параллелограмма, построенного на векторах и . Сделать это можно различными способами.

а) Сложить силы и по правилу параллелограмма и найти его диагональ, зная, что равнодействующая этих сил направлена по радиусу. Как видно из рисунка а.

.

б) Разложить вектор по направлению нити и радиуса вращения на составляющие и . Из рисунка б видно, что модули составляющих равны . Поскольку нить нерастяжима и вдоль неё ускорения нет, то согласно второго закона Ньютона и, стало быть, .

Следовательно, составляющая силы тяжести равна равнодействующей всех сил, приложенных к шарику, т.е. она сообщает ему нормальное ускорение.

в) Для вычисления равнодействующей сил и можно использовать метод проекций. Выберем для этого систему отсчёта, например Землю, и связанную с ней систему координат. Ось Ох направим по радиусу вращения, ось Оу – вертикально вверх (рис.4.5в). Проекции этих сил по осям равны T sinα, T cosα и – mg.

Так как по вертикальному направлению скорость шарика не изменяется, то основное уравнение динамики для проекций на ось Оу даёт:

T cosα – mg = 0

По оси Ох есть только одна проекция T sinα, которую можно рассматривать как проекцию всех сил, приложенных к шарику.

Сравнивая все три результата, нетрудно заметить, что в данном примере модуль равнодействующей силы равен:

и согласно (1) уравнение второго закона Ньютона в скалярной форме можно представить в одном из трёх видов:

.

Какое из этих уравнений нужно использовать в том или ином конкретном случае, зависит от вопроса задачи и исходных данных.

Если не задана масса частицы, как, например, в нашем случае, уравнение второго закона удобно записать в первой форме:

(2)

Составив уравнение динамики, записываем дополнительные условия:

, (3)

где N - число оборотов шарика и R = l sinα (4)

Исключая из уравнений (2) – (4) υ и R и, решая их относительно N, получим:

.

2. Если конический маятник установлен в ракете, поднимающейся вертикально вверх с ускорением , число сил, действующих на шарик, остаётся тем же. Однако сила натяжения действует на шарик не так, как в первом случае; она не только Совместно с силой ) обеспечивает движение шарика по кругу, но и сообщает ему ускорение , равное ускорению ракеты. Так как шарик участвует в двух ускоренных движениях (равномерном по окружности и прямолинейном вверх), для нахождения связи между действующими силами и и ускорениями нужно составить основное уравнение динамики в проекциях на оси прямоугольной системы координат Оху, учитывая, что проекции ускорений на эти оси равны а и . Для оси Ох будем иметь:

, (5)

для оси Оу:

T cosα – mg = ma (6)

Решая совместно (3), (5) и (6) относительно N, получим:

Анализируя ответ, можно заметить следующее: 1) в системе, поднимающейся ускоренно вверх, явление протекает так, как если бы ускорение свободного падения увеличилось на а; 2) по мере увеличения числа оборотов в единицу времени угол α увеличивается и становится равным 90⁰ при бесконечно большой скорости вращения. Из этого следует, что груз на нити в горизонтальной плоскости вращаться не может.

Ответ: 1) ; 2) .