4 Ускорение кориолисово

Кориолисовым или поворотным ускорением называется составляю­щая абсолютного ускорения точки в сложном движении, равная удвоен­ному векторному произведению угловой скорости переносного вращения на относительную скорость точки:

(13.13)

Кориолисово ускорение характеризует:

1) изменение модуля и направления переносной скорости точки вследствие ее относительного движения;

2) изменение направления относительной скорости точки вследствие вращательного переносного движения.

Например, если человек идет равномерно вдоль радиуса равно­мерно вращающейся платформы, то его относительной скоростью является скорость его движения вдоль радиуса, а переносной — ско­рость той точки платформы, где он находится в данный момент (рис. 13.6).

Пусть в момент времени t человек занимает положение М, а в момент t + Δt - положение M₁.

Так как относительное движение равномерное и прямолинейное, то относительное ускорение человека . Однако за время Δt относительная скорость изменяется по направлению от до , вслед­ствие вращения подвижной системы (платформы).

Рис. 13.6 Рис. 13.7

За время Δt происходит изменение модуля переносной скорости от до вследствие относительного перемещения человека из точки М в точку M₁ и ее направления. Указанные изме­нения и вызывают появление кориолисова ускорения. Модуль кориолисова ускорения определяется как модуль вектор­ного произведения (13.13):

. (13.14)

Кориолисово ускорение равно нулю в трех случаях:

1) если , т. е. в случае поступательного переносного движения или в моменты обращения в нуль угловой скорости непоступатель­ного переносного движения;

2) если , т. е. в случае относительного покоя точки или в моменты равенства нулю относительной скорости движущейся точки:

3) если , т.е. в случае, когда или ; иначе, когда относительная скорость точки параллельна оси переносного вращения, как, например, при движении точки М вдоль образующей цилиндра, вращающегося вокруг своей оси (рис. 13.7). Направление кориолисова ускорения определяется по правилу вектор­ного произведения.

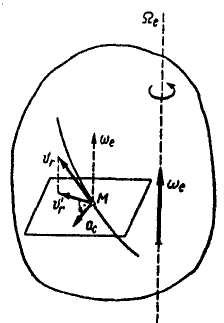
Рис. 13.8 Рис. 13.9

IIycть точка М движется со скоростью относительно тела, вращающегося вокруг оси с угловой скоростью (рис. 13.8). Построив условно вектор в точке М, направляем кориолисово ускорение по перпендикуляру к плоскости векторов и в ту сторону, откуда поворот вектора к скорости на наименьший угол виден происходящим в сторону, обратную вращению часовой стрелки.

Для определения направления кориолисова ускорения удобно поль­зоваться правилом Жуковского: чтобы найти направление кориолисова ускорения, следует спроецировать относительную скорость точки на плоскость, перпендикулярную оси переносного вращения, и повернуть эту проекцию в той же плоскости на 90° в сторону переносного вращения (рис. 13.9).

Действительно, полученное направление (рис. 13.9) перпендику­лярно плоскости треугольника, образованного скоростью и ее проекцией , а эта плоскость совпадает с плоскостью векторов и (рис. 13.8). Если , то sin ( , ) = 1, тогда

(13.15)

В этом случае три вектора , , взаимно перпендикулярны (рис. 13.10). Этот случай определения направления кориолисова ускорения возможен при относительном движении точки в плоскости, перпен­дикулярной оси переносного вращения.

Рис. 13.10 Рис. 13.11

Для иллюстрации правила Жуковского рассмотрим несколько при­меров определения модуля и направления кориолисова ускорения.

Предположим, например, что диск вращается вокруг оси, перпенди­кулярной его плоскости в сторону, обратную вращению часовой стрелки с угловой скоростью , а по хорде диска KL движется точка М (рис. 13.11).

Рис. 13.12 Рис. 13.13

Определим модуль и направление кориолисова ускорения точки М в положении, указанном на рисунке, если относительная скорость точки в этот момент равна . Так как точка движется в плоскости диска, перпендикулярной его оси вращения, то sin( , )=1 и модуль кориолисова ускорения

.

Направление корнолисова ускорения получаем, повернув в пло­скости диска вектор против вращения часовой стрелки на угол 90°.

Определим теперь модуль и направление кориолисова ускорения точки М, движущейся с относительной скоростью по образую­щей кругового конуса под углом МОА = а от его вершины к основа­нию (рис. 13.12). Конус вращается вокруг своей оси с угловой ско­ростью в направлении, указанном на рисунке.

Отложив вектор угловой скорости переносного вращения по оси этого вращения, находим .

Определяем модуль кориолисова ускорения точки М:

Чтобы найти направление кориолисова ускорения, проецируем отно­сительную скорость точки на плоскость, перпендикулярную оси враще­ния конуса. Проекция относительной скорости направлена по пря­мой СК, совпадающей с радиусом СМ. Повернув эту проекцию на угол 90^о но направлению вращения конуса, установим, что кориолисово ускорение направлено по касательной к окружности радиусом СМ в сторону вращения конуса.

Кориолисовым ускорением обладают точки (тела), движущиеся по поверхности Земли, например частицы воды в реках, поезда, авто­мобили и т.д.