Угловая скорость вращения колеса

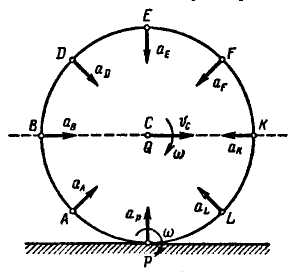
Рис. 12.12

Центр колеса движется равно­мерно по прямой; следовательно, его ускорение т.е. центр колеса является мгно­венным центром ускорений.

Так как колесо вращается равномерно, то ускорения всех точек колеса равны центростремительным ускорениям этих точек в их вра­щательном движении вокруг мгновенного центра ускорения. Например, ускорения точек обода определяются так:

Ускорение каждой точки колеса направлено к мгновенному центру ускорений. В рассмотренном примере наглядно видно, что мгновенный центр скоростей Р и мгновенный центр ускорений Q являются раз­личными точками плоской фигуры. Мгновенный центр скоростей, не имея в данный момент скорости, имеет ускорение , а мгновенный центр ускорений, не имея в данный момент ускорения, имеет ско­рость .

С л у ч а й II. Известны модуль и направление ускорения какой-либо точки А плоской фигуры , а также угловая скорость и угловое ускорение фигуры.

Определим положение мгновенного центра ускорений в частных случаях, зависящих от значений и .

1. Неравномерное вращение: . В этом случае мгновенный центр ускорений находится на отрезке, составляющем с направлением ускорения угол , который отложен от ускорения точки в сторону на расстоянии от точки А, равном

.

На рис. 12.13 показан случай ускоренного вращения плоской фигуры, а на рис. 12.14 — случай замедленного вращения.

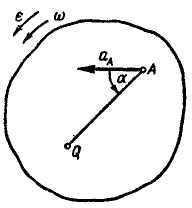
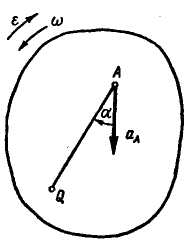
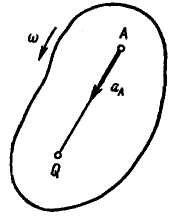
Рис. 12.13 Рис. 12.14 Рис. 12.15

Ускорение любой другой точки плоской фигуры можно определить по формуле (12.4). Как видно, направление вращения на построение угла не влияет и угол всегда откладывается от направления ускорения в сторону .

2. Равномерное вращение: (также момент, когда при неравномерном вращении) (рис. 12.15). В этом случае

и

т. е. ускорения всех точек направлены к мгновенному центру ускорений. Расстояние от точки до мгновенного центра ускорений определяется по формуле:

(12.6)

3. Момент, когда угловая скорость становится равна нулю: . В этом случае

т.е. ускорения всех точек направлены перпендикулярно отрезкам, соединяющим эти точки с мгновенным центром ускорений (рис. 12.16). Расстояние от точки до мгновенного центра ускорений определя­ется по формуле

(12.7)

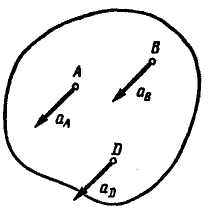
Рис. 12.16 Рис. 12.17

Угловая скорость фигуры обычно обращается в нуль при измене­нии направления вращения фигуры.

4. Момент, когда угловая скорость и угловое ускорение становятся равными нулю при непоступательном движении: . В этом случае ускорения всех точек плоской фигуры в данный момент геометрически равны, так как ускорение любой точки равно ускорению полюса (рис. 12.17) по формулам :

.

С л у ч а й III. Известны модули и направления ускорений двух точек плоской фигуры. Допустим, что известны ускорения точек А и В плоской фигуры и (рис. 12.18).

Примем точку А за полюс, тогда

Построим при точке В параллелограмм ускорений по заданной диагонали и одной из сторон . Другая сторона параллелограмма определит ускорение во вращении точки В фигуры вокруг полюса А. Ускорение составляет угол с отрезком АВ, соединяющим точку В с полюсом А.

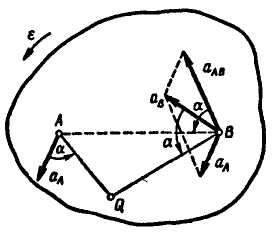
Рис. 12.18

Отсчитывая полученный угол α от ускорения к отрезку АВ, получаем направление , в данном случае противоположное направле­нию вращения часовой стрелки. Определив угол α и направление , отложим этот угол от ускорений точек А и В по направлению . Две полученные полупрямые продолжим до пересечения в точке Q, которая и будет мгновенным центром ускорений.

Этот способ определения положения мгновенного центра ускорений не требует определения угла α путем вычислений. Если положение мгновенного центра ускорений по этому способу определяется графи­чески, то ускорения точек должны быть отложены в масштабе по их истинным направлениям.

Рассмотрим случаи, когда ускорения точек плоской фигуры парал­лельны. Положение мгновенного центра ускорений в этом случае определяется на основании того, что:

1) модули ускорений точек пропорциональны длинам отрезков, соединяющих точки с мгновенным центром ускорений:

.

2) ускорения точек составляют с отрезками, соединяющими точки с мгновенным центром ускорений, один и тот же угол .

На рис. 12.19 и 12.20 выполнено построение для случая , т. е. .

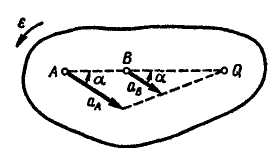
Рис. 12.19 Рис. 12.20

Рис. 12.21 и 12.22 соответствуют случаю α=90^о:

.

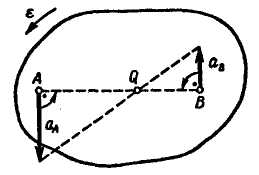
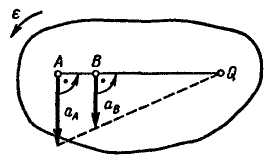
Рис. 12.21 Рис. 12.22

На рис. 12.23 и рис. 12.24 построен мгновенный центр ускорений для случая

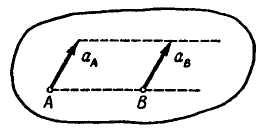
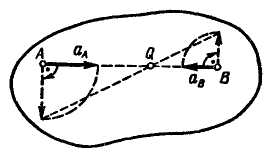
Рис. 12.23 Рис. 12.24

.

В случае (рис. 12.23) мгновенный центр ускорений находится в бесконечности, а ускорения всех точек плоской фигуры геометри­чески равны.