На этом основании

В этом заключается первое следствие теоремы об ускорениях точек плоской фигуры.

Проекции ускорений на ось, направленную из полюса, могут иметь знаки плюс и минус.

Из следствия вытекает, что алгебраическая величина проекции меньше , а абсолютное значение может и пре­вышать при большом центростремительном ускорении . Про­екции ускорений точки А и полюса О на ось х равны в том случае, если т. е. при

Проведем через конец ускорения полюса , отложенного в точке А, прямую, перпендикулярную оси х. Эта прямая представляет собой годограф возможных ускорений точки плоской фигуры при т. е. при , и является границей, за которую не могут выходить концы возможных ускорений точки А. Действительно, если то конец ускорения обязательно находится на этой прямой, а если , то конец ускорения находится с той стороны этой прямой, где расположен полюс.

Следствие 2. Концы ускорений точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между этими точками.

Зная ускорение точки А отрезка АВ, алгебраические величины угловой скорости и углового ускорения , определим ускорение точки В отрезка, приняв точку А за полюс:

.

Рис. 11.11

Построим в точке В ускорение полюса (рис. 11.11). Положим, что отрезок вращается ускоренно в направлении, обратном направлению вращения часовой стрелки. Из конца ускорения отложим ускорение под углом к отрезку A₁b, равному и параллельному отрезку АВ. Соединив точку В с концом , получаем ускорение точки В.

Для определения ускорения какой-либо другой точки отрезка, на­пример точки D, выполним аналогичное построение.

Очевидно, что ускорение составляет с отрезком А₁b тот же угол β.

Ускорения точек В и D отрезка в его вращательном движении вокруг полюса А пропорциональны расстояниям от этих точек до полюса. Действительно,

Поэтому dD₁/bB₁= AD/AB, но AD=A₁d и АВ=А₁b, как противопо­ложные стороны параллелограммов. Тогда

.

Таким образом, . Из подобия треугольников следует, что:

Концы ускорений - точки a₁, d₁ и В₁ - лежат на oдной прямой;

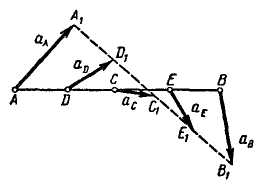
Рис. 11.12

Последнее соотношение показывает, что концы ускорений точек неизменяемого отрезка делят прямую, соединяющую эти концы, на части, пропорциональные расстояниям между соответствующими точ­ками.

Поэтому, зная ускорения и концов отрезка АВ, можно определить графически ускорения любой точки этого отрезка.

Допустим, что требуется определить ускорение точек D, С и Е, делящих отрезок на четыре равные части (рис. 11.12). Соединяем концы ускорений точек А и В, отложенных в масштабе, отрезком прямой А₁В₁ и делим этот отрезок точками D₁, C₁ и E₁ на четыре равные части. Соединяя точки D и D₁, С и C₁, E и E₁, получаем ускорения этих точек , и . Пользуясь масштабом, находим их модули и по чертежу определяем их направления.